Reading Notes-opencv-Polar Coordinate Transformation

Principle analysis

Polar coordinate transformation is used to correct circular objects in images or to include them in circular objects.

Any point (x,y) on the xoy plane of Cartesian coordinates corresponds to the polar coordinates (theta, r) in the polar coordinate system by the following calculation formula with (x1,y1) as the center.

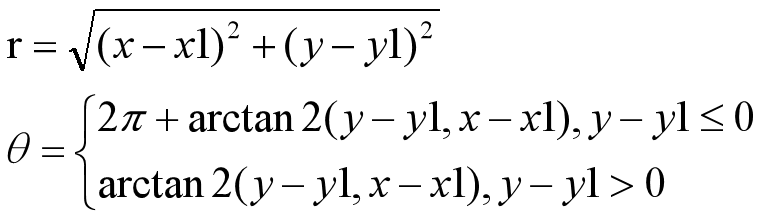
The angle range after polar coordinate transformation [0,360]

Examples: (11, 13) Polar coordinate transformation centered on (3, 5)

import math
r = math.sqrt(math.pow(11-3, 2) + math.pow(13-5, 2))
theta = math.atan2(13-5, 11-3)/math.pi*180							#Conversion to angle
print(r, theta)

opencv provides functions:

​

x = np.array([[0,1,2],[0,1,2],[0,1,2]], dtype = "float64")-1
y = np.array([[0,0,0],[1,1,1],[2,2,2]], np.float64)-1
r, theta = cv2.cartToPolar(x,y, angleInDegrees = True)
print(r, theta)

angleInDegrees = True returns the angle, and vice versa, the radian. array data types are floating-point, float32 or float64, x, y arrays of the same size and data type.

Converting polar coordinates to Cartesian coordinates

If the polar coordinates (theta, r) are known, the Cartesian coordinates (x1, y1) are taken as the center.

The original coordinates (x, y) can be expressed as:
x=x1+rcosθ,y=y1+rsinθ x = x1 + rcosθ, y = y1 + rsinθ x=x1+rcosθ,y=y1+rsinθ
opencv provides functions:

angle = np.array([[30,31], [30,31]], np.float32)
radiu = np.array([[10,10], [11, 11]], np.float32)
x, y = cv2.polarToCart(radiu, angle, angleInDegrees = True )

C++ implementation:

Mat angle = (Mat_<float>(2,2) << 30, 31, 30, 31);
Mat radiu = (Mat_<float>(2,2) << 10, 10, 11, 11);
Mat x, y;
polarToCart(radiu, angle, x, y, true);

Function parameters are similar to the previous Python.

Image transformation using polar coordinate transformation

Suppose that the input matrix bit I, (x1, y1) represents the center of the polar coordinate transformation, and the output image matrix bit O. The polar coordinates correspond to the Cartesian coordinate system one-to-one.
O(I,θ)=fI(x1+rcosθ,y1+rsinθ) O(I, θ) = f_{I}(x_{1} + rcosθ, y_{1} + rsinθ) O(I,θ)=fI​(x1​+rcosθ,y1​+rsinθ)
Here I and theta are all in step 1, and the output matrix may be seriously distorted. It is improved by assuming that the distance range of (x1, y1) [r min, R max], the angle range [theta min, theta max] are coordinates and transformed to discretize; assuming that the transformation step of R is rstep, 0 < RStep <= 1, and theta is theta step, generally 360/(180*N), N >= 2, and the width of the output matrix is w ~ (rmax - rmin)/r step + 1, high h.~ (Theta max-Theta min)/Theta step+1. The value of column j in row I of image matrix O is:
O(i,j)=fI(x1+(rmin+rstep∗i)∗cos(θmin+θstep∗j),y1+(rmin+rstep∗i)∗sin(θmin+θstep∗j)) O(i,j) = f_{I}(x_{1} + (r_{min} + r_{step} * i)*cos(θ_{min} + θ_{step} *j), y_{1} + (r_{min} + r_{step} * i)*sin(θ_{min} + θ_{step} *j)) O(i,j)=fI​(x1​+(rmin​+rstep​∗i)∗cos(θmin​+θstep​∗j),y1​+(rmin​+rstep​∗i)∗sin(θmin​+θstep​∗j))
Code implementation:

import cv2
import numpy as np 
import sys
import math 

def polar(I, center, r, theta= (0,360), rstep = 1.0, thetastep = 360.0/(180*8)):
	#Get the range of minimum and maximum distance
	minr, maxr = r
	#Get the minimum and maximum range of angle
	mintheta, maxtheta = theta
	#
	H = int((maxr - minr) / rstep) +1
	W = int((maxtheta - mintheta) / thetastep) +1
	O = 125 * np.ones((H, W), I.dtype)

	#tile(a,(2,3)) replicates 2,3 times in vertical and horizontal directions
	

	#numpy.linspace(start, stop[, num=50[, endpoint=True[, retstep=False[, dtype=None]]]]])
	#Returns a uniformly spaced number (an array) within a specified range, that is, an array of equals and equals.
	#start - start, stop - End, num - Number of Elements, default is 50,
	#endpoint - Does it contain a stop value, which defaults to True and contains a stop value; if it is False, it does not contain a stop value?
	#retstep - The return value form, default to False, returns an array of equal-difference arrays, and if True, returns the result (array ([`samples', `step').)
	#dtype - The data type returned by default is not available, if not, refer to the input data type.

	#For details on the use of transpose, see https://blog.csdn.net/xiongchengluo1129/article/details/79017142

	#Polar coordinate transformation
	r = np.linspace(minr,maxr,H)			
	r = np.tile(r,(W,1))
	r = np.transpose(r)
	theta = np.linspace(mintheta,maxtheta,W)
	theta = np.tile(theta,(H,1))
	x,y=cv2.polarToCart(r,theta,angleInDegrees=True)


	#Nearest neighbor interpolation
	for i in range(H):
		for j in range(W):
			px = int(round(x[i][j])+cx)
			py = int(round(y[i][j])+cy)
			if((px >= 0 and px <= w-1) and (py >= 0 and py <= h-1)):
				O[i][j] = I[py][px]
			else:
				O[i][j] = 125#gray
	return O
    
#Main function
if __name__ == "__main__":
	imagePath = "G:\\blog\\OpenCV_picture\\chapter3\\img2.jpg"  #"G: blog OpenCV algorithm refinement - Test picture Chapter 3 image2.jpg"
	image = cv2.imread(imagePath, cv2.IMREAD_GRAYSCALE)
	
    #Width and Height of Image
	h,w = image.shape[:2]
	print (w,h)
    #The Center of Extremely Left Scale Transform
	cx,cy = 508,503
	print (cx,cy)
	cv2.circle(image,(int(cx),int(cy)),10,(255.0,0,0),3)
    #Minimum and Maximum Radius of Distance #200 550 270,340
	O = polar(image,(cx,cy),(0,550))
    #rotate
	O = cv2.flip(O,0)
    #Display the original image and output image
	cv2.imshow("image",image)
	cv2.imshow("O",O)
	cv2.imwrite("O.jpg",O)
	cv2.waitKey(0)
	cv2.destroyAllWindows()

Note: xrange () is merged into range () in opencv3

C++ Implementation

First, we introduce the repeat () function, which is similar to the previous tile () function.

void repeat(const Mat& sr, int ny, int nx)

Input matrix of src, ny repeats SRC nytimes vertically and nx repeats SRC nx times horizontally.

Through polar () function and coordinate transformation, parameter I is the input image, center is more than a dozen coordinate transformation centers, minr is the smallest distance from the transformation center, mintheta is the smallest angle, thetaStep is the angle transformation step, rStep is the distance transformation step, interpolation uses the nearest interpolation algorithm.

Mat polar(Mat I, Point2f center, Size size, float minr = 0, float mintheta = 0.0, float thetaStep = 1.0 / 4, float rStep = 1.0)
{
	//Constructing Radius Matrix
	Mat r_i = Mat::zeros(Size(1, size.height), CV_32FC1);
	for (int i = 0; i < size.height; i++)
	{
		r_i.at<float>(i, 0) = minr + i * rStep;
	}
	Mat r = repeat(r_i, 1, size.width);

	//Constructing Angle Matrix
	Mat theta_j = Mat::zeros(Size(size.width, 1), CV_32FC1);
	for (int j = 0; j < size.height; j++)
	{
		theta_j.at<float>(0, j) = mintheta + j * thetaStep;
	}
	Mat theta = repeat(theta_j, size.height, 1);

	//Converting polar coordinates into Cartesian coordinates
	Mat x, y;
	polarToCart(r, theta, x, y, true);
	//Move the coordinate center to the origin
	x += center.x;
	y += center.y;

	//Nearest neighbor interpolation
	Mat dst = 125 * Mat::ones(size, CV_8UC1);
	for (int i = 0; i < size.height; i++)
	{
		for (int j = 0; j < size.width; j++)
		{
			float xij = x.at<float>(i, j);
			float yij = y.at<float>(i, j);
			int nearestx = int(round(xij));
			int nearesty = int(round(yij));
			if ((0 <= nearestx && nearestx < I.cols) && (0 <= nearesty && nearesty < I.rows))
			{
				dst.at<uchar>(i, j) = I.at<uchar>(nearestx, nearesty);
			}
		}
	}

	return dst;

}

int main()
{
	std::string iamge_path = "G:\\blog\\OpenCV_picture\\chapter3\\img2.jpg";
	Mat image = imread(iamge_path, 0);

	if (!image.data)
	{
		return -1;
	}

	//Image Polar Coordinate Change
	float thetaStep = 1.0 / 4;
	float minr = 270;
	Size size(int(360 / thetaStep), 70);
	Mat dst = polar(image, Point2f(508, 503), size, minr);


	//Horizontal Direction Mirror Processing
	flip(dst, dst, 0);

	//display
	imshow("I", image);
	imshow("polar: ", dst);
	waitKey(0);

	return 0;
}

Results:

void filp(InputArray src, OutputArray dst, int flipCode)

FlpCode: > 0:src mirror processing around y axis

Image Processing of 0:src Around x-axis

The <0:src rotates 180 degrees counter-clockwise, first around the x-axis and then around the y-axis.

The geometric transformation of flip() function is not by affine transformation, but by row-column interchange, declared in core.hpp.

Linear Polar Function

​

void linearPolar(InutArray src, OutputArray dst, Point2f center, double maxRadius, int flags)

Center: Polar coordinate transformation center; maxRadius: maximum distance of polar coordinate transformation, flags: interpolation algorithm, similar to resize() and warpAffine() in the previous paper.

Code implementation:

int main()
{
	std::string iamge_path = "G:\\blog\\OpenCV_picture\\chapter3\\img2.jpg";
	Mat image = imread(iamge_path, 0);

	if (!image.data)
	{
		return -1;
	}

	Mat dst;
	linearPolar(image, dst, Point2f(508, 503), 550, CV_INTER_CUBIC);
	//This is not a nearest neighbor interpolation algorithm.

	imshow("InitImage", image);
	imshow("PolarImage", dst);

	waitKey(0);
	return 0;

}

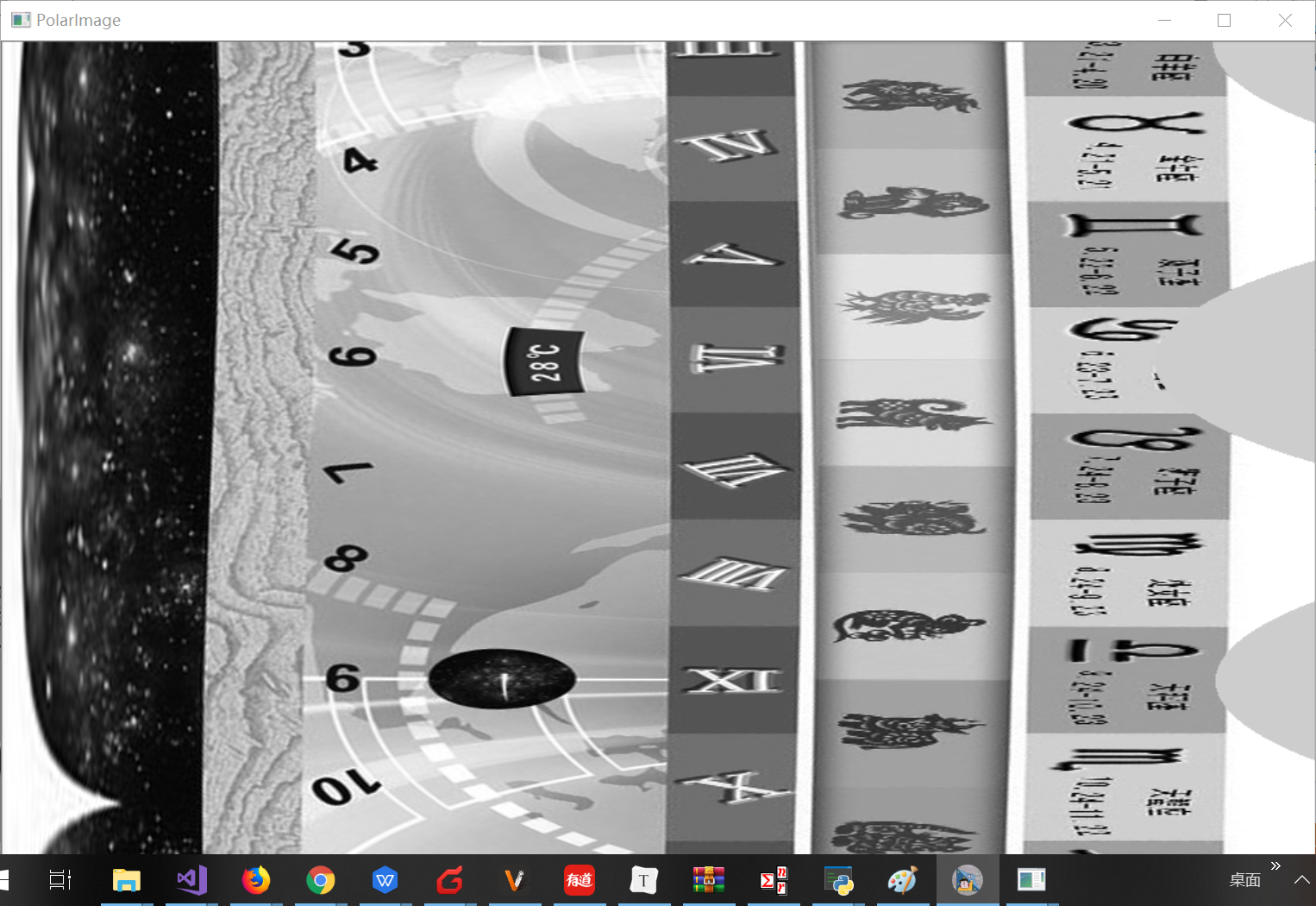
The function has two shortcomings: the step of polar coordinate transformation is uncontrollable, and it can only transform the whole region of the circle, not the circle.

void logPolar (InutArray src, OutputArray dst, Point2f center, double maxRadius, int flags)

This function is similar to the linearPolar () function.