Quick sort

  in other words, it's called fast platoon, but it will become slow platoon under certain circumstances. OK, OK, enter the text

Fast platoon also adopts a divide and conquer strategy. The basic idea of this method is:

• 1. Find a base number first. I usually use the first number
• 2. Then, the left side of the square smaller than the cardinal number and the right side of the square larger than the cardinal number are divided into left and right intervals with the lower side of the cardinal number as the dividing line
• 3. Then repeat the operation in the left and right sections
• 4. Finally, we will get n ordered intervals

Just give an example

Now there is an unordered array arr 👇

We now take the first element as the base, that is, pivot=arr[0] = 77, the left subscript is 0, the right subscript is 7, and now the subscript is 0, which is a radish pit waiting for others to fill in 👇

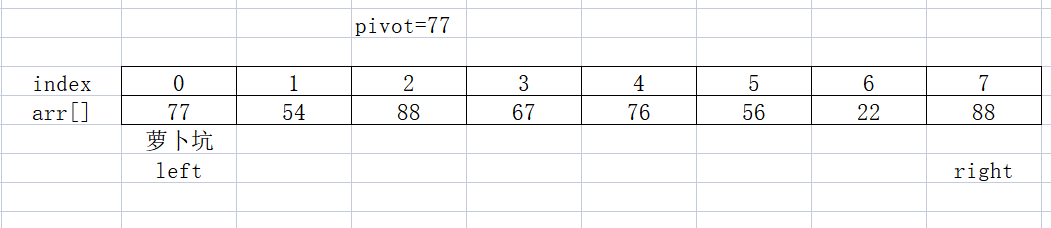
Now scan from the right to the left to find the first number smaller than pivot. Walk, walk, find it. It's unlucky when right = 6. Ha ha, now arr[left++] = arr[right]. Well, now the radish pit is filled by arr[6], but there is another pit (arr[6]). What should I do? 👇

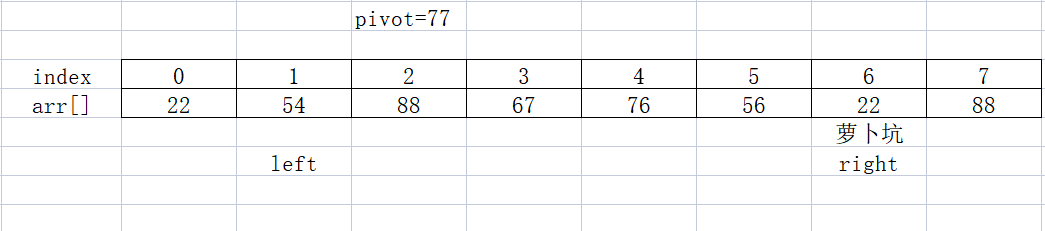
Just scan from the right. Now scan from the left to find a number larger than the base pivot. Look who's unlucky. Go, go, hey, find it again. arr[2] this young man is unlucky. Well, now, according to the old rule, fill the pit arr [right --] = arr [left]. Now the pit on the right is filled, and there's another pit on the left. The program apes take a detour when they see it.

Continue. Scan the number smaller than pivot from the right. arr[5] Unfortunately, it won the prize. It's going to fill the pit. arr[left++] =arr[right], 👇

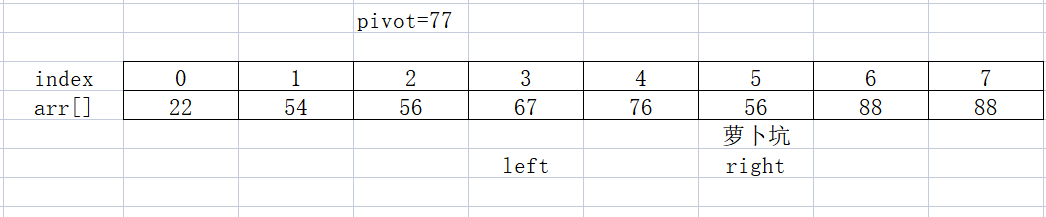
Now the routine should be familiar, and start scanning the number larger than the pivot from the left. Unfortunately, left went to the pit and didn't find it. Now I can only throw the pivot into the pit 👇

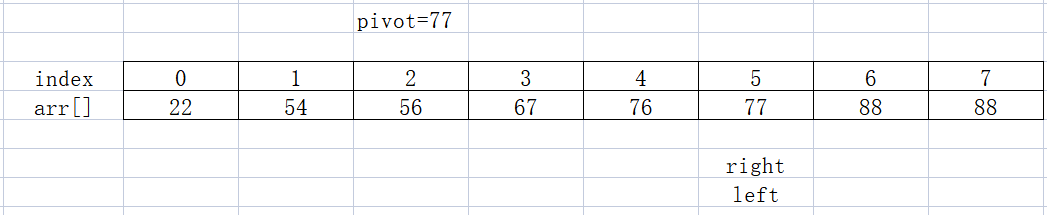
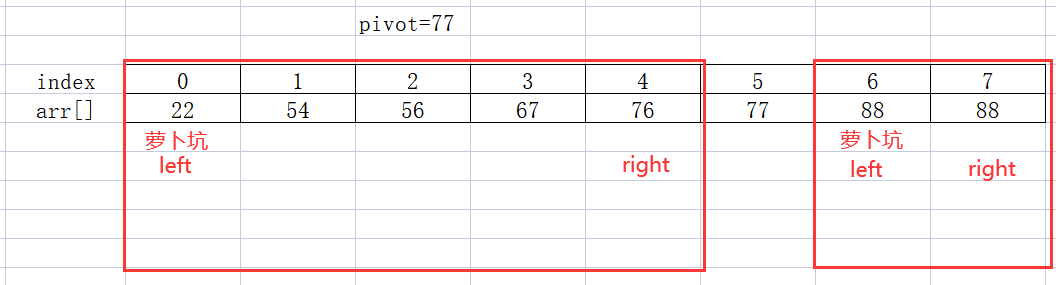
Now mark 5 as the dividing line, start zoning, and repeat the operation above...
Partition: 👇

Code demonstration

/**
 * Quick sorting 100 W pieces of data with an average of 0.143 S
 */
public class QuickSort {
    /**
     * entrance
     *
     * @param arr Array to be sorted
     */
    private static void quickSort(int[] arr) {
        quickSort(arr, 0, arr.length - 1);
    }

    /**
     * heavy load
     *
     * @param arr        Array to be sorted
     * @param startIndex Start boundary subscript
     * @param endIndex   End boundary subscript
     */
    private static void quickSort(int[] arr, int startIndex, int endIndex) {
        if (startIndex >= endIndex) { //Recursive end condition
            return;
        }
        int pivotIndex = fillThePit(arr, startIndex, endIndex);
        quickSort(arr, startIndex, pivotIndex - 1);
        quickSort(arr, pivotIndex + 1, endIndex);
    }

    /**
     * Radish pit filling
     *
     * @return Returns the subscript of the last pit
     */
    private static int fillThePit(int[] arr, int startIndex, int endIndex) {
        int left = startIndex;
        int right = endIndex;
        int pivot = arr[startIndex];
        while (left < right) {
            while (left < right && arr[right] > pivot) { // Find the first number less than pivot from right to left
                right--;
            }
            if (left < right) { //Fill the pit and generate a new pit arr[right]
                arr[left++] = arr[right];
            }
            while (left < right && arr[left] < pivot) { // Find the first number greater than or equal to pivot from left to right
                left++;
            }
            if (left < right) { //Fill the pit and generate a new pit arr[left]
                arr[right--] = arr[left];
            }
        }
        //Fill the base number in the last hole left unattended
        arr[right] = pivot;
        return left;
    }

    public static void main(String[] args) {
        Random random = new Random();
        int[] arr = new int[1000000];
        for (int i = 0; i < 1000000; i++) {
            int num = random.nextInt(3000000);
            arr[i] = num;
        }
        long start = System.currentTimeMillis();
        quickSort(arr);
        long end = System.currentTimeMillis();
        System.out.println((end - start) / 1000.0);
    }
}