Quick Sorting of Data Structures

demo : http://download.csdn.net/detail/keen_zuxwang/9879425

Quick sort
It is a very efficient sorting algorithm, which moves the record with larger keywords from the front to the back directly, and the record with smaller keywords from the back to the front directly, thus reducing the total number of comparisons and moves.
It uses the idea of "divide and conquer", dividing large arrays into small arrays based on benchmarks, and small ones into smaller ones until the elements of the array are one.

Sorting Thought:
For a given set of records, select a base element (usually the first or last element).
Through one scan, the column to be sorted is divided into two parts, one is smaller than the base element, and the other is larger than or equal to the base element (at this time, the correct position of the base element after its ordering).
Then, the two parts are sorted recursively in the same way until all records in the sequence are in order.

Algorithmic stability
Quick sort is not stable, because there is data exchange, it can not guarantee that the same data is scanned and stored in order.

Scenarios for Algorithmic Application
Quick sort is applicable in most cases, especially in the case of large amount of data.

Time complexity:
Worst-case time complexity: O(n^2)
The worst case is that the result of each interval division is that the left (or right) sequence of benchmark keywords is empty, while the record in the other interval is only one item less than that before sorting, that is, the selected keyword is the minimum or maximum value of the record to be sorted.
Best time complexity: O(nlogn)
The best case is that the result of each interval division is that the left and right sides of the benchmark keyword are equal or the difference is 1, that is, the selected benchmark keyword is the intermediate value of the record to be sorted. At this time, the total number of comparisons is nlogn.
Average time complexity: O(nlogn)
Among the algorithms with O(nlogn) average time complexity, the average performance of fast sorting is the best.

Spatial complexity
A stack space is needed to implement recursion in the process of quick sorting.
In the best case, the depth of the recursive tree is log2n, and its spatial complexity is O(nlogn).
In the worst case, n-1 recursion is needed, and its spatial complexity is O(n).
In the average case, the spatial complexity is O(nlogn).

Selection of benchmark keywords (the key to fast sorting algorithm):
The first one is to choose the three. Comparing the records at the beginning, the end and the middle of the sequence, the median of the three is chosen as the base keyword.
The second is to take a random number between left and right and write a picture description here, using n[m] as the base keyword. The quick sorting obtained by this method is generally called random quick sorting.

import java.util.Arrays;
import java.util.Stack;

public class QuickSort {
  private static int num=0;
  private static Stack<Integer> stack = new Stack<Integer>();  

  public static int partition(int[] arr, int left, int right) {
      int pivotKey = arr[left];
      int pivotPointer = left;
      num++;
      System.out.println("------------------num = "+num+"------------------");
      System.out.println("left = "+left +" right = "+right +" key = "+ pivotKey);
      System.out.println(Arrays.toString(arr));
      while (left < right) {
          while (left < right && arr[right] >= pivotKey)
              right--;
          while (left < right && arr[left] <= pivotKey)
              left++;
          System.out.println("left = "+left +" right = "+right);
          swap(arr, left, right);// Switch the big ones to the right and the small ones to the left.
          System.out.println(Arrays.toString(arr));
      }
      swap(arr, pivotPointer, left);// Finally, pivot is swapped to the middle.
      System.out.println("\n"+Arrays.toString(arr));
      System.out.println();
      return left;

  }

  private static void swap(int[] arr, int left, int right) {
      int temp = arr[left];
      arr[left] = arr[right];
      arr[right] = temp;

  }

  //Recursion and partition
  public static void quickSort(int[] arr, int left, int right) {
      if (left < right) {
         int pivotPos = partition(arr, left, right);
         quickSort(arr, left, pivotPos - 1);
         quickSort(arr, pivotPos + 1, right);
      }
  }

  //non-recursive
  public static void stackSort(int[] items, int l, int r) {  
      int i;  
      push(r, l); //Push r and l into the stack  

      while(!stackempty()) { //As long as the stack is not empty, it keeps looping  
          l = pop(); 
          r = pop();  
          if(r <= l) 
              continue;  
          i = partition(items, l, r);  
          //The larger side is first stacked, which ensures that the maximum depth of the stack is within lgN.  
          if(i-l > r-i) {  
              push(i-1, l); 
              push(r, i+1);  
          } else {  
              push(r, i+1); 
              push(i-1, l);  
          }  
      }  
  }  

  //Push a and b into the stack in turn  
  private static void push(int a, int b) {  
      stack.push(a);  
      stack.push(b);  
  }  

  private static boolean stackempty() {  
      return stack.isEmpty();  
  }  

  private static int pop() {  
      return stack.pop();  
  }

  public static void quickSort1(int[] items, int l, int r) {  
      if(l >= r) return; //No sort  

      swap(items, (l+r)/2, r-1);  
      compexch(items, l, r-1);  
      compexch(items, l, r);  
      compexch(items, r-1, r);  
      //After the above three steps, the sorting of l, (l+r)/2 and R is completed. ((l+r)/2 element in r-1 position) => base keyword, three in the middle

      //Un l ike ordinary quick sorting, the first and r are not considered when partitioning.  
      //Because the first element must be smaller than the "flag (pivot) element" and the r element must be larger than the "flag (pivot) element".  
      //"Flag (pivot) element" on r-1.  
      int i = partition(items, l+1, r-1);  

      quickSort1(items, l, i-1); //Recursive Sorting  
      quickSort1(items, i+1, r); //Recursive Sorting  
  }

  private static void compexch(int[] items, int a, int b) {  
      if(items[b] < items[a]) { 
         swap(items, a, b);  
      }
  } 

  public static void main(String[] args) {
      int[] a = { 49, 38, 65, 97, 76, 13, 27, 49 }; 
      int[] b = { 49, 38, 65, 97, 76, 13, 27, 49 };
      int[] c = { 49, 38, 65, 97, 76, 13, 27, 49 };

      /*
      System.out.println("Before sorting: ";
      System.out.println(Arrays.toString(a));

      stackSort(a, 0, a.length - 1); 

      System.out.println("After sorting: ";
      System.out.println(Arrays.toString(a));
      */

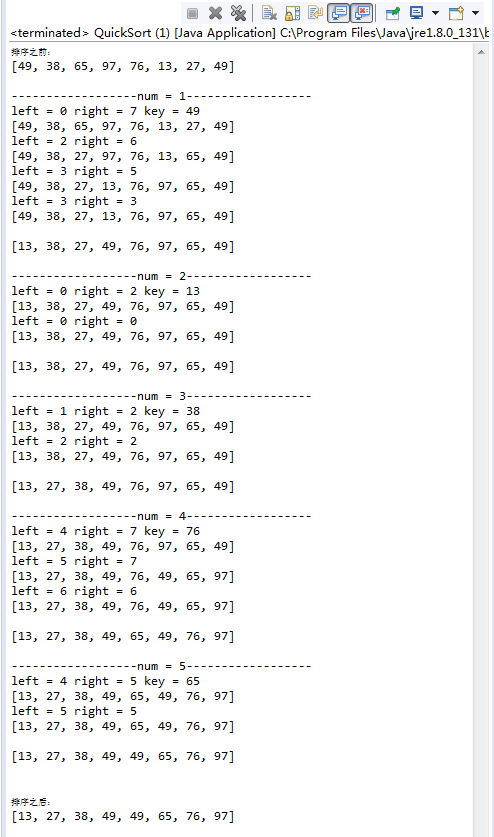
      System.out.println("Before sorting:");
      System.out.println(Arrays.toString(b));
      System.out.println();

      //Quick sort
      quickSort1(b, 0, b.length - 1);
      System.out.println();

      System.out.println("After sorting:");
      System.out.println(Arrays.toString(b));

      /*
      System.out.println("Before sorting: ";
      System.out.println(Arrays.toString(b));
      System.out.println();

      //Quick sort
      quickSort(b, 0, b.length - 1);
      System.out.println();

      System.out.println("After sorting: ";
      System.out.println(Arrays.toString(b));
      */
  }
}