QTREE5

Operation: reverse the color of a point, query the nearest white point of a point

We maintain the distance from the shallowest node to the nearest white point (lsum) and the distance from the deepest node to its nearest white point (rsum) in Splay.

So the answer to query x is obviously Accss (x), splay (x), X - > Rsum.

Consider how to push up

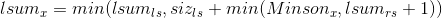
Minson is a virtual subtree answer, maintained with a set

#include<bits/stdc++.h>
#define N 100050
using namespace std;
int read(){
	int cnt = 0; char ch = 0;
	while(!isdigit(ch)) ch = getchar();
	while(isdigit(ch)) cnt = cnt*10 + (ch-'0'), ch = getchar();
	return cnt;
}
const int inf = 0x3fffffff;
vector<int> v[N];
int n, m, col[N];
int ch[N][2], fa[N], siz[N], lsum[N], rsum[N];
multiset <int> S[N]; 
void dfs(int u, int f){
	for(int i=0; i<v[u].size(); i++){
		int t = v[u][i]; if(t == f) continue;
		fa[t] = u; S[u].insert(inf + 1); dfs(t, u);
	} 
}
#define ls ch[x][0]
#define rs ch[x][1]
bool isRoot(int x){ return ch[fa[x]][0] != x && ch[fa[x]][1] != x;}
int Top(int x){ if(S[x].empty()) return inf; return *S[x].begin();}
void Pushup(int x){
	if(!x) return; lsum[x] = rsum[x] = inf;
	siz[x] = siz[ls] + siz[rs] + 1;
	lsum[x] = min(lsum[ls], siz[ls] + min(col[x] ? 0 : inf, min(Top(x), lsum[rs] + 1)));
	rsum[x] = min(rsum[rs], siz[rs] + min(col[x] ? 0 : inf, min(Top(x), rsum[ls] + 1)));
}
void rotate(int x){
	int y = fa[x], z = fa[y], k = ch[y][1] == x;
	if(!isRoot(y)) ch[z][ch[z][1] == y] = x; fa[x] = z;
	ch[y][k] = ch[x][k^1]; fa[ch[x][k^1]] = y;
	ch[x][k^1] = y; fa[y] = x; Pushup(y); Pushup(x);
}
void Splay(int x){
	while(!isRoot(x)){
		int y = fa[x], z = fa[y];
		if(!isRoot(y)) rotate((ch[y][0] == x) ^ (ch[z][0] == y) ? x : y);
		rotate(x);
	}
}
void Access(int x){
	for(int y = 0; x; y = x, x = fa[x]){
		Splay(x); 
		if(rs) S[x].insert(lsum[rs] + 1);
		rs = y;
		if(rs) S[x].erase(S[x].find(lsum[rs] + 1));
		Pushup(x);
	}
}
int main(){
	n = read(); lsum[0] = rsum[0] = inf;
	for(int i=1; i<n; i++){
		int x = read(), y = read();	
		v[x].push_back(y); v[y].push_back(x); 
	} dfs(1, 0);
	m = read();
	while(m--){
		int op = read(), x = read();
		if(op == 0){ Access(x); Splay(x); col[x] ^= 1; Pushup(x);}
		if(op == 1){ Access(x); Splay(x); printf("%d\n", (rsum[x] == inf) ? -1 : rsum[x]);}
	} return 0;
}

QTREE6 

Operation: reverse color, query the size of connected blocks of the same color

First, open two LCT s, reverse color is equivalent to violent Cut and violent Link on one side

We consider only Cut x and its fa, also Link x and its fa. Such a connected block only has the possibility that rt is different from its color, so it's better to judge specially.

And then there's the Siz that maintains the virtual subtree.

#include<bits/stdc++.h>
#define N 1000050
using namespace std;
int read(){
	int cnt = 0; char ch = 0;
	while(!isdigit(ch)) ch = getchar();
	while(isdigit(ch)) cnt = cnt*10 + (ch-'0'), ch = getchar();
	return cnt;
}
int first[N], nxt[N], to[N], tot;
void add(int x, int y){ nxt[++tot] = first[x], first[x] = tot, to[tot] = y;}
int n, m, col[N];
struct LCT{
	struct Node{ int ch[2], fa, siz; } t[N];
	int si[N];
	#define ls t[x].ch[0] 
	#define rs t[x].ch[1]
	bool isRoot(int x){ int fa = t[x].fa; return t[fa].ch[0] != x && t[fa].ch[1] != x; }
	void Pushup(int x){ t[x].siz = t[ls].siz + t[rs].siz + si[x] + 1;}
	void rotate(int x){
		int y = t[x].fa, z = t[y].fa, k = t[y].ch[1] == x;
		if(!isRoot(y)) t[z].ch[t[z].ch[1] == y] = x; t[x].fa = z;
		t[y].ch[k] = t[x].ch[k^1]; t[t[x].ch[k^1]].fa = y;
		t[x].ch[k^1] = y; t[y].fa = x; Pushup(y); Pushup(x);
	}
	void Splay(int x){
		while(!isRoot(x)){
			int y = t[x].fa, z = t[y].fa;
			if(!isRoot(y)) rotate((t[y].ch[0] == x) ^ (t[z].ch[0] == y) ? x : y);
			rotate(x);
		} Pushup(x);
	}
	void Access(int x){
		for(int y=0; x; y=x, x=t[x].fa){ 
			Splay(x);
			si[x] += t[rs].siz;
			rs = y;
			si[x] -= t[rs].siz;
			Pushup(x);
		} 
	}
	void Link(int x, int y){ 
		if(!y) return;
		Access(y); Splay(y); Splay(x); t[x].fa = y; si[y] += t[x].siz; Pushup(y); 
	}
	void Cut(int x, int y){
		if(!y) return;
		Access(x); Splay(x); t[ls].fa = 0; ls = 0; Pushup(x);
	}
	int Findroot(int x){
		Access(x); Splay(x);
		while(ls) x = ls; Splay(x);
		return x; 
	}
	int Quary(int x){
		int c = col[x]; x = Findroot(x);
		return col[x] == c ? t[x].siz : t[rs].siz;
	}
}lct[2]; 
int fa[N];
void dfs(int u, int f){
	for(int i=first[u];i;i=nxt[i]){
		int t = to[i]; if(t == f) continue;
		fa[t] = u; lct[0].Link(t, u); dfs(t, u);
	}
}
int main(){
	n = read();	
	for(int i=1; i<n; i++){
		int x = read(), y = read();
		add(x, y); add(y, x);
	} dfs(1, 0); m = read();
	while(m--){
		int op = read(), x = read();
		if(op == 0) printf("%d\n", lct[col[x]].Quary(x));
		if(op == 1){ lct[col[x]].Cut(x, fa[x]); col[x] ^= 1; lct[col[x]].Link(x, fa[x]);}
	} return 0;
}

QTREE7 

Similar to the previous question, maintain the maximum value of homochromatic connected block, multiset is OK.

#include<bits/stdc++.h>
#define N 200050
using namespace std;
int read(){
	int cnt = 0, f = 1; char ch = 0;
	while(!isdigit(ch)){ ch = getchar(); if(ch == '-') f = -1;}
	while(isdigit(ch)) cnt = cnt*10 + (ch-'0'), ch = getchar();
	return cnt * f;
}
int first[N], nxt[N], to[N], tot;
void add(int x, int y){nxt[++tot] = first[x], first[x] = tot, to[tot] = y;}
int n, m, col[N], f[N], w[N];
struct Node{
	int ch[N][2], fa[N], Max[N];
	multiset<int> S[N];
	bool isRoot(int x){ return ch[fa[x]][0] != x && ch[fa[x]][1] != x;}
	void Pushup(int x){
		Max[x] = max(w[x], max(Max[ch[x][0]], Max[ch[x][1]]));
		if(S[x].size()) Max[x] = max(Max[x], *S[x].rbegin());
	}
	void rotate(int x){
		int y = fa[x], z = fa[y], k = ch[y][1] == x;
		if(!isRoot(y)) ch[z][ch[z][1] == y] = x; fa[x] = z;
		ch[y][k] = ch[x][k^1]; fa[ch[x][k^1]] = y;
		ch[x][k^1] = y; fa[y] = x; Pushup(y); Pushup(x);
	}
	void Splay(int x){
		while(!isRoot(x)){
			int y = fa[x], z = fa[y];
			if(!isRoot(y)) rotate((ch[y][1]==x) ^ (ch[z][1]==y) ? x : y);
			rotate(x); 
		} Pushup(x);
	}
	void Access(int x){
		for(int y = 0; x; y = x, x = fa[x]){
			Splay(x); 
			if(ch[x][1]) S[x].insert(Max[ch[x][1]]);
			ch[x][1] = y; 
			if(ch[x][1]) S[x].erase(Max[ch[x][1]]);
			Pushup(x);
		}
	}
	int Findroot(int x){
		Access(x); Splay(x); while(ch[x][0]) x = ch[x][0]; Splay(x); return x;
	}
	void Link(int x, int y){
		if(!y) return;
		Access(y); Splay(y); Splay(x);
		fa[x] = y; S[y].insert(Max[x]); Pushup(y);
	}
	void Cut(int x, int y){
		if(!y) return;
		Access(x); Splay(x); fa[ch[x][0]] = 0; ch[x][0] = 0; Pushup(x);
	}
	int Quary(int x){
		int c = col[x]; x = Findroot(x);
		return col[x] == c ? Max[x] : Max[ch[x][1]];
	}
	void Modify(int x){
		Access(x); Splay(x); w[x] = read(); Pushup(x);
	}
}T[2];
void dfs(int u, int ff){
	for(int i=first[u];i;i=nxt[i]){
		int t = to[i]; if(t == ff) continue;
		T[col[t]].Link(t, u); f[t] = u; dfs(t, u); 
	}
}
int main(){
	n = read();
	for(int i=1; i<n; i++){
		int x = read(), y = read();
		add(x, y); add(y, x);
	} 
	for(int i=1; i<=n; i++) col[i] = read();
	for(int i=1; i<=n; i++) w[i] = read();
	T[0].Max[0] = T[1].Max[0] = -2e9;
	dfs(1, 0); m = read();
	while(m--){
		int op = read(), u = read();
		if(op == 0) printf("%d\n", T[col[u]].Quary(u));
		if(op == 1){ T[col[u]].Cut(u, f[u]); col[u] ^= 1; T[col[u]].Link(u, f[u]);}
		if(op == 2){ T[col[u]].Modify(u);}
	} return 0;
}