background
CNN is the top priority of deep learning, and conv1D, conv2D, and conv3D are the core of CNN, so understanding the working principle of conv becomes particularly important. In this blog, I will briefly review these three convolutions and the application methods in PyTorch.
Reference resources
https://pytorch.org/docs/master/nn.html#conv1d
https://pytorch.org/docs/master/nn.functional.html#conv1d
File
The main content of this section is to use code validation while reading the document. In PyTorch, there are conv1d, conv2d and conv3d in torch.nn and torch.nn.functional modules respectively. In terms of calculation process, there is no big difference between them. But in torch.nn, the parameters of layer and conv are obtained through training. In torch.nn.functional, they are all functions, and their parameters can be set artificially. In the analysis of this paper, the documents of the two are viewed together, but the experiment is mainly based on torch.nn.functional, which is more convenient to modify.
conv1d
Since conv parameters are almost the same, but conv1d is more convenient to understand (easier to visualize), so I will spend a lot of time to introduce this convolution method in detail.
torch.nn.functional.conv1d(input, weight, bias=None, stride=1, padding=0, dilation=1, groups=1)
input
Input is one-dimensional input, with the shape of (batch size, in channel, Length); batch size is the size of training batch; in channel is the number of input channels; Length is the Length of input, because it is one-dimensional input, it has only Length. The following figure shows a one-dimensional input consisting of three channels: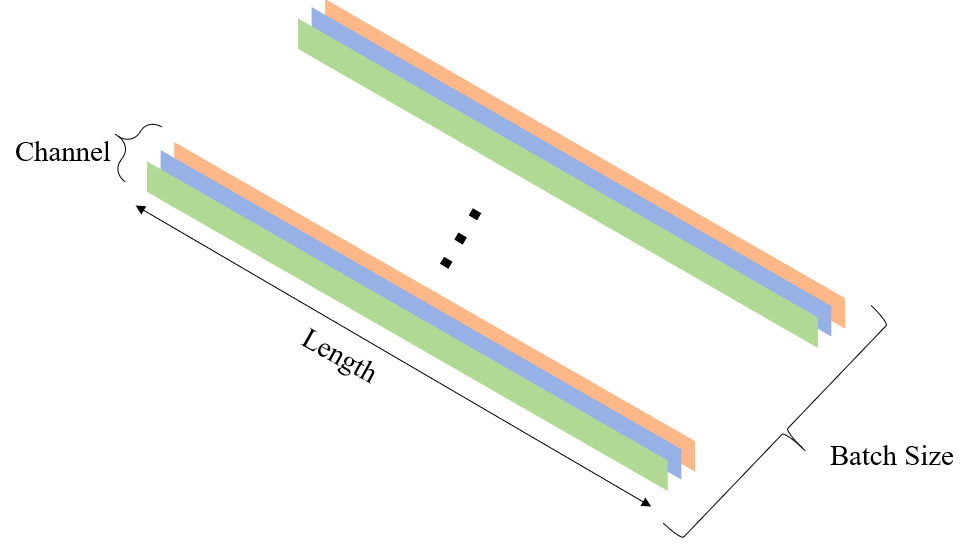
weight
weight is a one-dimensional convolution kernel, whose shape is (out channel, in channel / group, kernel size); out channel is the number of output channels; in channel / group aims to determine how the output of each layer is composed of input, which will be described in detail later. Here, Group=1 May be set; kernel size is the size of one-dimensional convolution kernel. The following figure shows a one-dimensional convolution kernel and its corresponding accumulation method: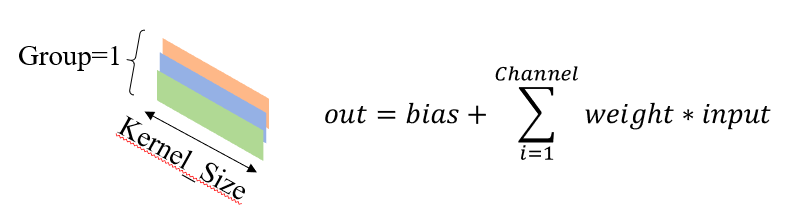
Considering that the formula is still too difficult to understand, draw another figure to show how the formula on the right side of the figure above is calculated (without drawing bias):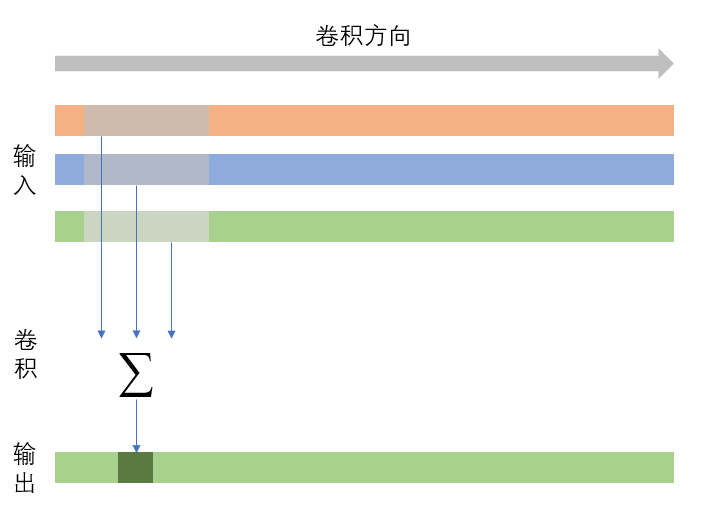
group
groups is a very special parameter in convolution, which has been mentioned before, and will be introduced in detail here. When Group=1, the output of each layer is obtained by the accumulation of all inputs and convolution kernel convolution respectively. When Group=2, the output of each layer is only obtained by the accumulation of general input volumes (it is mentioned that the number of input channels and output channels can be divided by group), and when group = in_uchannel In other words, the value of group will break the convolution relationship between input layers. Group=1 on the left and Group=3 on the right.

stride
It's easy to understand the strip. When strip = 1, the convolution kernel moves in steps of 1 on the original input; when strip = 2, the convolution kernel moves in steps of not 2; and so on. The following figure shows different convolution bands, where red represents the first convolution and purple represents the second convolution.
padding
Padding is also a very easy to understand concept, which is mainly used to deal with the boundary of convolution. For torch.nn.Conv1d, there are many modes of padding, such as setting to 0, mirroring, copying, etc.; however, torch.nn.functional.Conv1d is only set to 0.
dilation
According to my understanding, division is convolution with holes, which controls the sampling interval on the input layer. When division = 1, it is the convolution shown above. The figure below shows a case of division = 2. It is not difficult to find that this parameter can increase the receptive field without increasing the computation.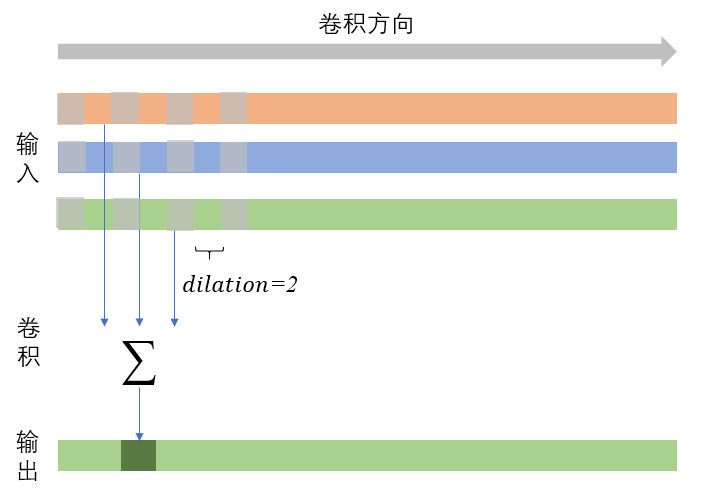
bias
bias has nothing to say.
conv2d&conv3d
In principle, if you look at the document, you will find that conv2d, conv3d and conv1d are not very different, but in terms of dimensions. Therefore, I will not introduce them separately and put them together directly. It's not hard to find that the only difference lies in the rise of dimensions; therefore, the definitions of weights are also different, namely (out ﹣ channels, groups / in ﹣ channels, KH, kW) and (out ﹣ channels, groups / in ﹣ channels, kT,kH,kW).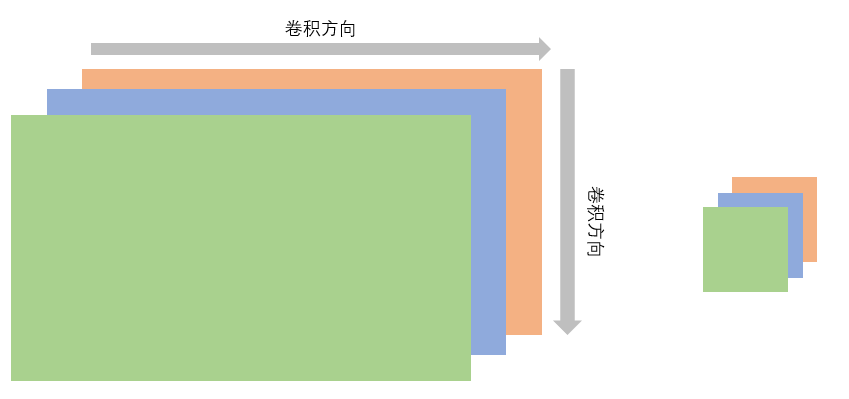

But here, I would like to add that when the input image has three RGB channels, it seems that conv2d and conv3d are no different. Anyway, all channels should be convoluted. But there is a big difference:
- conv3d can not only move the convolution on the image plane, but also convolute in the depth direction; conv2d has no such ability.
- The depth in conv3d does not correspond to the Channel in conv2d. Each depth in conv3d can correspond to multiple channels (although the figure is not drawn like this), so depth and Channel are different concepts.
Code
Write some test code below, and give a brief explanation.
conv1d
Batch_Size = 1
In_Channel = 2
Length = 7
Out_Channel = 2
Group = 1
Kernel_Size = 3
Padding = 1
Dilation = 1
one = torch.rand(Batch_Size,In_Channel,Length)
print('one',one)
# Two kernels are defined
# The first Kernel takes the middle value of the first Channel
# The second Kernel subtracts the first Channel from the second
filter = torch.zeros(Out_Channel,int(In_Channel/Group),Kernel_Size)
filter[0][0][1] = 1
filter[1][0][1] = 1
filter[1][1][1] = -1
result = F.conv1d(one,filter,padding=Padding,groups=Group,dilation=Dilation)
print('result',result)
Result
one tensor([[[0.6465, 0.3762, 0.3227, 0.6881, 0.6364, 0.5725, 0.8627],
[0.9221, 0.7417, 0.3096, 0.1008, 0.8527, 0.4099, 0.4143]]])
result tensor([[[ 0.6465, 0.3762, 0.3227, 0.6881, 0.6364, 0.5725, 0.8627],
[-0.2756, -0.3655, 0.0131, 0.5873, -0.2163, 0.1626, 0.4485]]])
conv2d
Batch_Size = 1
In_Channel = 2
Height = 5
Width = 5
Out_Channel = 2
Group = 1
Kernel_Size_H = 3
Kernel_Size_W = 3
Padding = 1
Dilation = 1
# Two kernels are defined
# The first Kernel takes the value of the upper left corner of the first Channel
# The second Kernel takes the value of the lower right corner of the second Channel
two = torch.rand(Batch_Size,In_Channel,Height,Width)
print('two',two)
filter = torch.zeros(Out_Channel,int(In_Channel/Group),Kernel_Size_H,Kernel_Size_W)
filter[0][0][0][0]=1
filter[1][1][2][2]=1
depth = F.conv2d(two,filter,padding=Padding)
print(depth.shape)
print(depth)
Result
two tensor([[[[0.6886, 0.5815, 0.2635, 0.5373, 0.2606],
[0.7335, 0.2440, 0.5123, 0.9990, 0.1864],
[0.5270, 0.1498, 0.0728, 0.1900, 0.0408],
[0.0819, 0.2725, 0.7476, 0.8551, 0.2504],
[0.2355, 0.5189, 0.7329, 0.8619, 0.3117]],
[[0.5712, 0.4581, 0.7050, 0.2502, 0.3364],
[0.1892, 0.6736, 0.3675, 0.2895, 0.8894],
[0.5782, 0.0020, 0.5400, 0.4404, 0.3508],
[0.3597, 0.1373, 0.0068, 0.0440, 0.9917],
[0.3296, 0.0371, 0.0367, 0.0597, 0.8797]]]])
torch.Size([1, 2, 5, 5])
tensor([[[[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.6886, 0.5815, 0.2635, 0.5373],
[0.0000, 0.7335, 0.2440, 0.5123, 0.9990],
[0.0000, 0.5270, 0.1498, 0.0728, 0.1900],
[0.0000, 0.0819, 0.2725, 0.7476, 0.8551]],
[[0.6736, 0.3675, 0.2895, 0.8894, 0.0000],
[0.0020, 0.5400, 0.4404, 0.3508, 0.0000],
[0.1373, 0.0068, 0.0440, 0.9917, 0.0000],
[0.0371, 0.0367, 0.0597, 0.8797, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000]]]])
conv3d
Batch_Size = 1 In_Channel = 2 Height = 5 Width = 5 Depth = 5 Out_Channel = 2 Group = 1 Kernel_Size_D = 3 Kernel_Size_H = 3 Kernel_Size_W = 3 Padding = 1 Dilation = 1 # Two kernels are defined # The first Kernel takes the value of the first depth and the upper left corner # The second Kernel does nothing thr = torch.rand(Batch_Size,In_Channel,Depth,Height,Width) print(thr) filter = torch.zeros(Out_Channel,int(In_Channel/Group),Kernel_Size_D,Kernel_Size_H,Kernel_Size_W) filter[0][0][0][0][0]=1 result = torch.conv3d(thr,filter,padding=1) print(result)
Result
tensor([[[[[0.9226, 0.8931, 0.7071, 0.7718, 0.5866],
[0.1164, 0.8881, 0.5236, 0.7025, 0.1280],
[0.1002, 0.0013, 0.1704, 0.1424, 0.5018],
[0.8796, 0.3582, 0.2792, 0.7098, 0.9759],
[0.4871, 0.3776, 0.9242, 0.5693, 0.0594]],
[[0.7816, 0.8589, 0.4025, 0.0712, 0.4381],
[0.2501, 0.1536, 0.5014, 0.4333, 0.9369],
[0.9491, 0.8624, 0.4953, 0.6443, 0.4056],
[0.7834, 0.2791, 0.5448, 0.0204, 0.4199],
[0.1179, 0.0021, 0.3744, 0.6835, 0.4836]],
[[0.9522, 0.0417, 0.0653, 0.4445, 0.2879],
[0.2581, 0.8633, 0.2610, 0.9866, 0.9338],
[0.2689, 0.6511, 0.0543, 0.7373, 0.2599],
[0.7211, 0.9832, 0.9786, 0.3957, 0.2649],
[0.3640, 0.5514, 0.6898, 0.9033, 0.2067]],
[[0.5609, 0.7697, 0.0895, 0.1205, 0.2559],
[0.7284, 0.0997, 0.3773, 0.1338, 0.9526],
[0.1489, 0.0499, 0.6159, 0.9188, 0.9630],
[0.0550, 0.0325, 0.0619, 0.2393, 0.9781],
[0.6343, 0.4791, 0.6076, 0.7346, 0.1744]],
[[0.4132, 0.2946, 0.3903, 0.6658, 0.6961],
[0.7019, 0.1594, 0.6541, 0.5868, 0.0685],
[0.7312, 0.9089, 0.8287, 0.4644, 0.3078],
[0.7363, 0.2700, 0.7368, 0.8905, 0.2089],
[0.3708, 0.5744, 0.2688, 0.7639, 0.8681]]],
[[[0.7363, 0.4299, 0.6298, 0.6484, 0.5674],
[0.9055, 0.7832, 0.7443, 0.1624, 0.6099],
[0.8624, 0.1860, 0.2237, 0.3271, 0.5107],
[0.2373, 0.6254, 0.8148, 0.3317, 0.6703],
[0.8364, 0.2029, 0.2762, 0.4807, 0.6596]],
[[0.1022, 0.9687, 0.4097, 0.9130, 0.5343],
[0.3665, 0.0765, 0.0136, 0.6457, 0.5640],
[0.3436, 0.1625, 0.8261, 0.5664, 0.7331],
[0.4402, 0.8114, 0.4218, 0.5149, 0.3197],
[0.2731, 0.3032, 0.9294, 0.9505, 0.3776]],
[[0.2852, 0.0566, 0.5607, 0.0690, 0.6652],
[0.5315, 0.5046, 0.9546, 0.5480, 0.4868],
[0.5333, 0.7227, 0.0407, 0.6066, 0.6386],
[0.5846, 0.2641, 0.0451, 0.0521, 0.8822],
[0.8929, 0.2496, 0.5646, 0.3253, 0.8867]],
[[0.3010, 0.5833, 0.6355, 0.2783, 0.4770],
[0.6493, 0.2489, 0.9739, 0.8326, 0.7717],
[0.3469, 0.9503, 0.3222, 0.4197, 0.5231],
[0.2533, 0.4396, 0.8671, 0.6622, 0.3155],
[0.0444, 0.3937, 0.0983, 0.5874, 0.6237]],
[[0.8788, 0.4389, 0.2793, 0.9504, 0.5325],
[0.4858, 0.3797, 0.3282, 0.6697, 0.5938],
[0.8738, 0.4183, 0.1169, 0.2855, 0.2764],
[0.0590, 0.4542, 0.8047, 0.1575, 0.3735],
[0.2168, 0.4904, 0.1830, 0.2141, 0.4013]]]]])
tensor([[[[[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.9226, 0.8931, 0.7071, 0.7718],
[0.0000, 0.1164, 0.8881, 0.5236, 0.7025],
[0.0000, 0.1002, 0.0013, 0.1704, 0.1424],
[0.0000, 0.8796, 0.3582, 0.2792, 0.7098]],
[[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.7816, 0.8589, 0.4025, 0.0712],
[0.0000, 0.2501, 0.1536, 0.5014, 0.4333],
[0.0000, 0.9491, 0.8624, 0.4953, 0.6443],
[0.0000, 0.7834, 0.2791, 0.5448, 0.0204]],
[[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.9522, 0.0417, 0.0653, 0.4445],
[0.0000, 0.2581, 0.8633, 0.2610, 0.9866],
[0.0000, 0.2689, 0.6511, 0.0543, 0.7373],
[0.0000, 0.7211, 0.9832, 0.9786, 0.3957]],
[[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.5609, 0.7697, 0.0895, 0.1205],
[0.0000, 0.7284, 0.0997, 0.3773, 0.1338],
[0.0000, 0.1489, 0.0499, 0.6159, 0.9188],
[0.0000, 0.0550, 0.0325, 0.0619, 0.2393]]],
[[[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000]],
[[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000]]]]])
summary
I wrote a lot for no reason, maybe I still don't understand it, but I understand the running code.

