1.Autograd (automatic gradient algorithm)

autograd is the core package of PyTorch to implement the automatic gradient algorithm mentioned earlier. Let's start by introducing the variables.

2.Variable

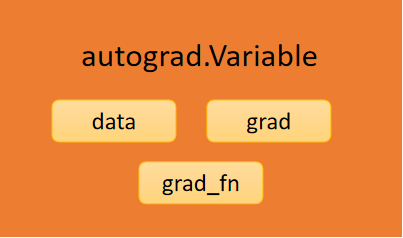
autograd.Variable is the encapsulation of Tensor. Once we have defined the final variable (i.e., calculated loss, etc.), we can call its backward() method and PyTorch will automatically calculate the gradient. As shown in the following figure, PyTorch's variable values are stored in the data, while gradient values are stored in the grad, along with a grad_fn, which is a function of calculating the gradient. In addition to user-created Tensors, variables created through Operation remember the variables it depends on to form a directed acyclic graph. When calculating the gradient of this variable, the gradient of the variable on which it depends is automatically calculated.

x = Variable(torch.ones(2, 2), requires_grad=True)

3.Gradient   (Gradient)

We can use backward() to calculate the gradient, which is equivalent to variable.backward(torch.Tensor([1.0]). The gradient passes backward and forward. The last variable is usually 1, and then the previous values are accumulated when calculating the gradient forward. PyTorch handles these things automatically and we don't need to consider them.

Note that each call to backward() calculates the gradient and adds it to the original value, so call the zero_of the variable before each call to the gradient Grad() function

import torch
from torch.autograd import Variable # Variable module in torch
x = Variable(torch.ones(2, 2), requires_grad=True)
# Parameter requires_grad indicates whether this variable is involved in calculating gradients
print(x)
y=x+2
print(y)
z = y * y * 3
print(z)
out = z.mean()# Mean
print(out)
out.backward() # Calculate all dout/dz,dout/dy,dout/dx
print(x.grad) # x.grad is dout/dx

Result:
tensor([[1., 1.],
        [1., 1.]], requires_grad=True)
tensor([[3., 3.],
        [3., 3.]], grad_fn=<AddBackward0>)
tensor([[27., 27.],
        [27., 27.]], grad_fn=<MulBackward0>)
tensor(27., grad_fn=<MeanBackward0>)
tensor([[4.5000, 4.5000],
        [4.5000, 4.5000]]
Can try, if not out.backward()，Instead of automatically calculating the gradient, the result will be None

4. Requirements_of variables Grad and volatile

Each variable has two flag s:require_ Grade and volatile, which can fine-grained control a subgraph of a computational graph without calculating gradients, can increase computational speed. An Operation requires_grad==False if all inputs do not require a gradient to be calculated Grad is False, and as long as there is one input for which a gradient needs to be calculated, the requires_of this operation Grad is TRUE. For example, the following code snippet:

import torch
from torch.autograd import Variable
x = Variable(torch.randn(5, 3))
y = Variable(torch.randn(5, 3))
z = Variable(torch.randn(5, 3), requires_grad=True)
a = x + y
print(a.requires_grad)
b = a + z
print(b.requires_grad)

False
True

If you want to fix some parameters of the model, or if you know that the gradient of some parameters will not be used, you can use their require_ Grad is set to False. For example, if we want to use a pre-trained CNN, we will fix all the convolution pooling layer parameters before the last full connection layer, coded as follows:

import torch.nn as nn
import torchvision
model = torchvision.models.resnet18(pretrained=True)
for param in model.parameters():
  param.requires_grad = False
 
# Replace the last full connection layer with the newly constructed one
# By default, requires_of newly constructed modules Grad=True
model.fc = nn.Linear(512, 100)

# The optimizer adjusts only the parameters of the newly constructed fully connected layer.
optimizer = torch.optim.SGD(model.fc.parameters(), lr=1e-2, momentum=0.9)

Volatile is available after 0.4.0 and deprecated, but we'll use previous versions for later code, so you need to know about it. It works well in scenarios where there is no need to call the backward() function at all. It's more than requires_grad is more efficient, and if volatile is True, it forces require_ Grade is also True. It and requires_ The difference between grad is that if requires_of all inputs to an operation When grad is all False, requires_of this Operation Grad is False, and this Operation does not participate in the calculation of gradients; If one of the inputs to an Operation is that volatile is True, then that Operation's volatile is True, then the Operation will not participate in the calculation of the gradient. It is therefore appropriate for predicting scenarios where, instead of modifying any definition of the model, only setting the input variable (one) to volatile, no intermediate results for backward are retained in the forward calculation, which greatly improves the speed of prediction.