I have the idea of using python to solve Sudoku in my spare time, but because I still don't know anything about the more complicated algorithms, I finally realized it with simple algorithms.

Relevant Introduction:

1. The algorithm used is very conventional and well understood, which is somewhat similar to the depth-first search algorithm.
2. It takes about 50-150 MS to solve the routine difficulty of Sudoku, but the super-difficult Sudoku on the Internet can not be solved in a short time. --0
3. Inputting Sudoku data requires either inputting a row of players or replacing default_data data data in the program. In short, there is no graphical interface, so it is a little inconvenient to input Sudoku data.

It may continue to optimize performance, or it may change to a graphical interface.~

Usage method:

Mainly input introduction, I set up two kinds, before the game starts, I can choose "1" or "2":

***Method 1: Modify the default sudoku***
***Method 2: Through input method***

Please select the data input method: 1 or 2

• 1: Direct modification of default_data given in the program, the number of modifications, please fill in the blank 0.
  As shown below (the initial Sudoku of default_data can also run ~):

default_data = [[1 ,0 ,6 ,2 ,0 ,0 ,0 ,0 ,0 ],
                [0 ,0 ,0 ,4 ,0 ,0 ,8 ,2 ,0 ],
                [2 ,0 ,0 ,0 ,0 ,5 ,0 ,0 ,0 ],
                [0 ,8 ,0 ,0 ,4 ,0 ,0 ,0 ,7 ],
                [0 ,0 ,0 ,6 ,0 ,3 ,0 ,0 ,0 ],
                [5 ,0 ,0 ,0 ,1 ,0 ,0 ,4 ,0 ],
                [0 ,0 ,0 ,9 ,0 ,0 ,0 ,0 ,0 ],
                [0 ,3 ,9 ,0 ,0 ,4 ,0 ,0 ,0 ],
                [0 ,0 ,0 ,0 ,0 ,2 ,9 ,0 ,5 ]]

• 2: input() + for loops, enter the code line by line, enter one line to confirm, then press Enter to enter the next line. After all nine lines are input, you can confirm it again and start the calculation again.
  As shown below (the number keys in each row are spaced by spaces):

***Method 1: Modify the default sudoku***
***Method 2: Through input method***

Please select the data input method: 1 or 2
2
Enter 1th line: 1 0 6 2 0 0 0 0 0
Enter 2th line: 0 0 0 4 0 0 8 2 0
Enter 3th line: 2 0 0 0 0 5 0 0 0
Enter 4th line: 0 8 0 0 4 0 0 0 7
Enter 5th line: 0 0 0 6 0 3 0 0 0
Enter 6th line: 5 0 0 0 1 0 0 4 0
Enter 7th line: 0 0 0 9 0 0 0 0 0
Enter 8th line: 0 3 9 0 0 4 0 0 0
Enter 9th line: 0 0 0 0 0 2 9 0 5

When you finish typing, you print the Sudoku you entered, then ask if you confirm it, then you can get the answer by typing Y confirmation, and then re-typing N:

Your data:
 1  0  6  2  0  0  0  0  0 
 0  0  0  4  0  0  8  2  0 
 2  0  0  0  0  5  0  0  0 
 0  8  0  0  4  0  0  0  7 
 0  0  0  6  0  3  0  0  0 
 5  0  0  0  1  0  0  4  0 
 0  0  0  9  0  0  0  0  0 
 0  3  9  0  0  4  0  0  0 
 0  0  0  0  0  2  9  0  5 
Confirm? Y or N

Principle introduction

There are two main functions:

• judge, which is used to determine whether a number is allowed to be filled in at any point in the Sudoku matrix, is relatively simple.

def judge(data, x, y, num): 
    if data[y].count(num) > 0:   #Row judgment
        #print('error1')
        return False

    for col in range(9):   #Column judgement
        if data[col][x] == num:
            #print('error2')
            return False

    for a in range(3):   #Nine Gongge Judgment
        for b in range(3):
            if data[a+3*(y//3)][b+3*(x//3)] == num:
                #print('error3')
                return False
    return True

• fill_num, which fills in the blank with the number allowed by the judge function, then fills in the next blank, and then the next one... (yes, this is an iteration process)... until a certain blank occurs when judge is False, the amount pass will be dropped; until all the blanks are filled and judge is True, the filled data matrix will be returned.
  By the way, we also introduce the build_data_list function, which is used to initialize and create a list of alternative numbers for each vacancy, as follows:

def build_data_list(data):   
    data_list = []
    for y in range(9):
        for x in range(9):
            if data[y][x] == 0:
                data_list.append([(x, y), [1, 2, 3, 4, 5, 6, 7, 8, 9]])   #The list contains coordinate information and alternative numbers
    return data_list

An alternative list is created for each empty place, and the fill_num function iterates over all empty places and loops through the alternative list. Alternate lists can be screened out before each step to improve speed, but this part of the work has not yet been done.

The fill_num function code is as follows:

def fill_num(data, data_list, start): 
    if start < len(data_list):
        one = data_list[start]
        for num in one[1]:
            if judge(data, one[0][0], one[0][1], num):
                data[one[0][1]][one[0][0]] = num
                tem_data = fill_num(data, data_list, start+1)   #Iteration part
                if tem_data != None:
                    return tem_data   #When the iteration return value is not empty, it is passed to the upper layer
        data[one[0][1]][one[0][0]] = 0   #When for loops ends, you need to perform a zeroing operation
    else:
        return data

There are holes in the fill_num function:

• Every empty loop attempt succeeds and leads down to the next empty place until the last empty place.. This is certainly the best case, in which case the correct data will be returned layer by layer without any problem. The figures are as follows:

  
  
  

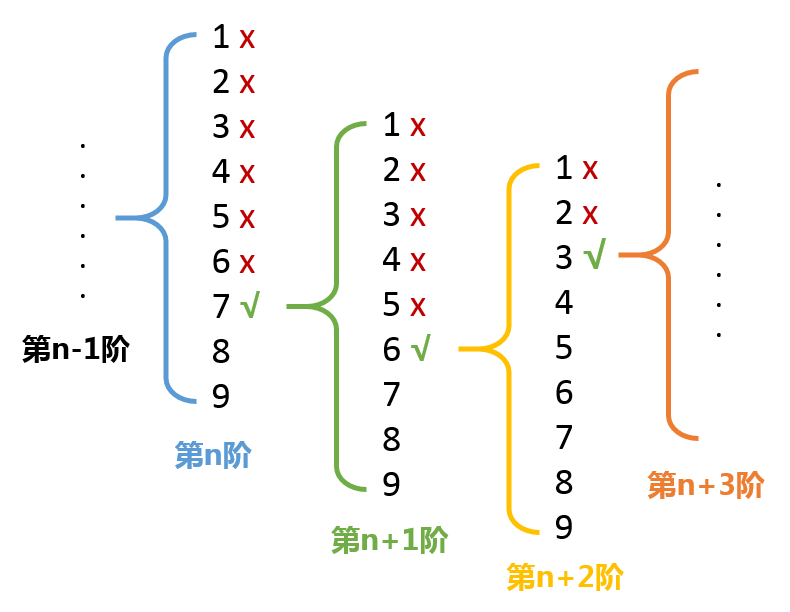  Ideal situation

• But this guessing method of Sudoku is always wrong. This corresponds to the fact that the conjecture of the nth order is judge d to be True, but it is not the answer value, and this kind of mistake often needs to guess many orders down to be reflected. The illustration is as follows, which will form two pits.

  
  
  

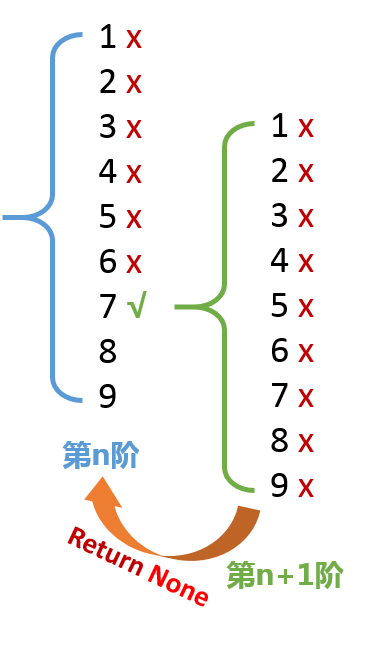  Daily situation

• In pit one, the iteration function of order n+1 also returns a value (except that the value is None) when the number for loops of order n+1 is not found after execution. Once an order function returns a value, its external function returns in turn, and subsequent guesses are terminated, and the correct value is not None.

if tem_data != None:
    return tem_data   #When the iteration return value is not empty, it is passed to the upper layer

Therefore, this part of the code is added to avoid the end of a function for loops, when the return value is None, causing the outer function to return continuously and interrupt the operation.

• Firstly, the problem of return value is solved. Secondly, although the return value is checked and guaranteed, after all, one or more levels of for loops have been executed incorrectly, resulting in data being assigned incorrectly many times:

if judge(data, one[0][0], one[0][1], num):   #Assignment is allowed if judge is True
    data[one[0][1]][one[0][0]] = num

The solution is that once the for loops can be fully executed, it indicates that there must be a mistake in the previous filling, so the number of each mistake should be zero:

data[one[0][1]][one[0][0]] = 0   #When for loops ends, you need to perform a zeroing operation

It's no big problem to solve these two pits.

Here's the file, enjoy yourself~
Sudoku v2

Sudoku v2