Title Description:

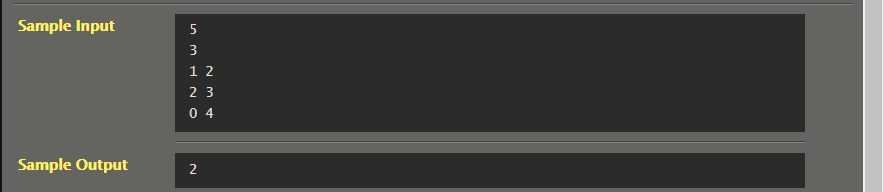
  Resolution:

This problem is abstracted as finding the number of connected subgraphs of a graph. DFS traversal can be used to calculate the connectivity; Or use and query set.

This question uses and looks up the set.

(1) Initialization: initialize the parent node of each node as itself. At this time, n nodes have n circles of friends;

(2) Step 1: according to the input sequence, initialize the node array and the corresponding father array for the second wave. Note that father[tail]=head, so as to successfully stop when looking from back to front;

(3) Step 3: traverse. For each node in the node, find its parent node. If this node is equal to its parent node, that is, father[node]=node, it means that the ancestor node has been found, stop searching this node and jump to the next node. On the contrary, if its ancestor node has not been found, make the parent node of the current node equal to the parent node of its parent node, and then compare and update. After that, the parent node of this node is compared with the parent node of the parent node until it is the same.

(4) Finally, organize it into a dictionary to get the number of circles of friends.

Knowledge points:

(1) enumerate() function

——Syntax: enumerate(sequence, [start=0])

——Parameter: sequence is a sequence, iterator or other iteration object; Start subscript start position;

——Return value: returns the enumerate enumeration object;

>>>seasons = ['Spring', 'Summer', 'Fall', 'Winter']
>>> list(enumerate(seasons))
[(0, 'Spring'), (1, 'Summer'), (2, 'Fall'), (3, 'Winter')]
>>> list(enumerate(seasons, start=1))       # Subscript starts with 1
[(1, 'Spring'), (2, 'Summer'), (3, 'Fall'), (4, 'Winter')]

(2) Joint search set

Understand the idea and basic operation mode of search set: that is, always update a node. The first time is its own parent node, and the second time its parent node becomes the parent node of its parent node, that is, the master node. Then compare whether its parent node (that is, the master node) is the same as the master node (that is, the master node). If it is the same, break stops looking for the node. If it is different, update its parent node as the master node. And always.

The core code is as follows:

for node in nodes:
    while True:
        # For each node, find its parent node and see who the parent node of its parent node is until it is found that the parent node is the same as the node, which means the end
        father_of_node=father[node]
        if father_of_node!=father[father_of_node]:
            father[node]=father[father_of_node]
        else:
            break

code:

n=int(input())
nodes=list(range(n))
father=list(range(n))

m=int(input())
edges=[]
for i in range(m):
    edge=[int(i) for i in input().split(' ')]
    edges.append(edge)
for edge in edges:
    head=edge[0]
    tail=edge[1]
    father[tail]=head
for node in nodes:
    while True:
        # For each node, find its parent node and see who the parent node of its parent node is until it is found that the parent node is the same as the node, which means the end
        father_of_node=father[node]
        if father_of_node!=father[father_of_node]:
            father[node]=father[father_of_node]
        else:
            break
dic={}
for i,f in enumerate(father):
    dic[f]=[]
print(len(dic))

Extended knowledge:

This problem can also be obtained by DFS traversal.

(1) Principle: after DFS is performed on each node, all nodes connected to it will be found and marked. Therefore, the number of connected subgraphs depends on how many times DFS is executed;

(2) Implementation method: at the beginning, each node didn't walk through. For each node, judge whether it has passed, that is, used[i]==1. If not, DFS will be implemented. At the same time, k + +, mark that DFS has been implemented several times. For each DFS, it finds all nodes connected to it by constantly calling itself.

The basic code is as follows:

n=int(input())
dis=[[0 for i in range(n)]for j in range(n)]
used=[0 for i in range(n)]
m=int(input())
for i in range(m):
    a=[int(i) for i in input().split(' ')]
    dis[a[0]][a[1]]=1
    dis[a[1]][a[0]]=1

def DFS(i,n):
    used[i]=1
    for j in range(n):
        if dis[i][j]==1:
            if used[j]!=1:
                DFS(j,n)
k=0
for i in range(n):
    if used[i]==0:
        k+=1
        DFS(i,n)
print(k)