1. Tuples

What is tuple

• Tuple: One of Python's built-in data structures is an immutable sequence
  • Example:

t = ( 'python' , 'hello' , 90 )

• Variable and Invariant Sequences
  • Invariant sequence: string, tuple
    • No add, delete, change operations for immutable sequences
  • Variable sequence: list, bullet, set
    • Variable sequences can add, delete, and change sequences without changing object addresses
• Why python designed tuples as immutable sequences
  • In a multitask environment, there is no need to lock objects simultaneously; therefore, use immutable sequences whenever possible in your program
  • Note: Tuples store references to objects
    • If an object in a tuple is itself an immutable object, you cannot reference other objects
    • If the object in the tuple is a mutable object, the reference to the mutable object is not allowed to change, but the data can change
    • Diagrams and codes:
      

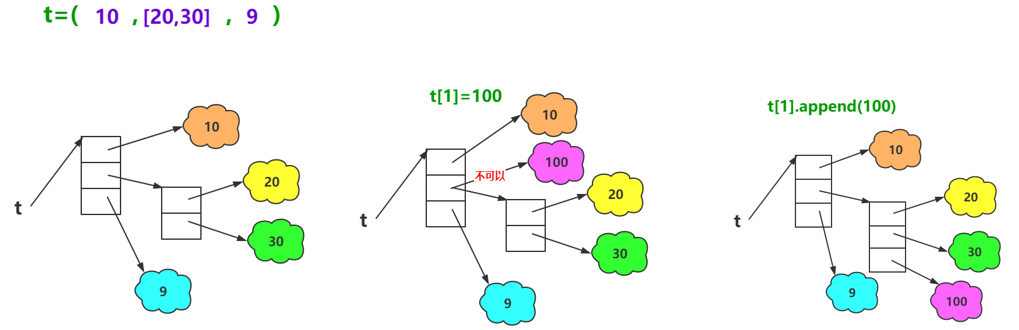
t = (10, [20, 30], 9)
print(t[1], type(t[1]), id(t[1]))  # [20, 30] <class 'list'> 2275937298112

"""Try to t[1]Change to 100"""
# t[1]=100 #Tuples do not allow modification of elements
"""Because t[1]=[20,30]List,
A list is a variable sequence.
So you can add elements to the list,
The memory address of the list does not change"""
t[1].append(100)  # Add an element to the list
print(t[1], id(t[1]))  # [20, 30, 100] 2275937298112

How tuples are created

• Use parentheses, which can be omitted

t = ( 'python' , 'hello' , 90 )
t2='python','world',98		#Omit parentheses

• Using the built-in function tuple()

t1=tuple(('python','wof'))

• Tuples containing only one element need to be commas plus parentheses

t3=('python',)

Traversal of tuples

• Tuples are iterative objects, so you can traverse them using for-in

t=('python','world',98)
for item in t:
    print(item)

2. Sets

What is a collection

• One of python's built-in data structures
• Like lists and dictionaries, mathematical variable sequences
• A collection is a dictionary without a Value
• Elements in a collection are out of order and do not allow duplication

How collections are created

• Create directly, using {}
• Using the built-in function set()
• Where defining an empty collection can only be set()

s6 = {}  # dict dictionary type
print(type(s6))  # <class 'dict'>

s7 = set()
print(type(s7))  # <class 'set'>

Add, delete, check, change and so on to a collection

• Judgement of Collection Elements
  • In and not in
• Addition of Collection Elements
  • Call the add() method: add one element at a time
  • Call the updata() method: add at least one element at a time
• Delete operation of collection
  • Call the remove() method: only one element can be deleted at a time, and a KeyError exception is thrown if the specified element does not exist
  • Call discard() method: Delete one specified element at a time, and do not throw an exception if the calling element does not exist
  • Call the pop() method: delete one arbitrary element at a time, the method is parameterless
  • Call the clear() method: empty all elements in the collection

Relation 1 Before Set

• Is two sets equal
  • You can use the operator==or!=Make a judgment
• Is one set a subset of another
  • The method issubset can be called for judgment
• Is one set a superset of another
  • The method issuperset can be called for judgment
• Does Two Sets Intersect--Has Intersection Is False
  • The method isdisjoin can be called for judgment

'''Whether two sets are equal (elements are the same, they are the same)'''
s = {10, 20, 30, 40}
s2 = {30, 40, 20, 10}
print(s == s2)  # The elements in the True collection are out of order
print(s != s2)  # False

"""Is one set a subset of another"""
s1 = {10, 20, 30, 40, 50, 60}
s2 = {10, 20, 30, 40}
s3 = {10, 20, 90}
print(s2.issubset(s1))  # True
print(s3.issubset(s2))  # False

'''Is one set a superset of another'''
print(s1.issuperset(s2))  # True
print(s2.issuperset(s1))  # False

'''Whether two sets contain intersections'''
print(s1.isdisjoint(s2))  # False with intersection
print(s2.isdisjoint(s3))  # False with intersection 

Relationships between sets 2

• Sketch Map:
  

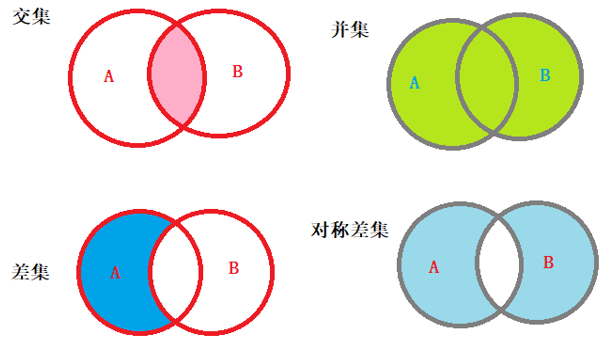
# Mathematical operation of sets
s1 = {10, 20, 30, 40}
s2 = {20, 30, 40, 50, 60}
# 1. Intersection operation, original set does not change
print(s1.intersection(s2))  # {40, 20, 30}
print(s1 & s2)  # intersection() equivalent &

# 2. Union operation, original set does not change
print(s1.union(s2))  # {40, 10, 50, 20, 60, 30}
print(s1 | s2)  # union() is equivalent to |

# 3. Differential set operation, original set does not change
print(s1.difference(s2))  # {10}, take the part not found in s2 in s1
print(s1 - s2)

# 4. Symmetric difference set, original set does not change
print(s1.symmetric_difference(s2))  # {50, 10, 60}, take the non-repeating parts from s1 and s2
print(s1 ^ s2)

Generative Forms of Sets

• Formulas used to generate sets

  { i*i for i in range(1,10) }
  

  • Modifying {} to [] is list generation
  • No tuple generation

  # List Generation
  lst = [i * i for i in range(6)]
  print(lst)  # [0, 1, 4, 9, 16, 25]
  
  # Collection Generation
  lst1 = {i * i for i in range(6)}
  print(lst1)  # {0, 1, 4, 9, 16, 25}
  

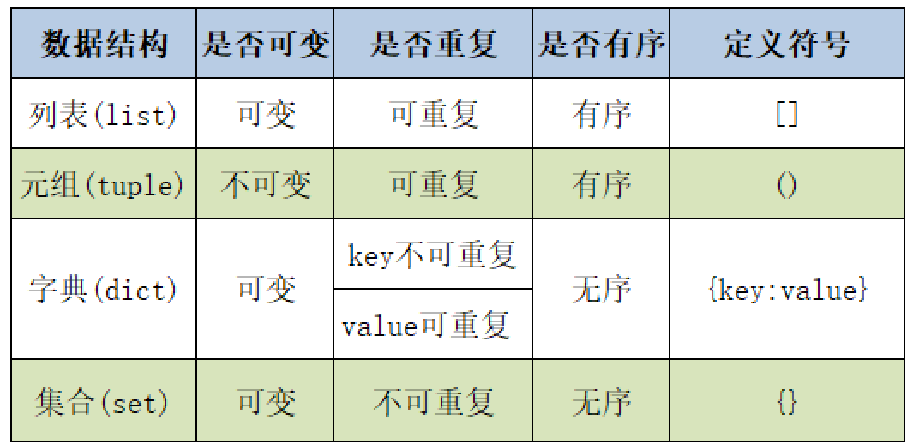
3. Summary of lists, dictionaries, tuples and collections