Please like it when it's useful, and comment when it's useless.

Welcome to share this article, reprint please keep the source.

The principle of logistic expression model can refer to these two Blogs:

https://www.jianshu.com/p/4cf34bf158a1

https://blog.csdn.net/c406495762/article/details/77723333

The formula used by these two blogs in training the model is:

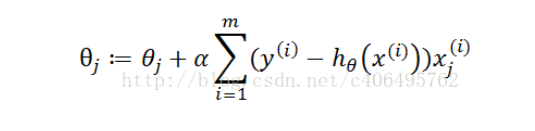
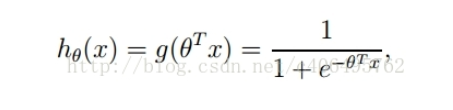
, that is to say, implementation method 2 in the code. In addition, according to the log likelihood function above the statistical learning method of Li Hang, I have deduced the gradient formula as follows:

The adopted data set is MNIST data set with only two types of label(0,1):

# -*- coding:utf-8 -*-
# Logistic expression, logistic regression, MLE model. Refer to Li Hang's statistical learning method for algorithm
#author:Tomator

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split


class Logistic_regression(object):
    def __init__(self,learn_rate,max_interation):
        self.learn_rate=learn_rate
        self.max_interation=max_interation
        self.w=None

    # For the first method, refer to Li Hang's statistical learning method
    def train(self,train_vector,train_label):
        train_nums,train_feture_nums=train_vector.shape
        print("train_data",train_nums,train_feture_nums)
        train_label=train_label.reshape(train_nums,1)
        train_label = np.tile(train_label, (1, train_feture_nums))
        self.w=np.zeros(train_feture_nums)
        interations=1
        # while interations < self.max_interation:
        while interations < self.max_interation:
            alpha_y=np.exp(np.dot(self.w,train_vector.T)) / (1 + np.exp(np.dot(self.w,train_vector.T)))
            alpha_y=alpha_y.reshape((train_nums,1))
            alpha_y=np.tile(alpha_y,(1,train_feture_nums))
            # print(alpha_y.shape,train_label.shape)
            alpha_w=np.sum(train_label*train_vector-train_vector*alpha_y)
            self.w=self.w+alpha_w
            # print(self.w.shape)
            interations+=1

        self.w=self.w.reshape((1,train_feture_nums))
        return self.w

    def predict(self, vector):
        # vector=vector.reshape((784,1))
        exp_wx=np.exp(np.dot(self.w,vector.T))
        predict_1=exp_wx/(1+exp_wx)
        predict_2=1/(1+exp_wx)
        # print("predict",predict_1,predict_2)
        if predict_1 > predict_2:
            return 0
        else:
            return 1

    # The second implementation method
    def sigmoid(self,z):
        return 1.0 / (1 + np.exp(-z))

    def train2(self, train_vector, train_label):
        train_nums, train_feture_nums = train_vector.shape
        print("train_data", train_nums, train_feture_nums)
        self.w = np.zeros(train_feture_nums)
        print(self.w.shape)
        interations = 1
        while interations < self.max_interation:
            v = np.dot(self.w, train_vector.T)
            error = train_label - self.sigmoid(v)
            # print(train_label.shape,error.shape)
            self.w += self.learn_rate * np.dot(error, train_vector)
            # print(self.w.shape)
            interations += 1
        return self.w

    def predict2(self, x):
        PT = self.sigmoid(np.dot(self.w,x.T))
        if PT > 1 - PT:
            return 1
        else:
            return 0


if __name__ == "__main__":

    np.seterr(divide='ignore', invalid='ignore')
    """
    //When pandas's read_csv() method is called, C engine is used as the parser engine by default. When the file name contains Chinese, C engine will make mistakes in some cases. So when you call the read_csv() method, you can specify engine as Python to solve the problem.
    """
    data=pd.read_csv("D:\\python3_anaconda3\\Study\\machine learning\\Machine learning data set\\MNIST Data sets - two types label\\train_binary.csv",skiprows=1,engine='python')
    data = data.values[1:,:]
    data=np.array(data)

    # Divide training set and test set
    train_data,test_data = train_test_split(data,test_size=0.3, random_state=0)
    # The first line of CSV file is header, which should be removed when converting to numpy array
    train_vector=train_data[:,1:]
    train_label=train_data[:,0]
    test_vector=test_data[:,1:]
    test_label=test_data[:,0]

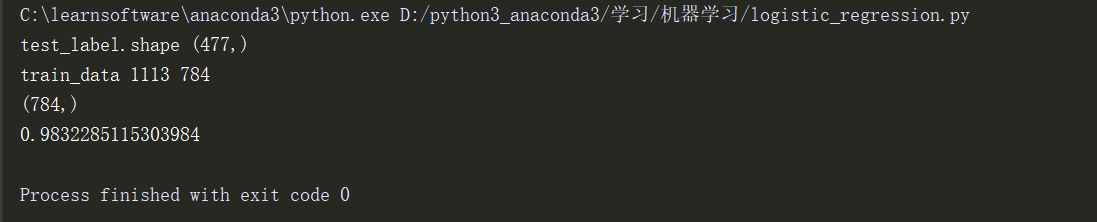
    print("test_label.shape",test_label.shape)
    logistic=Logistic_regression(learn_rate=0.00001,max_interation=5000)
    logistic.train(train_vector,train_label)

    score=0
    for vector,label in zip(test_vector,test_label):
        if logistic.predict(vector) == label:
            score+=1
    print(score/len(test_label))

The output of the first method is slow in training time.

The output of the second method is faster.