Hierarchical Clustering
I. Concepts
Hierarchical clustering does not require specifying the number of clusters. First, it considers each instance in the data as a class, then merges the two most similar classes. This process iterates until only one class is left, and the classes are made up of two subclasses, each of which is made up of two smaller subclasses.As shown in the following figure:

2. Consolidation Method
In a cluster, two nearest classes are merged for each iteration, and there are three common methods for calculating the distance between these classes:
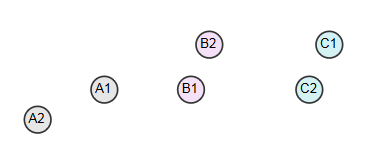
1. Single-link clustering
In a single-join cluster, the distance between two classes is defined as the shortest distance between all instances of one class and all instances of another class.As in the figure above, the shortest distance between Classes A(A1,A2), B(B1,B2), C(C1,C2), A and B is A1 to B1, so Class A is closer to Class B, and all A and B merge.
2. Complete-link clustering
In a fully connected cluster, the distance between two classes is defined as the longest distance between all instances of one class and all instances of another class.The longest distance between classes A and B is A2 to B2, and the longest distance between classes B and C is B1 to C1, distance (B1-C1) < distance (A2-B2), so classes B and C are merged.
3. Average-link clustering
In average join clustering, the distance between classes is the average distance from all instances of one class to all instances of another class.
3. python implementation (single connection)
1 #!/usr/bin/python 2 # -*- coding: utf-8 -*- 3 4 from queue import PriorityQueue 5 import math 6 import codecs 7 8 9 """ 10 hierarchical clustering 11 """ 12 class HCluster: 13 14 #Median of a column 15 def getMedian(self,alist): 16 tmp = list(alist) 17 tmp.sort() 18 alen = len(tmp) 19 if alen % 2 == 1: 20 return tmp[alen // 2] 21 else: 22 return (tmp[alen // 2] + tmp[(alen // 2) - 1]) / 2 23 24 #Normalize numeric data using absolute standard score[Absolute standard deviation->asd=sum(x-u)/len(x),x Standard score->(x-u)/Absolute standard deviation, u Median] 25 def normalize(self,column): 26 median = self.getMedian(column) 27 asd = sum([abs(x - median) for x in column]) / len(column) 28 result = [(x - median) / asd for x in column] 29 return result 30 31 def __init__(self,filepath): 32 self.data={} 33 self.counter=0 34 self.queue=PriorityQueue() 35 line_1=True#First line at beginning 36 with codecs.open(filepath,'r','utf-8') as f: 37 for line in f: 38 #First Behavior Description Information 39 if line_1: 40 line_1=False 41 header=line.split(',') 42 self.cols=len(header) 43 self.data=[[] for i in range(self.cols)] 44 else: 45 instances=line.split(',') 46 toggle=0 47 for instance in range(self.cols): 48 if toggle==0: 49 self.data[instance].append(instances[instance]) 50 toggle=1 51 else: 52 self.data[instance].append(float(instances[instance])) 53 #Normalized numeric column 54 for i in range(1,self.cols): 55 self.data[i]=self.normalize(self.data[i]) 56 57 #Euclidean distance calculation elements i Distance to all other elements, in the neighborhood dictionary, for example i=1,j=2...,Structures such as i=1 Neighbors->{2: ((1,2), 1.23), 3: ((1, 3), 2.3)... } 58 #Find Nearest Neighbor 59 #Put elements in priority queue based on nearest neighbors 60 #data[0]Place label Label, data[1]and data[2]Is a numeric property 61 rows=len(self.data[0]) 62 for i in range(rows): 63 minDistance=10000 64 nearestNeighbor=0 65 neighbors={} 66 for j in range(rows): 67 if i!=j: 68 dist=self.distance(i,j) 69 if i<j: 70 pair=(i,j) 71 else: 72 pair=(j,i) 73 neighbors[j]=(pair,dist) 74 if dist<minDistance: 75 minDistance=dist 76 nearestNeighbor=j 77 #Create Nearest Neighbor Pair 78 if i<nearestNeighbor: 79 nearestPair=(i,nearestNeighbor) 80 else: 81 nearestPair=(nearestNeighbor,i) 82 #Put in the priority column,(Nearest Neighbor Distance, counter,[label Tag name, nearest neighbor tuple, all neighbors]) 83 self.queue.put((minDistance,self.counter,[[self.data[0][i]],nearestPair,neighbors])) 84 self.counter+=1 85 86 #Euclidean distance,d(x,y)=math.sqrt(sum((x-y)*(x-y))) 87 def distance(self,i,j): 88 sumSquares=0 89 for k in range(1,self.cols): 90 sumSquares+=(self.data[k][i]-self.data[k][j])**2 91 return math.sqrt(sumSquares) 92 93 #clustering 94 def cluster(self): 95 done=False 96 while not done: 97 topOne=self.queue.get() 98 nearestPair=topOne[2][1] 99 if not self.queue.empty(): 100 nextOne=self.queue.get() 101 nearPair=nextOne[2][1] 102 tmp=[] 103 #nextOne Is it topOne Nearest neighbor, if not continued 104 while nearPair!=nearestPair: 105 tmp.append((nextOne[0],self.counter,nextOne[2])) 106 self.counter+=1 107 nextOne=self.queue.get() 108 nearPair=nextOne[2][1] 109 #Add back Pop Output unequal nearest neighbor elements 110 for item in tmp: 111 self.queue.put(item) 112 113 if len(topOne[2][0])==1: 114 item1=topOne[2][0][0] 115 else: 116 item1=topOne[2][0] 117 if len(nextOne[2][0])==1: 118 item2=nextOne[2][0][0] 119 else: 120 item2=nextOne[2][0] 121 #Join two nearest neighbors to form a new family 122 curCluster=(item1,item2) 123 #Neighbor distance elements in the new family are established using the single-join method below. First, the nearest neighbors of the new family above are calculated.2. Create new neighbors.If item1 and item3 The distance is 2, item2 and item3 Distance is 4, then the distance in the new family is 2 124 minDistance=10000 125 nearestPair=() 126 nearestNeighbor='' 127 merged={} 128 nNeighbors=nextOne[2][2] 129 for key,value in topOne[2][2].items(): 130 if key in nNeighbors: 131 if nNeighbors[key][1]<value[1]: 132 dist=nNeighbors[key] 133 else: 134 dist=value 135 if dist[1]<minDistance: 136 minDistance=dist[1] 137 nearestPair=dist[0] 138 nearestNeighbor=key 139 merged[key]=dist 140 if merged=={}: 141 return curCluster 142 else: 143 self.queue.put((minDistance,self.counter,[curCluster,nearestPair,merged])) 144 self.counter+=1 145 146 if __name__=='__main__': 147 hcluser=HCluster('filePath') 148 cluser=hcluser.cluster() 149 print(cluser)
Reference: 1.machine.learning.an.algorithmic.perspective.2nd.edition.
2.a programmer's guide to data mining