preface

This is a work of my junior last semester. Then, in order to display the intermediate process, it is written with the idea of process oriented.

• Note: it is strongly recommended to run code with jupyter
• n stands for running sequence
  • In [n]: represents step n
  • Out [n]: represents the input corresponding to the operation in step n
  • In []: for not running

get ready

Unified data structure (take 65535 as an example)

In [1]:

import numpy as np

32-bit binary (list form)

In [2]:

# Example: array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], dtype=np.uint8)

# Decimal to 32-bit binary
def Dec_to_Bin(Dec):
    Dec %= 2**32
    return np.array([Dec >> tmp & 1 for tmp in range(32)][::-1], dtype = np.uint8)

# Hex to 32-bit binary
def Hex_to_Bin(Hex):
    return Dec_to_Bin(eval('0x' + Hex))

decimal system

In [3]:

# Example: 65535

# Binary to decimal
def Bin_to_Dec(Bin):
    Dec = 0
    for i in range(len(Bin)):
        Dec += Bin[-i-1] * 2 ** i
    return Dec

# Hex to decimal
def Hex_to_Dec(Hex):
    return eval('0x' + Hex)

8-bit hex (string form)

In [4]:

# Example: '0000ffff'

# 32-bit binary to 8-bit hexadecimal
def Bin_to_Hex(Bin):
    Hex = ''
    for i in range(len(Bin)//4):
        tmp = hex(Bin_to_Dec(Bin[4 * i : 4 * (i + 1)]))[-1]
        Hex += str(tmp)
    return Hex

# Decimal to 8-digit hexadecimal
def Dec_to_Hex(Dec):
    Dec %= 2**32
    Hex = ''
    for tmp1 in [hex(Dec >> (tmp2 * 4) & 0xf)[-1] for tmp2 in range(8)][::-1]:
        Hex += str(tmp1)
    return Hex

64 bit hex (string form)

In [5]:

# Decimal to 64 bit hex
def Dec_to_Hex_64(Dec):
    Hex = ''
    for tmp1 in [hex((Dec) >> (tmp2 * 4) & 0xf)[-1] for tmp2 in range(64)][::-1]:
        Hex += str(tmp1)
    return Hex

Define cyclic left shift and bitwise inverse functions

In [6]:

# Cycle shift left
def cycle_left(X, n, dtype):
    if dtype == 'Bin':
        n = n % 32
        return Bin_to_Dec(np.append(X[n:], X[:n]))
    elif dtype == 'Dec':
        return cycle_left(Dec_to_Bin(X), n, 'Bin')
    elif dtype == 'Hex':
        return cycle_left(Hex_to_Bin(X), n, 'Bin')
    else:
        raise TypeError("Binary, please enter np_bin and Bin，Decimal, please enter num and Dec，Hex, please enter str and Hex")

In [7]:

# Bitwise inversion
def invert(X, dtype):
    if dtype == 'Bin':
        for i in range(len(X)):
            if X[i] == 0:
                X[i] = 1
            else:
                X[i] = 0
        return Bin_to_Dec(X)
    elif dtype == 'Dec':
        return invert(Dec_to_Bin(X), 'Bin')
    elif dtype == 'Hex':
        return invert(Hex_to_Bin(X), 'Bin')
    else:
        raise TypeError("Binary, please enter np_bin and Bin，Decimal, please enter num and Dec，Hex, please enter str and Hex")

One way hash function SHA-1

In [8]:

%%html
<img src='sha1.png', width=700>

Out [8]:

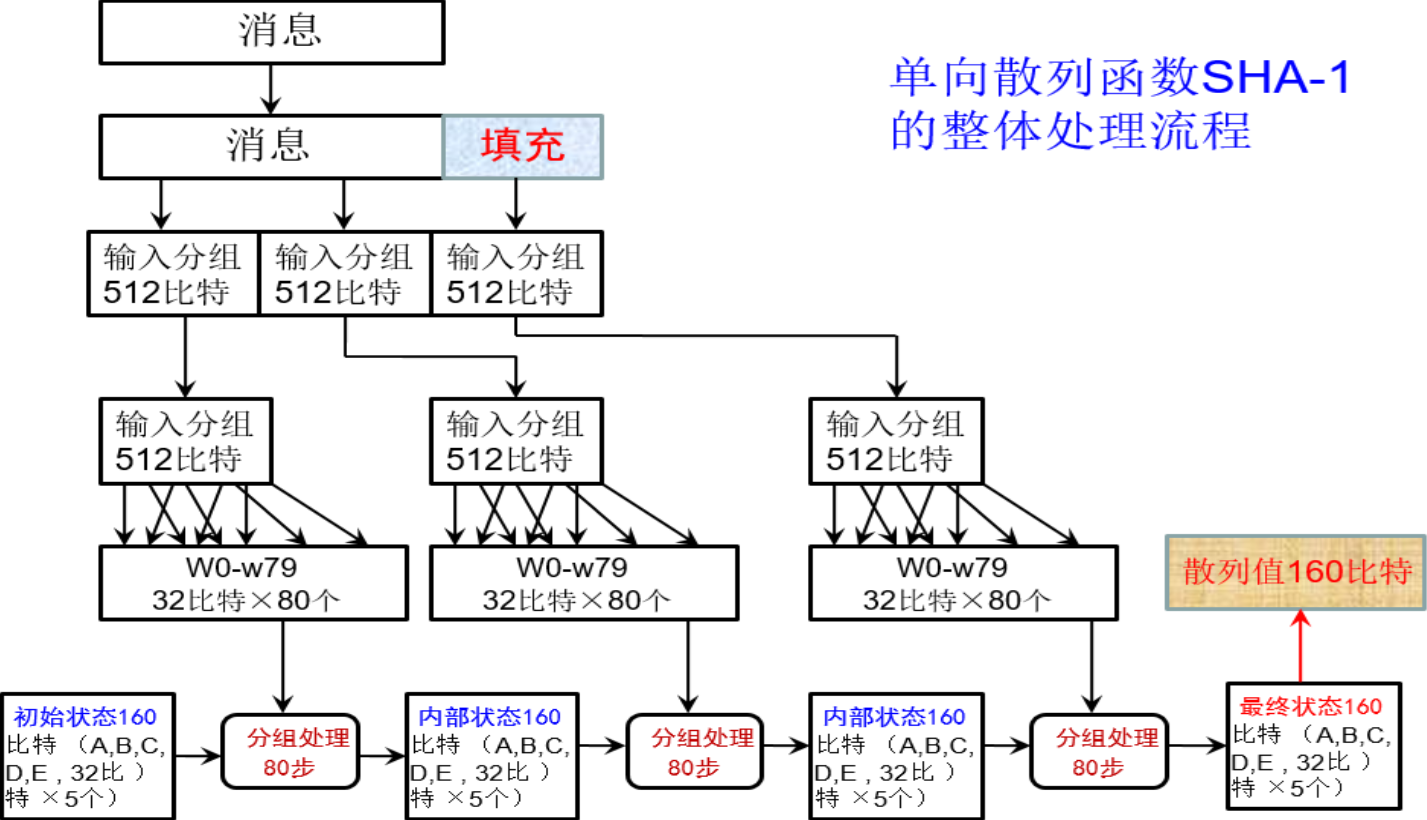
Step 1: fill

The message is populated so that its length is an integer multiple of 512 bits. 512 bits as a packet.
In [9]:

# Message m
m = b'Hello.' * 1

In [10]:

# Message - > ASCII - > binary
ASCII = np.frombuffer(m, dtype = np.uint8)
Bit = np.unpackbits(ASCII)

In [11]:

# Assume that the length of message m is l bits
l = len(Bit)
print("The original message length is %d Bit" % l)

Out [11]:

The original message length is 48 bits

In [12]:

# Add a 1-bit value "1", N, at the end of the message_ 512_ Bit represents 512 integer multiple bits
ONE = np.ones(1, dtype = np.uint8)
N_512_Bit = np.append(Bit, ONE)

In [13]:

# N is a multiple of 512 bit length
# K is the number of 0 to be added, satisfying l + 1 + k = 448mod512
N = 1
while True:
    if l + 1 + 64 <= 512 * N:
        k = 512 * N - l - 1 - 64
        break
    N += 1

In [14]:

# Add message length (excluding the last packet)
print("Need to add %d individual'0'" % k)
ZEROS = np.zeros(k, dtype = np.uint8)
N_512_Bit = np.append(N_512_Bit, ZEROS)

Out [14]:

399 need to be added'0'

In [15]:

# Save the length of the original message to the last 64 bits of the last packet
last_64_bit = [l >> d & 1 for d in range(64)][::-1]
last_64_bit = np.array(last_64_bit, dtype = np.uint8)
N_512_Bit = np.append(N_512_Bit, last_64_bit)

In [16]:

# Display of filled results (binary representation)
for i in range(len(N_512_Bit)):
    print(N_512_Bit[i], end = '')
    if (i + 1) % 64 == 0:
        print()
    elif (i + 1) % 8 == 0:
        print(end = ' ')
    else:
        pass

Out [16]:

01001000 01100101 01101100 01101100 01101111 00101110 10000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00110000

Calculate W0 ~ W79 for each group

According to the 512 bits of the input packet, 80 32-bit values (W0 ~ W79) are calculated
In [17]:

def message_extension(_512_bit):
    
    # Storage W0 ~ W79
    W = {}
    
    for i in range(80):
        # The 512 bits of the input packet are divided into 32 bits × 16 groups and named W0-W15
        if i < 16:
            W["W" + str(i)] = Bin_to_Dec(_512_bit[32*i:32*(i+1)])
        
        # Calculate the remaining W16-W79
        else:
            W_i_16 = W["W" + str(i - 16)]
            W_i_14 = W["W" + str(i - 14)]
            W_i_8  = W["W" + str(i - 8)]
            W_i_3  = W["W" + str(i - 3)]
            result = W_i_16 ^ W_i_14 ^ W_i_8 ^ W_i_3
            
            # Cyclic shift left 1 bit
            W["W" + str(i)] = cycle_left(result, 1, 'Dec')

    return W

Packet processing

Each input packet is processed in 80 steps in turn: after mixing the values in the 5 buffers with the information of the input packet, 80 steps are processed
After calculating W0-W79, the input packet is also processed in 80 steps as shown in the figure on the next page, which aims to change the internal state according to the information of the input packet. This is done for all input groups.
The internal state of 160 bits is represented by five 32-bit buffers named a, B, C, D and E. These buffers are different concepts from W0-W79. This step is to mix the values of the five buffers with the information of the input packet, and then perform the processing of 80 steps.
The operation completed by these 80 steps is to mix the 512 bit data of the input packet with the 160 bit internal state (5 buffers) maintained by SHA-1. Through the repeated execution of the above 80 steps, SHA-1 can mix all the filled messages into the 160 bit internal state, and the hash value output by SHA-1 is the final internal state (160 bits) after all processing.
In [18]:

%%html
<img src='sha1_3.png', width=700>

Out [18]:

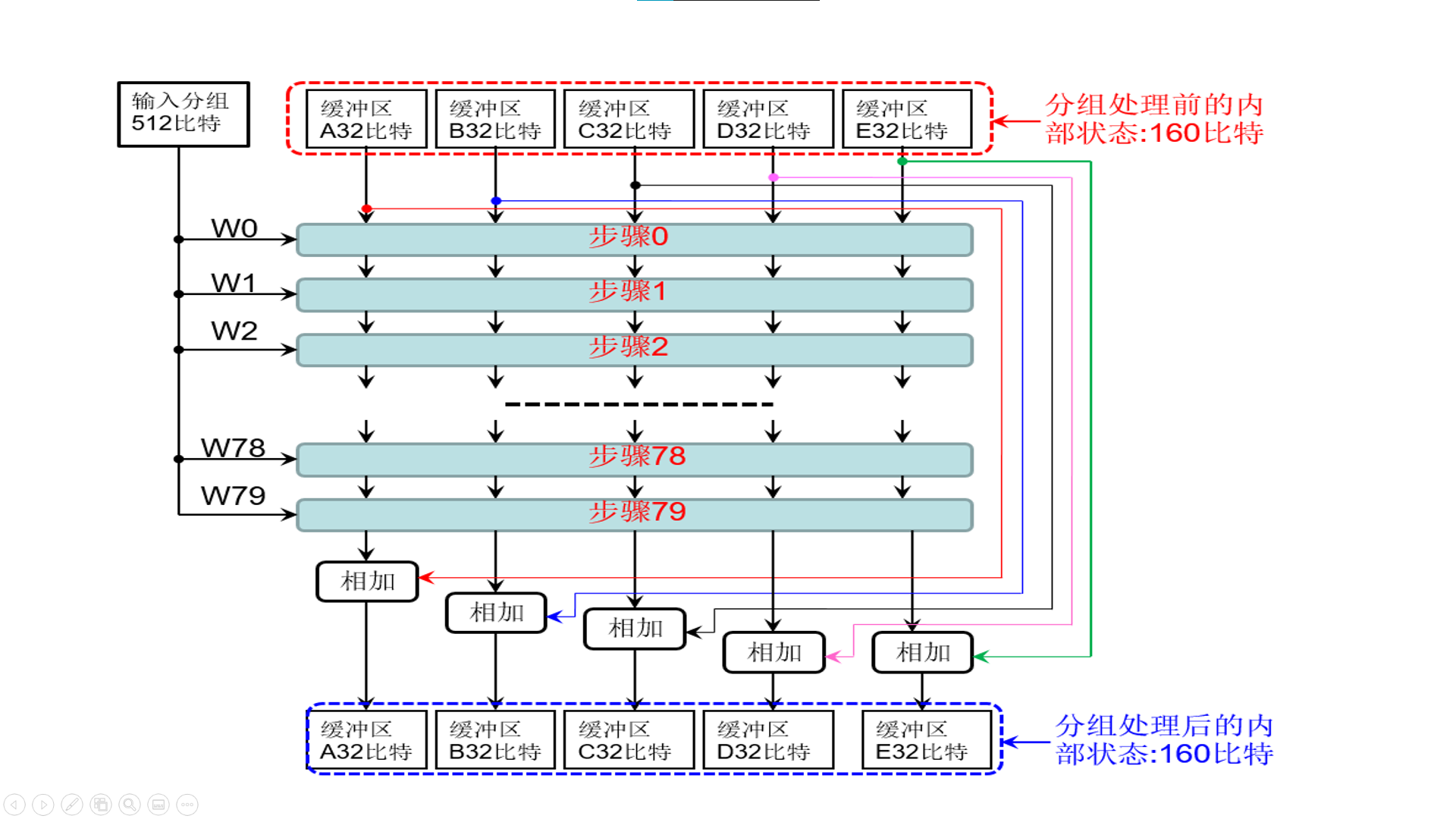
In [19]:

# Grouping by 512 bits
def split_group(N_512_Bit, N):
    print("yes %d Groups" % N)
    Group = {}
    for i in range(N):
        Group["Group" + str(i)] = message_extension(N_512_Bit[512 * i : 512 * (i + 1)])
    return Group

In [20]:

# The filled message M 'is grouped by 512 bits (m_ is used instead of M' in the program)
Group = split_group(N_512_Bit, N)

Out [20]:

There is 1 group

Single step processing

The grouping process is composed of 80 steps, each of which is a process of complex changes in the internal state based on W0-W79
After completing A step, the contents of buffers A, B, C and D will be copied to B, C, D and E respectively (where B will be copied after moving 30 bits to the left), while the contents of buffer partition E will be added with the contents of other buffers and Wt and Kt, and then copied to buffer A
In [21]:

%%html
<img src='sha1_4.png', width=700>

Out [21]:

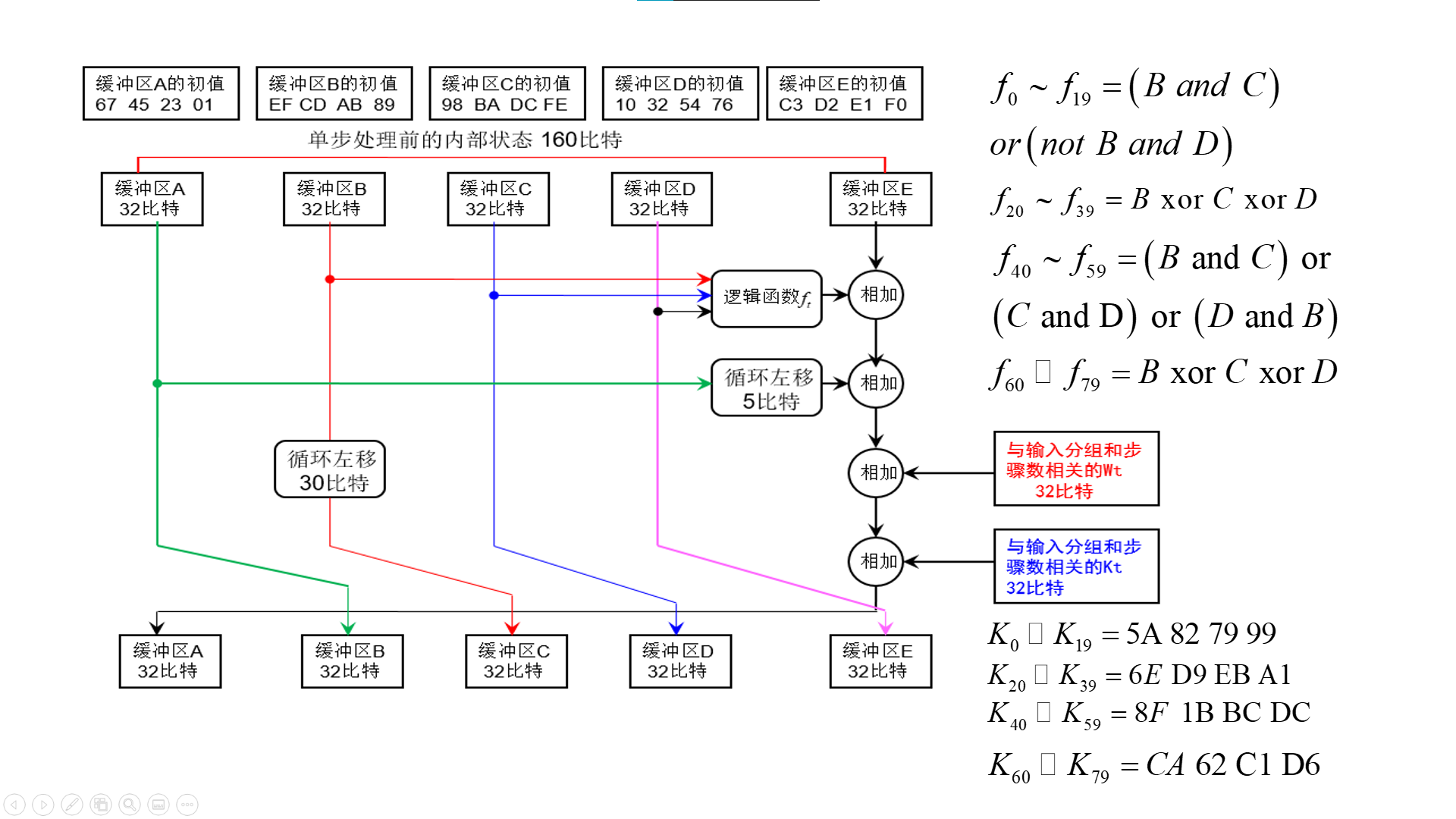
In [22]:

A = 0x67452301
B = 0xEFCDAB89
C = 0x98BADCFE
D = 0x10325476
E = 0xC3D2E1F0

In [23]:

for j in range(len(Group)):
    
    A_ori = A
    B_ori = B
    C_ori = C
    D_ori = D
    E_ori = E
    
    for i in range(80):
        
        if i < 20:
            f = (B & C) | (invert(B, 'Dec') & D)
            K = 0x5A827999
        elif 20 <= i < 40:
            f = B ^ C ^ D
            K = 0x6ED9EBA1
        elif 40 <= i < 60:
            f = (B & C) | (C & D) | (D & B)
            K = 0x8F1BBCDC
        elif 60 <= i < 80:
            f = B ^ C ^ D
            K = 0xCA62C1D6
        
        W = Group['Group' + str(j)]['W' + str(i)]
        
        tmp = D
        D = C
        C = cycle_left(B, 30, "Dec")
        B = A
        A = E + f + cycle_left(A, 5, "Dec") + W + K
        E = tmp
        
    A = A + A_ori
    B = B + B_ori
    C = C + C_ori
    D = D + D_ori
    E = E + E_ori

result

In [24]:

def Binary_to_Hexadecimal(np_bin):
    SHA1 = ''
    for i in range(len(sha1)//4):
        H = hex(Bin_to_Dec(sha1[4 * i : 4 * (i + 1)]))[-1]
        SHA1 += str(H)
    return SHA1

sha1 = np.array([], dtype = np.uint8)
for each in [A, B, C, D, E]:
    sha1 = np.append(sha1, Dec_to_Bin(each))
SHA1 = Bin_to_Hex(sha1)

verification

In [25]:

import hashlib
sha1 = hashlib.sha1(b'Hello.').hexdigest()

In [26]:

print(SHA1)
print(sha1)
SHA1 == sha1

Out [26]:

9b56d519ccd9e1e5b2a725e186184cdc68de0731
9b56d519ccd9e1e5b2a725e186184cdc68de0731
True