1. Processing data

# filename: File path trainingSet: Training set testSet: It is a common practice that the ratio of training data volume to testing data volume is 67/33.
def loadDataset(filename,split,trainingSet=[], testSet=[]):
    with open(filename,'r') as csvfile: #Open a file using the open method
        lines = csv.reader(csvfile) #Using csv module to read data
        dataset = list(lines)
        for x in range(len(dataset)-1):
            for y in range(4):
                dataset[x][y] = float(dataset[x][y])
            if random.random() < split:
            #random.random() is used to generate a random number of 0 to 1: 0 <= n < 1.0.
            #Random segmentation of training data sets and test data sets. It is a common practice that the ratio of training data set to test data set is 67/33, so split is usually 0.66.
                trainingSet.append(dataset[x])
            else:
                testSet.append(dataset[x])

Test code

trainingSet=[]
testSet=[]
loadDataset('iris.data',0.66,trainingSet,testSet)
print('trainingSet',repr(len(trainingSet)))
print('testSet',repr(len(testSet)))

2. Similarity

We need to calculate the similarity between the two data, so that we can get the most similar N examples to make prediction.

Because the data on the four dimensions of flower measurement are all in digital form and have the same unit. We can use the Euclidean distance directly.

The Euclidean distance between two points a(x1,y1) and b(x2,y2) on a two-dimensional plane:

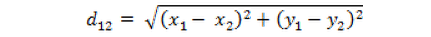
# length: tells the first few dimensions of the function to be processed, ignoring the latter
def euclideanDistance(instance1,instance2,length):
    distance = 0
    for x in range(length):
        distance += pow((instance1[x]-instance2[x]),2) #Addition of all dimension distances to be computed
    return math.sqrt(distance)

Test code:

data1 = [2,2,2,'a']
data2 = [4,4,4,'b']
# length=3 computes only the first three dimensions
distance = euclideanDistance(data1,data2,3)
print('distance',repr(distance))

3. Nearest Similarity

With the method of similarity calculation, we can get N data instances that are closest to the data that need to be predicted.

The most direct method is to calculate the distance between the data to be predicted and all data instances, and take N of the smallest distance among them.

# TesInstance: Data to be Predicted
def getNeighbors(trainingSet, testInstance, k):
    distances = []
    length = len(testInstance)-1
    for x in range(len(trainingSet)):
        #testinstance
        dist = euclideanDistance(testInstance, trainingSet[x], length)
        distances.append((trainingSet[x], dist))
        #distances.append(dist)
    distances.sort(key=operator.itemgetter(1))
    neighbors = []
    for x in range(k):
        neighbors.append(distances[x][0])
        return neighbors

Test code:

trainSet = [[2,2,2,'a'],[4,4,4,'b']]
testInstance = [5,5,5]
k = 1
neighbors = getNeighbors(trainSet,testInstance,k)
print(neighbors)

Test results (adjacent elements): [[4, 4, 4, 'b']]

4. Results

The next task is to get the prediction results based on several recent examples.

We can use these adjacent elements to vote on the predicted attributes, with the most voted option as the predicted result.

The following function implements the logic of voting, assuming that the attributes to be predicted are placed at the end of the data instance (array).

def getResponse(neighbors):
    classVotes = {}
    for x in range(len(neighbors)): #Traversing the nearest element
        response = neighbors[x][-1] #Assuming that the attributes to be predicted are at the end of the data instance (array)
        if response in classVotes:
            classVotes[response] += 1 # Voting for predictive attributes
        else:
            classVotes[response] = 1
    sortedVotes = sorted(classVotes.items(), key=None, reverse=True)
    return sortedVotes[0][0] #

Test code:

neighbors= [[1,1,1,'a'],[2,2,2,'a'],[3,3,3,'b']]
response = getResponse(neighbors)
print(response)

5. Accuracy

Simple evaluation method: Calculate the proportion of the correct prediction of the algorithm in the test data set, which is called classification accuracy.

# Assuming predictions are the predicted result set of the test set
def getAccuracy(testSet, predictions):
    correct = 0
    for x in range(len(testSet)):
        if testSet[x][-1] is predictions[x]:
            correct += 1
    return (correct/float(len(testSet))) * 100.0

Test code:

testSet = [[1,1,1,'a'],[2,2,2,'a'],[3,3,3,'b']]
predictions = ['a','a','a']
accuracy = getAccuracy(testSet,predictions)
print(accuracy)