1, Introduction to CART decision tree algorithm

CART (Classification And Regression Trees) algorithm is a tree construction algorithm, which can be used for both classification tasks and regression. Compared with ID3 and C4.5, which can only be used for discrete data and classification tasks, CART algorithm has a much wider application. It can be used for both discrete data and continuous data, and both classification and regression tasks can be processed.

This paper only discusses the construction of basic CART classification decision tree, not regression tree and pruning.

First of all, we should clarify the following points:
1. CART algorithm is a common method of binary classification. The decision tree generated by CART algorithm is a binary tree, while the decision tree generated by ID3 and C4.5 algorithm is a multi tree. From the perspective of operation efficiency, the binary tree model will be more efficient than the multi tree.
2. CART algorithm selects the optimal feature through Gini index.

2, Gini coefficient

Gini coefficient represents the impurity of the model. The smaller the Gini coefficient, the lower the impurity. Note that this is just opposite to the definition of information gain ratio in C4.5.

In the classification problem, assuming that there are k classes and the probability that the sample points belong to class k is pk, the Gini coefficient of the probability distribution is defined as:

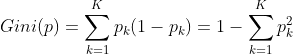
If CART is used for class II classification problems (not only for class II Classification), the Gini coefficient of probability distribution can be simplified to

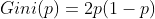
Assuming that feature A is used to divide data set D into two parts D1 and D2, the Gini coefficient of the data set divided according to feature A is:

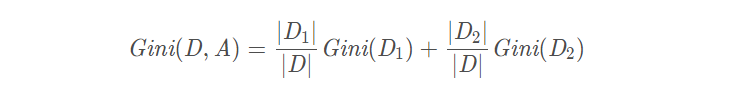
3, CART decision tree generation algorithm

Input: training data set D, conditions for stopping calculation
Output: CART decision tree
According to the training data set, starting from the root node, recursively perform the following operations on each node to build a binary decision tree:
(1) Calculate the Gini index of the existing features to the data set, as shown above;
(2) Select the feature corresponding to the minimum value of Gini index as the optimal feature, and the corresponding tangent point as the optimal tangent point (if there are multiple features or tangent points corresponding to the minimum value, just take one);
(3) According to the optimal features and optimal cut points, two sub nodes are generated from the current node, and the data in the training data set are allocated to the two sub nodes according to the features and attributes;
(4) Recursively call (1) (2) (3) to two child nodes until the stop condition is met.
(5) Generate CART tree.
Conditions for stopping the algorithm: the number of samples in the node is less than the predetermined threshold, or the Gini index of the sample set is less than the predetermined threshold (samples basically belong to the same class, if they all belong to the same class, it is 0), or the feature set is empty.
Note: the optimal tangent point is a necessary condition to divide the current sample into two classes (because we want to construct a binary tree). For the discrete case, the optimal tangent point is a value of the current optimal feature; For the continuous case, the optimal tangent point can be a specific value. In the specific application, we need to traverse all the possible optimal tangent points to find the optimal tangent point we need.

4, Python implementation of CART algorithm

from math import log
    
# Construct dataset
def create_dataset():
    dataset = [['youth', 'no', 'no', 'just so-so', 'no'],
               ['youth', 'no', 'no', 'good', 'no'],
               ['youth', 'yes', 'no', 'good', 'yes'],
               ['youth', 'yes', 'yes', 'just so-so', 'yes'],
               ['youth', 'no', 'no', 'just so-so', 'no'],
               ['midlife', 'no', 'no', 'just so-so', 'no'],
               ['midlife', 'no', 'no', 'good', 'no'],
               ['midlife', 'yes', 'yes', 'good', 'yes'],
               ['midlife', 'no', 'yes', 'great', 'yes'],
               ['midlife', 'no', 'yes', 'great', 'yes'],
               ['geriatric', 'no', 'yes', 'great', 'yes'],
               ['geriatric', 'no', 'yes', 'good', 'yes'],
               ['geriatric', 'yes', 'no', 'good', 'yes'],
               ['geriatric', 'yes', 'no', 'great', 'yes'],
               ['geriatric', 'no', 'no', 'just so-so', 'no']]
    features = ['age', 'work', 'house', 'credit']
    return dataset, features

# Calculates the Gini coefficient of the current set
def calcGini(dataset):
    # Find the total number of samples
    num_of_examples = len(dataset)
    labelCnt = {}
    # Traverse the entire sample set
    for example in dataset:
        # The tag value of the current sample is the last element of the list
        currentLabel = example[-1]
        # Count how many times each label appears
        if currentLabel not in labelCnt.keys():
            labelCnt[currentLabel] = 0
        labelCnt[currentLabel] += 1
    # After getting the number of samples of each label in the current set, calculate their p value
    for key in labelCnt:
        labelCnt[key] /= num_of_examples
        labelCnt[key] = labelCnt[key] * labelCnt[key]
    # Calculate Gini coefficient
    Gini = 1 - sum(labelCnt.values())
    return Gini
    
# Extract subset
# Function: first find all samples with axis tag value = value from the dataSet
# Then delete the axis tag value of these samples, and then extract them all into a new sample set
def create_sub_dataset(dataset, index, value):
    sub_dataset = []
    for example in dataset:
        current_list = []
        if example[index] == value:
            current_list = example[:index]
            current_list.extend(example[index + 1 :])
            sub_dataset.append(current_list)
    return sub_dataset

# Divide the current sample set into a part with value of feature i and a part with value other than value (two points)
def split_dataset(dataset, index, value):
    sub_dataset1 = []
    sub_dataset2 = []
    for example in dataset:
        current_list = []
        if example[index] == value:
            current_list = example[:index]
            current_list.extend(example[index + 1 :])
            sub_dataset1.append(current_list)
        else:
            current_list = example[:index]
            current_list.extend(example[index + 1 :])
            sub_dataset2.append(current_list)
    return sub_dataset1, sub_dataset2

def choose_best_feature(dataset):
    # Total number of features
    numFeatures = len(dataset[0]) - 1
    # When there is only one feature
    if numFeatures == 1:
        return 0
    # Initialize optimal Gini coefficient
    bestGini = 1
    # Initialize optimal features
    index_of_best_feature = -1
    # Traverse all features to find the optimal feature and the optimal tangent point under the feature
    for i in range(numFeatures):
        # De duplication, each attribute value is unique
        uniqueVals = set(example[i] for example in dataset)
        # Each value in the Gini dictionary represents the Gini coefficient after dividing the current set with the key corresponding to the value as the tangent point
        Gini = {}
        # For each value of the current feature
        for value in uniqueVals:
            # First find the two subsets divided by the value
            sub_dataset1, sub_dataset2 = split_dataset(dataset,i,value)
            # Find the proportion coefficient prob1 and prob2 of the two subsets in the original set
            prob1 = len(sub_dataset1) / float(len(dataset))
            prob2 = len(sub_dataset2) / float(len(dataset))
            # Calculate Gini coefficients for subset 1
            Gini_of_sub_dataset1 = calcGini(sub_dataset1)
            # Calculate Gini coefficients for subset 2
            Gini_of_sub_dataset2 = calcGini(sub_dataset2)
            # Calculate the final Gini coefficient divided by the current optimal tangent point
            Gini[value] = prob1 * Gini_of_sub_dataset1 + prob2 * Gini_of_sub_dataset2
            # Update the optimal features and optimal cut points
            if Gini[value] < bestGini:
                bestGini = Gini[value]
                index_of_best_feature = i
                best_split_point = value
    return index_of_best_feature, best_split_point
    
# Returns the value of the tag with the largest number of samples ('yes' or 'no')
def find_label(classList):
    # Initialize the dictionary for counting the times of each label
    # The key is each label, and the corresponding value is the number of times the label appears
    labelCnt = {}
    for key in classList:
        if key not in labelCnt.keys():
            labelCnt[key] = 0
        labelCnt[key] += 1
    # Sort classCount values in descending order
    # For example: sorted_labelCnt = {'yes': 9, 'no': 6}
    sorted_labelCnt = sorted(labelCnt.items(), key = lambda a:a[1], reverse = True)
    # There is a problem with the following way of writing
    # sortedClassCount = sorted(labelCnt.iteritems(), key=operator.itemgetter(1), reverse=True)
    # Sorted_ The first value of the first element in labelcnt is the desired value
    return sorted_labelCnt[0][0]
    
    
def create_decision_tree(dataset, features):
    # Find the labels of all samples in the training set
    # For the initial dataset, its label_list = ['no', 'no', 'yes', 'yes', 'no', 'no', 'no', 'yes', 'yes', 'yes', 'yes', 'yes', 'yes', 'yes', 'no']
    label_list = [example[-1] for example in dataset]
    # First write two cases where recursion ends:
    # If the labels of all samples in the current set are equal (that is, the samples have been classified as "pure")
    # The label value is directly returned as a leaf node
    if label_list.count(label_list[0]) == len(label_list):
        return label_list[0]
    # If all features of the training set have been used, there are no available features, but the sample has not been classified as "pure"
    # The label with the most samples is returned as the result
    if len(dataset[0]) == 1:
        return find_label(label_list)
    # The following is the formal establishment process
    # Select the subscript and the best segmentation point of the best feature for branching
    index_of_best_feature, best_split_point = choose_best_feature(dataset)
    # Get the best feature
    best_feature = features[index_of_best_feature]
    # Initialize decision tree
    decision_tree = {best_feature: {}}
    # Delete the current best feature after it has been used
    del(features[index_of_best_feature])
    # Sub feature = current feature (because the used feature has been deleted just now)
    sub_labels = features[:]
    # Recursive call to create_decision_tree to generate new nodes
    # Generate a binary set divided by the optimal tangent point
    sub_dataset1, sub_dataset2 = split_dataset(dataset,index_of_best_feature,best_split_point)
    # Construct left subtree
    decision_tree[best_feature][best_split_point] = create_decision_tree(sub_dataset1, sub_labels)
    # Construct right subtree
    decision_tree[best_feature]['others'] = create_decision_tree(sub_dataset2, sub_labels)
    return decision_tree
    
# Use the decision tree trained above to classify the new samples
def classify(decision_tree, features, test_example):
    # The attribute represented by the root node
    first_feature = list(decision_tree.keys())[0]
    # second_dict is the value of the first classification attribute (also a dictionary)
    second_dict = decision_tree[first_feature]
    # The position of the attribute represented by the tree root in the attribute tag, that is, the first attribute
    index_of_first_feature = features.index(first_feature)
    # For second_ Every key in Dict
    for key in second_dict.keys():
        # key not equal to 'others'
        if key != 'others':
            if test_example[index_of_first_feature] == key:
            # If current second_ The value of the key of dict is a dictionary
                if type(second_dict[key]).__name__ == 'dict':
                    # Recursive query is required
                    classLabel = classify(second_dict[key], features, test_example)
                # If current second_ The value of the key of dict is a separate value
                else:
                    # Is the tag value to find
                    classLabel = second_dict[key]
            # If the value of the test sample in the current feature is not equal to key, it means that its value in the current feature belongs to 'others'
            else:
                # If second_ If the value of dict ['others'] is a string, it is output directly
                if isinstance(second_dict['others'],str):
                    classLabel = second_dict['others']
                # If second_ If the value of dict ['others'] is a dictionary, the query is recursive
                else:
                    classLabel = classify(second_dict['others'], features, test_example)
    return classLabel
    
if __name__ == '__main__':
    dataset, features = create_dataset()
    decision_tree = create_decision_tree(dataset, features)
    # Print the generated decision tree
    print(decision_tree)
    # Classify the new samples
    features = ['age', 'work', 'house', 'credit']
    test_example = ['midlife', 'yes', 'no', 'great']
    print(classify(decision_tree, features, test_example))

If it is a binary classification problem, then the functions calcGini and choose_ best_ Features can be simplified as follows:

# Calculate the probability p that the sample belongs to the first class
def calcProbabilityEnt(dataset):
    numEntries = len(dataset)
    count = 0
    label = dataset[0][len(dataset[0]) - 1]
    for example in dataset:
        if example[-1] == label:
            count += 1
    probabilityEnt = float(count) / numEntries
    return probabilityEnt

def choose_best_feature(dataset):
    # Total number of features
    numFeatures = len(dataset[0]) - 1
    # When there is only one feature
    if numFeatures == 1:
        return 0
    # Initialize optimal Gini coefficient
    bestGini = 1
    # Initialize optimal features
    index_of_best_feature = -1
    for i in range(numFeatures):
        # De duplication, each attribute value is unique
        uniqueVals = set(example[i] for example in dataset)
        # Gini coefficient that defines the value of the characteristic
        Gini = {}
        for value in uniqueVals:
            sub_dataset1, sub_dataset2 = split_dataset(dataset,i,value)
            prob1 = len(sub_dataset1) / float(len(dataset))
            prob2 = len(sub_dataset2) / float(len(dataset))
            probabilityEnt1 = calcProbabilityEnt(sub_dataset1)
            probabilityEnt2 = calcProbabilityEnt(sub_dataset2)
            Gini[value] = prob1 * 2 * probabilityEnt1 * (1 - probabilityEnt1) + prob2 * 2 * probabilityEnt2 * (1 - probabilityEnt2)
            if Gini[value] < bestGini:
                bestGini = Gini[value]
                index_of_best_feature = i
                best_split_point = value
    return index_of_best_feature, best_split_point

5, Operation results