data structure
What is a data structure?
Simply put, data structure is to design how data is organized and stored in a computer.
Lists, collections and dictionaries are all data structures.
N.Wirth: "Program = Data Structure + Algorithms"
list
List: In other programming languages, called "arrays", is a basic data structure type.
Questions about lists:
- How do the elements in the list be stored?
- What basic operations does the list provide?
- What is the time complexity of these operations?
Stack
Stack is a collection of data that can be understood as a list of insertions or deletions that can only be performed at one end.
Stack features:
- last-in, first-out
The concept of stack:
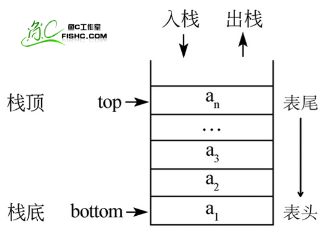
- Top of stack
- Bottom of stack
The basic operation of the stack:
- Stack (stack): push
- Stack: pop
- Take the top of the stack: gettop
Pictured:
Python implementation of stack:
You don't need to define it yourself, just use the list structure. Stack function: append Out-of-stack function: pop Look at the top stack function: li[-1]
Application of stack - bracket matching problem:
Bracket matching problem: Give a string, which contains parentheses, middle parentheses, braces, to find whether the brackets in the string match.
For example:
()() () []{} matching
([{()}]) Matching
[] (mismatch)
[(]) Mismatch
Code:
def cheak_kuohao(s):
stack = []
for char in s:
if char in {'(','[', '{'}:
stack.append(char)
elif char == ')':
if len(stack)>0 and stack[-1]=='(':
stack.pop()
else:
return False
elif char == ']':
if len(stack) > 0 and stack[-1] == '[':
stack.pop()
else:
return False
elif char == '}':
if len(stack)>0 and stack[-1]=='{':
stack.pop()
else:
return False
if len(stack) == 0:
return True
else:
return False
print(cheak_kuohao('()[]{{[]}}'))
# True
The application of stack-maze problem:
Give a two-dimensional list of mazes (0 for channels, 1 for walls). Give an algorithm to find a way out of the maze

Solutions:
On a maze node (x,y), four directions can be explored: maze [x-1] [y], maze [x+1] [y], maze [x] [y-1], maze [x] [y-1], maze [x] [y+1] Idea: Start from a node, arbitrarily find the next point to go, when you can not find the point to go, go back to the last point to find whether there are other directions. Method: Create an empty stack, first put the entry position into the stack. When the stack is not empty, loop: get the top element of the stack, look for the next travelable adjacent square. If you can't find the next travelable adjacent square, it shows that the current position is a dead end, and go back (that is, the current position is out of the stack, see if there is another way out of the front point).
Solution code:
maze = [
[1,1,1,1,1,1,1,1,1,1],
[1,0,0,1,0,0,0,1,0,1],
[1,0,0,1,0,0,0,1,0,1],
[1,0,0,0,0,1,1,0,0,1],
[1,0,1,1,1,0,0,0,0,1],
[1,0,0,0,1,0,0,0,0,1],
[1,0,1,0,0,0,1,0,0,1],
[1,0,1,1,1,0,1,1,0,1],
[1,1,0,0,0,0,0,1,0,1],
[1,1,1,1,1,1,1,1,1,1]
]
dirs = [lambda x, y: (x + 1, y),
lambda x, y: (x - 1, y),
lambda x, y: (x, y - 1),
lambda x, y: (x, y + 1)]
def mpath(x1, y1, x2, y2):
stack = []
stack.append((x1, y1))
while len(stack) > 0:
curNode = stack[-1]
if curNode[0] == x2 and curNode[1] == y2:
#Reach the finish line
for p in stack:
print(p)
return True
for dir in dirs:
nextNode = dir(curNode[0], curNode[1])
if maze[nextNode[0]][nextNode[1]] == 0:
#Find the next one
stack.append(nextNode)
maze[nextNode[0]][nextNode[1]] = -1 # Mark as past to prevent dead cycles
break
else:#Four directions were not found.
maze[curNode[0]][curNode[1]] = -1 # A dead end. Don't go next time.
stack.pop() #To flash back
print("No road")
return False
mpath(1,1,8,8)
queue
Queue is a data set that allows insertion only at one end of the list and deletion at the other end.
The end of the insertion is called rear, and the insertion action is called entry or entry.
The end of the deletion is called the front, and the deletion action is called out of the team.
The nature of the queue:
- First-in, First-out
Two-way queue:
- Entry and exit operations are allowed at both ends of the queue
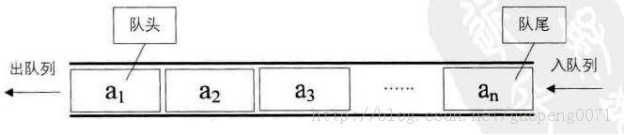
Can queues be simply implemented in lists? Why?
Preliminary assumption: list + two subscript pointers
Create a list and two variables, the front variable points to the head of the queue, and the rear variable points to the end of the queue.
Initially, both front and rear are 0.
Entry operation: The element is written to the position of li[rear], rear increases by 1.
Out-of-line operation: Returns the element of li[front], and the front decreases by 1.
The question of this realization? (No, it takes time or memory)
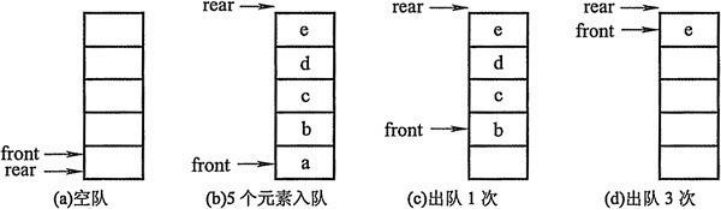
Improvement: Logically connect the beginning and end of the list
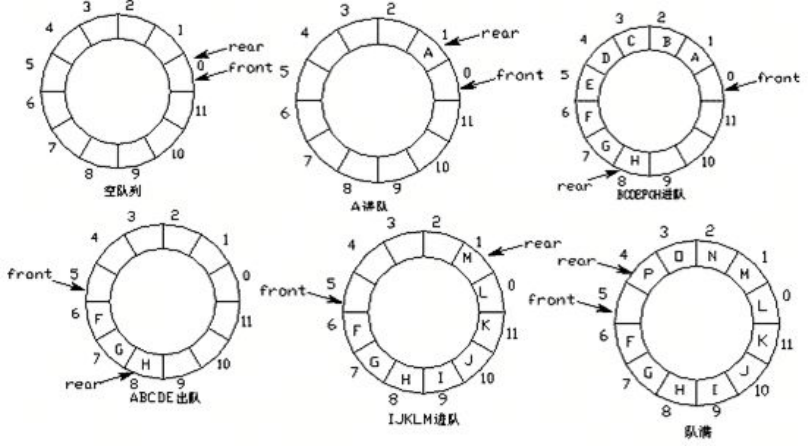

1 ring queue: When the end of the queue pointer front = Maxsize + 1, another forward position automatically goes to 0. 2. Implementation: Residual arithmetic 3 Team Head Pointer Forward 1:front = front + 1% MaxSize Four trailing pointers forward 1:rear = rear + 1% MaxSize 5 Team Air Conditions: rear = front 6 Teams Full Conditions: (rear + 1)% MaxSize = front
python usage: (from collections import deque)
Create queues: queue = deque(li) Entry: append Team formation: popleft The first two-way queue: appendleft Two-way queue at the end of the queue: pop
Application of Queue-Maze Problem
Solutions:
Idea: Start from a node, find all the points that can continue to go below. Keep looking until you find the exit. Method: Create an empty queue and put the starting point into the queue. Not a space-time loop in the queue: once out of the queue. If the current position is the exit, the algorithm is terminated; otherwise, four adjacent blocks of the current square can be found and all of them enter the queue.
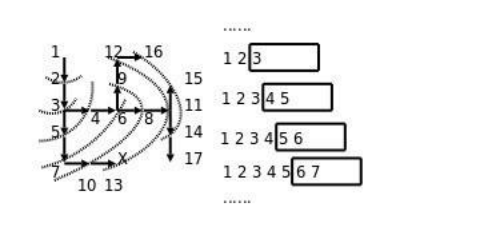
Code:
from collections import deque
mg = [
[1,1,1,1,1,1,1,1,1,1],
[1,0,0,1,0,0,0,1,0,1],
[1,0,0,1,0,0,0,1,0,1],
[1,0,0,0,0,1,1,0,0,1],
[1,0,1,1,1,0,0,0,0,1],
[1,0,0,0,1,0,0,0,0,1],
[1,0,1,0,0,0,1,0,0,1],
[1,0,1,1,1,0,1,1,0,1],
[1,1,0,0,0,0,0,1,0,1],
[1,1,1,1,1,1,1,1,1,1]
]
dirs = [lambda x, y: (x + 1, y),
lambda x, y: (x - 1, y),
lambda x, y: (x, y - 1),
lambda x, y: (x, y + 1)]
def print_p(path):
curNode = path[-1]
realpath = []
print('The maze path is:')
while curNode[2] != -1:
realpath.append(curNode[0:2])
curNode = path[curNode[2]]
realpath.append(curNode[0:2])
realpath.reverse()
print(realpath)
def mgpath(x1, y1, x2, y2):
queue = deque()
path = []
queue.append((x1, y1, -1))
while len(queue) > 0:
curNode = queue.popleft()
path.append(curNode)
if curNode[0] == x2 and curNode[1] == y2:
#Reach the finish line
print_p(path)
return True
for dir in dirs:
nextNode = dir(curNode[0], curNode[1])
if mg[nextNode[0]][nextNode[1]] == 0: # Find the next box
queue.append((*nextNode, len(path) - 1))
mg[nextNode[0]][nextNode[1]] = -1 # Marked as past
return False
mgpath(1,1,8,8)
Single linked list
Each element in the list is an object, and each object is called a node, which contains the data field key and the next pointer to the next node. Through the interconnection of each node, a linked list is finally concatenated in series.
Node definitions:
class Node(object):
def __init__(self, item):
self.item = item
self.next = None
a = Node(10)
b = Node(20)
c = Node(30)
a.next = b
b.next =c
Head node:

Traversal list:
def traversal(head):
curNode = head # Temporary pointer
while curNode is not None:
print(curNode.item)
curNode = curNode.next
You can only find the number from the front, but not from the front.
Insert:
p.next = curNode.next curNode.next = p
Delete:
p = curNode.next curNode.next = curNode.next.next del p
Create linked list
Head insertion:
def createLinkListF(li):
l = Node()
for num in li:
s = Node(num)
s.next = l.next
l.next = s
return l
Tail insertion method:
def createLinkListR(li):
l = Node()
r = l #r points to tail node
for num in li:
s = Node(num)
r.next = s
r = s
Double linked list
Each node in the double linked list has two pointers: one pointing to the back node and one pointing to the front node.
Node definitions:
class Node(object):
def __init__(self, item=None):
self.item = item
self.next = None
self.prior = None
Head node:
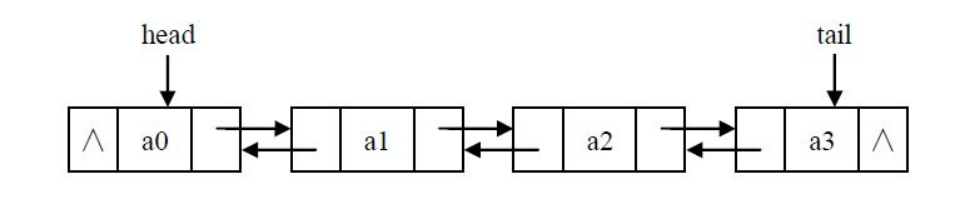
Insert:
p.next = curNode.next curNode.next.prior = p p.prior = curNode curNode.next = p
Delete:
p = curNode.next curNode.next = p.next p.next.prior = curNode del p
Establishing Double Link List
Tail insertion method:
def createLinkListR(li):
l = Node()
r = l
for num in li:
s = Node(num)
r.next = s
s.prior = r
r = s
return l, r
Collections and Dictionaries in Python
Hash Table, also known as Hash Table, is a storage structure of linear tables. By using the keyword K of each object as an independent variable and through a hash function h(k), K is mapped to the subscript h(k), and the object is stored in this location.
For example: data set {1,6,7,9}, assuming that there exists a hash function h(x) such that h(1) = 0, h(6) = 2, h(7) = 4, h(9) = 5, the hash table is stored as [1,None, 6, None, 7, 9].
When we look for the location of element 6, we get the subscript (h(6) = 2) of the element through the hash function h(x), so we can find the element at 2 locations.
There are many kinds of hash functions, so we don't do further research here.
Hash conflict: Because the subscript range of hash table is limited and the value of element keyword is nearly infinite, it may occur that h(102) = 56, h(2003) = 56. At this point, two elements are mapped to the same subscript, resulting in hash conflicts.
Resolving the Hashi conflict:
- Zipper method links all conflicting elements with linked list
- Open Addressing Method Gets New Address by Hash Conflict Function
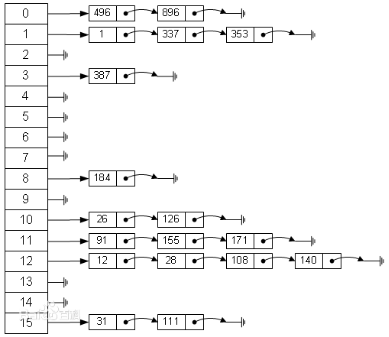
Dictionaries in Python:
A = {name':'Alex','age': 18,'gender':'Man'} uses a hash table to store the dictionary and maps the keys of the dictionary to subscripts through a hash function. Assuming that h('name') = 3, h('age') = 1, h('gender') = 4, the hash table is stored as [None, 18, None,'Alex','Man']
When the number of keys in a dictionary is small, there will be almost no hash collision, and the time complexity of finding an element is O(1).
