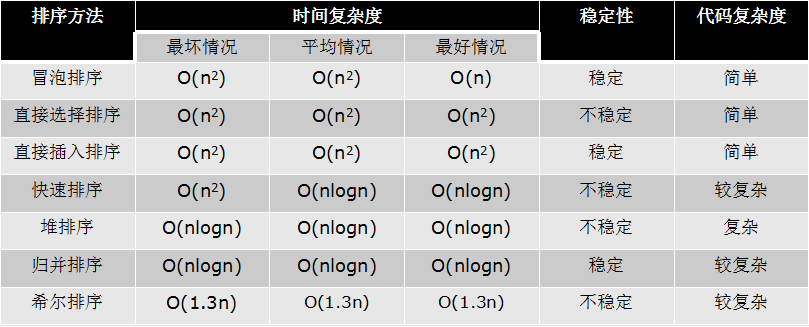
Heap sort

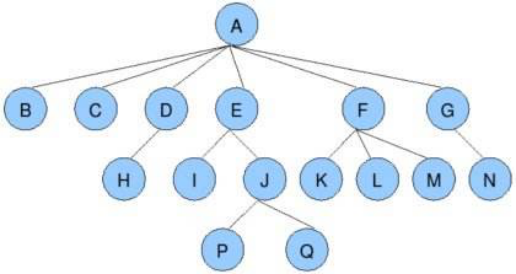
1. Introduction of Trees and Binary Trees

A tree is a data structure such as a directory structure.

Tree is a data structure that can be defined recursively

A tree is a set of n nodes:

• If n=0, then this is an empty tree.
• If n > 0, there is one node as the root node of the tree, and the other nodes can be divided into m sets, each set itself is a tree.

Some concepts

• Root node,
• Leaf node
• Tree depth (height)
• Degree of tree
• Child node/parent node
• subtree

Pictured:

2. Binary Tree

Binary Trees: Trees with a degree not exceeding 2 (nodes have at most two forks)

Pictured:

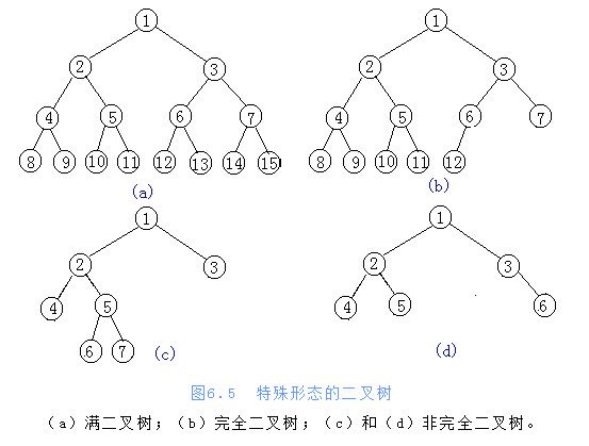
3. Two Special Binary Trees

• Full two fork tree
• Complete Binary Tree

Pictured:

4. Storage of Binary Tree

• Chain Storage
• Sequential storage (list)

Pictured:

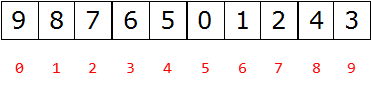
What is the relationship between the number subscript of the parent node and the left child node?

• 0-1 1-3 2-5 3-7 4-9

• i ~ 2i+1

What is the relationship between the number subscript of the parent node and the right child node?

• 0-2 1-4 2-6 3-8 4-10

• i – 2i+2

5, heap

Heap:

• Big Rootstock: A complete binary tree that satisfies any node larger than its child node
• Rootstock: A complete binary tree that satisfies any node smaller than its child node

Big root pile:

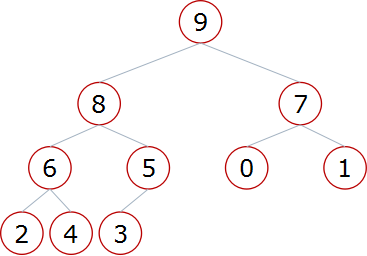
Little root pile:

6. Heap sorting process

1. Build heap
2. Get the top element.
3. To remove the top of the heap for the largest element, the last element of the heap is placed on the top of the heap, and the heap can be reordered by one adjustment.
4. Top element is the second largest element
5. Repeat step 3 until the heap empties.

7. Structural Reactor

def sift(data,low,high):
    #The root node of low to adjust the scope
    #The last node of the entire high data
    i = low
    j = 2 * i  + 1  #left child
    tmp = data[i]  #Go out and follow the node
    while j <= high:   #The left child is on the list, indicating that i have children.
        if j+1 <= high and data[j] < data[j+1]:      #If there is a right child and the right child is older than the left child
            j = j + 1
        if data[j] > tmp:
            data[i] = data[j]
            i = j
            j = 2 *i +1
        else:
            break
    data[i] = tmp

def heap_sort(data):
    n = len(data)
    for i  in range(n//2-1, -1, -1): # n//2-1 fixed usage
        sift(data,i,n-1)                # Structural pile

8. Heap Sorting

Complete code:

import time
import random

def call_time(func):
    def inner(*args,**kwargs):
        t1 = time.time()
        re = func(*args,**kwargs)
        t2 = time.time()
        print('Time cost:',func.__name__,t2-t1)
        return re
    return inner

def sift(data,low,high):
    #The root node of low to adjust the scope
    #The last node of the entire high data
    i = low
    j = 2 * i  + 1  #left child
    tmp = data[i]  #Go out and follow the node
    while j <= high:   #The left child is on the list, indicating that i have children.
        if j+1 <= high and data[j] < data[j+1]:      #If there is a right child and the right child is older than the left child
            j = j + 1
        if data[j] > tmp:
            data[i] = data[j]
            i = j
            j = 2 *i +1
        else:
            break
    data[i] = tmp

@call_time
def heap_sort(data):
    n = len(data)
    for i  in range(n//2-1, -1, -1): # n//2-1 fixed usage
        sift(data,i,n-1)                # Structural pile

    for i in range(n):              # Number one at a time in n cycles
        data[0],data[n-1-i] = data[n-1-i],data[0]
        sift(data,0,n-1-i-1)

data = list(range(10000))
random.shuffle(data)

heap_sort(data)
# Time cost: heap_sort 0.08801126480102539

Time complexity: O(nlogn)

Merge sort

Combine two ordered lists into an ordered list

Example:

[2,5,7,8,91,3,4,6]

Train of thought:

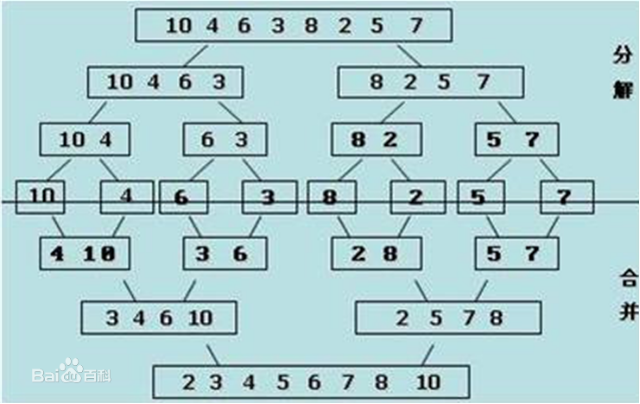
Decomposition: The smaller the list, the smaller it will be until it is broken into one element

An element is ordered

Merge: Merge two ordered lists, and the list gets bigger and bigger

Code:

import time
import random

def call_time(func):
    def inner(*args,**kwargs):
        t1 = time.time()
        re = func(*args,**kwargs)
        t2 = time.time()
        print('Time cost:',func.__name__,t2-t1)
        return re
    return inner

def merge(li, low, mid, high):
    i = low
    j = mid + 1
    ltmp = []
    while i <= mid and j <= high:
        if li[i] < li[j]:
            ltmp.append(li[i])
            i += 1
        else:
            ltmp.append(li[j])
            j += 1
    while i <= mid:
        ltmp.append(li[i])
        i += 1
    while j <= high:
        ltmp.append(li[j])
        j += 1
    li[low:high+1] = ltmp


def _mergesort(li, low, high):
    if low < high:
        mid = (low + high) // 2
        _mergesort(li,low, mid)
        _mergesort(li, mid+1, high)
        merge(li, low, mid, high)

@call_time
def mergesort(li):
    _mergesort(li, 0, len(li) - 1)

data = list(range(10000))
random.shuffle(data)

mergesort(data)
# Time cost: mergesort 0.0835103988647461

Time complexity: O(nlogn)

Shell Sort

Hill sorting is a grouping insertion sorting algorithm.

Firstly, an integer d1=n/2 is selected and the elements are divided into D1 groups. The distance between adjacent elements in each group is d1, and the elements are inserted and sorted directly in each group.

Take the second integer d2=d1/2 and repeat the grouping sorting process until di=1, that is, all elements are directly inserted into the same group.

Hill sort does not make certain elements ordered, but makes the whole data more and more close to ordering; the last sort makes all data ordered.

Code:

import time
import random

def call_time(func):
    def inner(*args,**kwargs):
        t1 = time.time()
        re = func(*args,**kwargs)
        t2 = time.time()
        print('Time cost:',func.__name__,t2-t1)
        return re
    return inner

@call_time
def shell_sort(li):
    gap = len(li) // 2
    while gap >= 1:
        for i in range(gap, len(li)):
            tmp = li[i]
            j = i - gap
            while j >= 0 and tmp < li[j]:
                li[j + gap] = li[j]
                j -= gap
            li[j + gap] = tmp
        gap = gap // 2

data = list(range(10000))
random.shuffle(data)

shell_sort(data)
# Time cost: shell_sort 0.1275160312652588

Time complexity: O(nlogn)

Quick sort, heap sort, merge sort comparison:

The time complexity of the three sorting algorithms is O(nlogn)

Generally speaking, in terms of running time:

• Quick Sort < Merge Sort < Heap Sort

The disadvantages of the three sorting algorithms are as follows:

• Quick Sorting: Low Sorting Efficiency in Extreme Conditions
• Merge sort: additional memory overhead
• Heap sorting: relatively slow in fast sorting algorithms

Comparing time:

quick_sort(data1)    # Quick row
heap_sort(data2)     # Heap row
mergesort(data3)     # Return row
sys_sort(data4)        #System comes with

# Time cost: quick_sort 0.053006649017333984
# Time cost: heap_sort 0.08601117134094238
# Time cost: mergesort 0.08000993728637695
# Time cost: sys_sort 0.004500627517700195

View: