1. What is a stack?

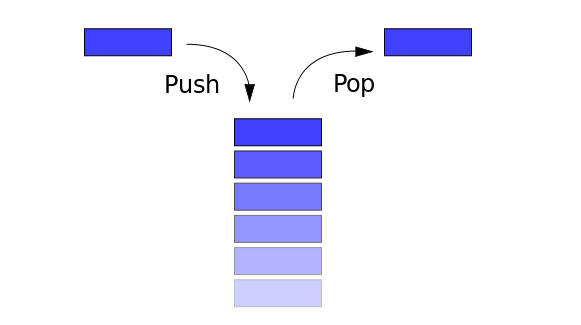
   Stack is a first in, first out memory, which can only access data items through one entry. A linear table that is restricted to insert and delete operations only at the end of the table. This end is called the top of the stack, and the other end is called the bottom of the stack. Inserting new elements into a stack is also called pushing, pushing or pressing. It is to put new elements on top of the stack to make it a new stack top element. Deleting elements from a stack is also called pushing out or pushing back. It is to delete the stack top elements and make the adjacent elements become new stack top elements.
   

2. How to implement stack and its basic operation in Python?
   Compared with C and C + +, the data structure in Python is so simple that the underlying implementation does not need to call the function corresponding to the corresponding operation of each data structure. The following code snippet is its underlying implementation.

```python
class Stcak:
    def __init__(self):
        self.items = []
    #Judge whether the stack is empty
    def inEmpty(self):
        return self.items ==[]  #Is the element in the stack empty
    #Pressing elements into the stack
    def push(self,item):
        self.items.append(item)
    #Element stack
    def pop(self):
        return self.items.pop()
    #Take out the element at the bottom of the stack
    def peek(self):
        return self.items[len(self.items) - 1]
    #Get the length of the stack
    def size(self):
        return len(self.items)

1. Some examples of stack applications:
   3.1 implement universal bracket matching algorithm:
   Problem background: in the process of actual programming, we need to judge whether the left and right half brackets of the superimposed brackets are complete, and whether the tags and end tags in html are complete. For this kind of problem, we can solve it by stack operation.

from pythonds.basic.stack import Stack
def parChecker(SymbolString):
    #Create a new stack
    s = Stack()
    #Whether the initial state of balance is set to True
    balanced = True
    index = 0
    while index < len(SymbolString) and balanced:
        #Traverse from the first symbol
        symbol = SymbolString[index]
        #If it's one of the three symbols, stack
        if symbol in "([{":
            s.push(symbol)
        else:
            #If not, judge whether the stack is empty
            if s.isEmpty():
                balanced = False
            else:
                top = s.pop()
                #If the element still exists and is inconsistent with the element, it indicates that there is a single bracket
                if not matches(top,symbol):
                    balanced = False
        index = index + 1
    if balanced and s.isEmpty():
        return True
    else:
        return False
def matches(open,close):
    open = "([{"
    close = "}])"
    return open.index(open) == close.index(close)
print(parChecker('[{[{()}]}]'))
print(parChecker('[{[{]]]'))

class Stack(object):
    def __init__(self, limit=10):
        self.stack = [] #Storage elements
        self.limit = limit #Stack capacity limit
    def push(self, data): #Determine whether the stack overflows
        if len(self.stack) >= self.limit:
            print('StackOverflowError')
            pass
        self.stack.append(data)
    def pop(self):
        if self.stack:
            return self.stack.pop()
        else:
            raise IndexError('pop from an empty stack') #Empty stack cannot be ejected
    def peek(self): #View the top element of the stack
        if self.stack:
            return self.stack[-1]
    def is_empty(self): #Judge whether the stack is empty
        return not bool(self.stack)
    def size(self): #Return stack size
        return len(self.stack)
def balanced_parentheses(parentheses):
    stack = Stack(len(parentheses))
    for parenthesis in parentheses:
        if parenthesis == '(':
            stack.push(parenthesis)
        elif parenthesis == ')':
            if stack.is_empty():
                return False
            stack.pop()
    return stack.is_empty()
if __name__ == '__main__':
    examples = ['((()))', '((())', '(()))']
    print('Balanced parentheses demonstration:\n')
    for example in examples:
        print(example + ': ' + str(balanced_parentheses(example)))

3.2 realization of conversion from decimal number to N-base number
Background: to convert a decimal number into an n-ary number, you only need to remove N and then take the remainder until the remainder is zero, and then reverse the remainder to get the n-ary number. The implementation code of this process is as follows:

from pythonds.basic.stack import Stack
def baseConverter(decNum, base):
    digits = "0123456789ABCDEF"
    remstack = Stack()
    while decNum > 0:
        rem = decNum % base
        remstack.push(rem)
        decNum = decNum // base
    newString = ""
    while not remstack.isEmpty():
        newString = newString + digits[remstack.pop()]
    return newString
print(baseConverter(25,2))
print(baseConverter(25,16))

3.3 change expression from middle order traversal to post order traversal
For example, A+(B+CD) can be expressed as ABCD + +, and its implementation code is as follows:

from pythonds.basic.stack import Stack
def infixToPostfix(infixexpr):
    #Define priorities
    prec = {}
    prec["*"] = 3
    prec["/"] = 3
    prec["+"] = 2
    prec["-"] = 2
    prec["("] = 1
    opStack = Stack()
    postfixlist = []
    #Split the statement into a listbit (), parse the expression to the word list
    tokenList = infixexpr.split()
    for token in tokenList:
        if token in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or token in "0123456789":
            postfixlist.append(token)
        elif token == "(":
            opStack.push(token)
        elif token == ")":
            topToken = opStack.pop()
            while topToken != '(':
                postfixlist.append(topToken)
                topToken = opStack.pop()
        else:
            while (not opStack.isEmpty()) and \
                    (prec[opStack.peek()] >= prec[token]):
                    postfixlist.append(opStack.pop())
            opStack.push(token)
    while not opStack.isEmpty():
        postfixlist.append(opStack.pop())
    return " ".join(postfixlist)
print(infixToPostfix('(V*A)+(B*C)'))

1. summary
   In a word, stack is a kind of linear data structure, which can be used to judge symmetry and inversion problems. Common functions such as pop, push and append are also very simple to implement. Today's content is basically like this. I hope it can help you to learn the data structure.