Sequence table

Storage method of elements in the sequence table:

The complete information of the sequence table consists of two parts:
1. Set of elements in the table
2. Information on the overall situation of the table

There are two ways to implement the sequence table:

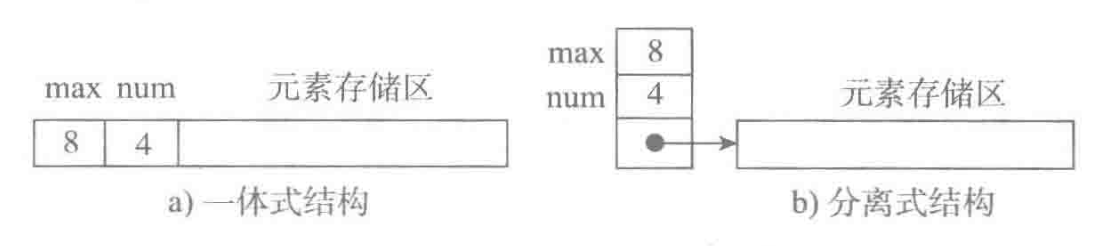
1. Figure a shows an integrated structure: table information and element storage areas are continuously stored in memory. The structure has strong integrity and is easy to manage, but the element storage area is fixed after creating the sequence table.
2. Figure b shows a separate structure: the table object only has information about the whole table, and the element storage area is associated with the basic table object through links.
3. When replacing the element storage area: the whole table needs to be changed to replace the data area of the integrated structure. Separate type only needs to change the data area pointer
4. When expanding the element storage area: the separate type can expand the data area without changing the table object (this implementation method is called dynamic sequential table)
   Two strategies for expansion:
   • Each expansion adds a fixed number of storage locations (linear growth). Features: save space. If the expansion operation is frequent, the operation times are more.
   • Double the capacity each time. Features: reduce the number of expansion operations, exchange space for time, recommended.

Sequence table operation complexity
Add element:
a. Add elements at the end, and the time complexity is O(1)
b. Non order preserving added elements (the element is added to the target position, and the element where the target position is located is moved to the end of the table), and the time complexity is O(1)
c. Order preserving elements are added, and the time complexity is O(n)

Delete element:
a. Delete the footer element. The time complexity is O(1)
b. Non order preserving element deletion (uncommon, similar to adding element B), with time complexity of O(1)
c. The order preserving element is deleted, and the time complexity is O(n)

Sequential tables in Python

list and tuple are implemented by sequential table

Basic implementation of list

list is a kind of dynamic sequence table implemented by separate technology
Official implementation of Python:
1. list creates an empty table (or a very small table), and the system allocates a storage area that can hold 8 elements;
2. If the element storage area is full, a storage area four times as large. When the threshold value is 50000, double it (avoid too many free areas)

Linked list

Single linked list operation

is_empty() whether the linked list is empty
length() linked list length
travel() traverses the entire linked list
add(item) adds an element to the header of the linked list
append(item) adds an element at the end of the linked list
insert(pos, item) adds an element at the specified location
remove(item) deletes a node
search(item) finds whether the node exists

Single linked list implementation

class SingleNode(object):
    """Node of single linked list"""

    def __init__(self, item):
        # _ item stores data elements
        self.item = item
        # _ Next is the identification of the next node
        self.next = None
class SingleLinkList(object):
    "Single linked list"

    def __init__(self):
        self._head = None
    def is_empty(self):
        "Determine whether the linked list is empty"
        return self._head == None
    def length(self):
        "Linked list length"
        p = self._head
        count = 0
        while p!=None:
            count+=1
            p = p.next
        return count
    def travel(self):
        "Traversal linked list,Returns all values as a list"
        p = self._head
        items = []
        while p!=None:
            items.append(p.item)
            p = p.next

        return items
    def add(self,item):
        "Insert element by header"
        node = SingleNode(item)
        node.next = self._head
        self._head = node
    def append(self,item):
        node = SingleNode(item)
        p = self._head
        if p != None:
            while p.next!=None:
                p = p.next
        else:
            print("error")
            return None
        p.next = node
    def insert(self,pos,item):
        """Add element at specified location"""
        # If the specified position pos is before the first element, header insertion is performed
        if pos <= 0:
            self.add(item)
        # If the specified position exceeds the tail of the linked list, the tail insertion is performed
        elif pos > (self.length() - 1):
            self.append(item)
        # The specified location was found
        else:
            node = SingleNode(item)
            count = 0
            # pre is used to point to the previous position pos-1 of the specified position POS, and initially move from the original node to the specified position
            pre = self._head
            while count < (pos - 1):
                count += 1
                pre = pre.next
            # First point the next of the new node to the node at the insertion location
            node.next = pre.next
            # Point the next of the previous node at the insertion location to the new node
            pre.next = node

    def remove(self,item):
        """Delete node"""
        cur = self._head
        pre = None
        while cur != None:
            # The specified element was found
            if cur.item == item:
                # If the first is the deleted node
                if not pre:
                    # Point the header pointer to the next node of the header node
                    self._head = cur.next
                else:
                    # Point the next node before the deletion location to the next node after the deletion location
                    pre.next = cur.next
                break
            else:
                # Continue to move the node backward according to the linked list
                pre = cur
                cur = cur.next
    def search(self,item):
        p = self._head
        while p!=None:
            if p.item == item:
                return True
            p = p.next
        return False

if __name__ == "__main__":
    ll = SingleLinkList()
    ll.add(1)
    ll.add(2)
    ll.append(3)
    ll.insert(2, 4)
    print("length:",ll.length())
    print(ll.travel())
    print(ll.search(3))
    print (ll.search(5))
    ll.remove(1)
    print ("length:",ll.length())
    print(ll.travel())