brief introduction

From: Easy to understand and explain linked list
One way linked list:

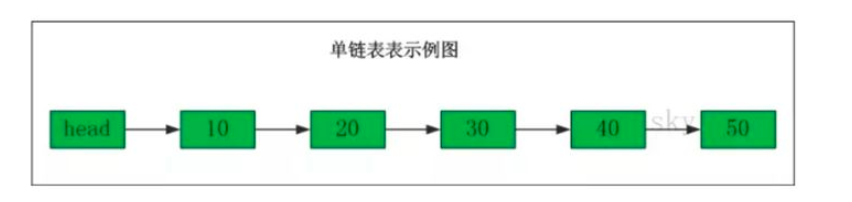
Bidirectional linked list:

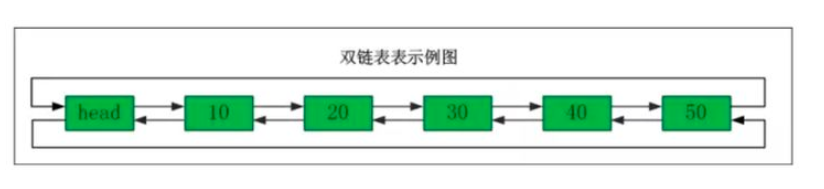
Look at the picture and understand...

Bidirectional linked list data structure

From:
Data structure - bidirectional linked list (Python Implementation)
Data structure has always been a very important part in the programming world. Whether it is development or algorithm, even for interview, data structure is a required course. Today, we introduce a kind of linked list - the code implementation of two-way linked list.

Bidirectional linked list:

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None
        self.prev = None
    def getData(self):
        return self.data

    def setData(self, data):
        self.data = data

    def getNext(self):
        return self.next

    def getPrev(self):
        return self.prev

OK, we define the node class and implement the methods of obtaining, modifying node data and obtaining the previous / next node.
You can instantiate a node by node = Node(10).

Next, let's define the linked list class:

class TwoWayList:
    def __init__(self):
        self.head = None
        self.tail = None
        self.length = 0

OK, we define a linked list class and set three properties. Head represents the head node, tail represents the tail node, and length represents the length of the linked list. Next, we add some methods to the linked list class.

1. Judge whether the linked list is empty:

def isEmpty(self):
        return self.head == None

1. Add a node at the end of the linked list:

def append(self, item):
        if self.length == 0:
            node = Node(item)
            self.head = node
            self.tail = node
            self.length = 1
            return
        node = Node(item)
        tail = self.tail
        tail.next = node
        node.prev = tail
        self.tail = node
        self.length += 1

When adding nodes, we should first judge whether the linked list is empty. In addition, we should set the next attribute for the original tail node, set the prev attribute for the new tail node, and update the tail and length attributes of the linked list.

1. Insert node in linked list:

def insert(self, index, item):
        length = self.length
        if (index<0 and abs(index)>length) or (index>0 and index>=length):
            return False
        if index < 0:
            index = index + length
        if index == 0:
            node = Node(item)
            if self.head != None:
                self.head.prev = node
            else:
                self.tail = node
            node.next = self.head
            self.head = node
            self.length += 1
            return True
        if index == length - 1:
            return self.append(item)


        node1 = self.head
        for i in range(0, index):
            node1 = node1.next
        node2 = node1.next

        node = Node(item)
        node.prex = node1
        node.next = node2
        node1.next = node
        node2.prev = node

        self.length += 1
        return True

When inserting a node, our parameters are subscript index and data item. By default, we insert a new node after the specified subscript.

Here, we also need to consider the head node and tail node.

When inserting, first point the next and prev attributes of the new node to the corresponding node, and then point the next and prev of the front and rear nodes to the new node. At the same time, pay attention to updating the length attribute of the linked list.

Force buckle question 430: flat multi-level two-way linked list

Title:

In the multi-level bidirectional linked list, in addition to the pointer to the next node and the previous node, it also has a sub linked list pointer, which may point to a separate bidirectional linked list. These sub lists may also have one or more of their own sub items, and so on to generate multi-level data structures, as shown in the following example.
Give you the head node at the first level of the list. Please flatten the list so that all nodes appear in the single level double linked list.

Example:

Output is:

python program:

"""
# Definition for a Node.
class Node:
    def __init__(self, val, prev, next, child):
        self.val = val
        self.prev = prev
        self.next = next
        self.child = child
"""
# DFS: depth first search algorithm
class Solution:
    def flatten(self, head: "Node") -> "Node":
        def dfs(node: "Node") -> "Node":
            cur = node
            # Record the last node of the linked list
            last = None

            while cur:
                nxt = cur.next
                # If there are child nodes, the child nodes are processed first
                if cur.child:
                    child_last = dfs(cur.child)
                    
                    nxt = cur.next
                    # Connect node to child:
                    #   Note that you only need to connect 8-11 (the connection of 11-12 has been completed in dfs(cur.child))
                    #   Therefore, there is no need to connect again outside the loop
                    cur.next = cur.child
                    cur.child.prev = cur

                    # If nxt is not empty, connect last with nxt
                    #   The meaning of this paragraph is to connect the last bit of the sub linked list with the next node of the current node
                    if nxt:
                        child_last.next = nxt
                        nxt.prev = child_last

                    # Set child to null
                    cur.child = None
                    last = child_last
                else:
                    last = cur
                cur = nxt

            # The focus of this return value is to return child when looping the dfs process_ Last value;
            # If there is no sub linked list, the return value will not work
            return last

        dfs(head)
        return head