In the last tutorial, we talked about how to draw a rotating colored straight line, in which we have talked about all the elements required for drawing with turtle in detail, that is, configuration, basic graphics, color and animation
In today's article, let's extend the straight line and give a tutorial on how to draw a polygon with spokes with turtle. Its basic shape is as follows:

pentagon

hexagon

360 sided
Does it look cool.
Note that the vertices of the polygon are connected to the center point, that is, there are spokes.
Now please start the performance, taking drawing a Pentagon as an example.
First, we decompose complex problems from the perspective of mathematics and programming.
Pentagons are composed of five concentric triangles with a central angle of 72 °.
The n-sided shape is composed of N concentric triangles with a center angle of 360/N °.
This is the law of mathematics. Primary school Olympiad should have talked about this, manual dog head.
Here, our problem becomes how to draw this triangle, and we want its angle to be variable.
There are two ways to draw triangles:
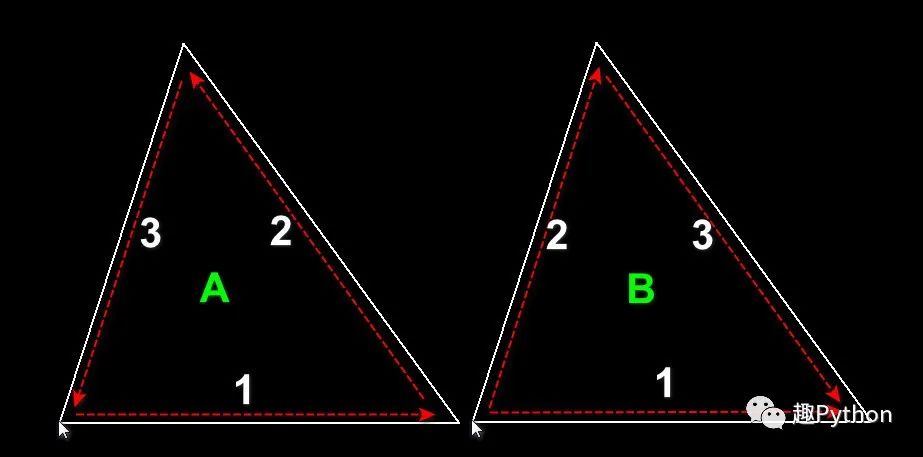
Triangle drawing
The position indicated by the mouse is the center point, and the two edges from the center point are equilateral.
The order of method A is: 1 equilateral - 2 bottom edge - 3 another equilateral
The order of method B is: 1 equilateral - 2 another equilateral - 3 bottom edge
There is no doubt that from the perspective of programming, method B is simpler. Method A needs at least 3-4 mathematical calculations to calculate, and it has to deal with errors. It's too south.
For method B, the programming idea is relatively simple:
- Starting from (0, 0), take the length, and the end point is marked as (x,y)
- Starting from (0, 0), rotate 72 ° (pentagonal) on the basis of 1 and take the length
- Go to point (x,y) and end
We can see that there are few mathematical calculations in this process.

Triangle drawing
Let's get the code out:
length = 400 turtle.goto(0, 0) turtle.pendown() turtle.seth(0) turtle.fd(length) (x,y)=turtle.pos() turtle.penup() turtle.goto(0, 0) turtle.pendown() turtle.seth(72) turtle.fd(length) turtle.goto(x,y) turtle.penup()
In fact, if you get to this step, 80% of the basic knowledge required to draw a polygon is already available.
After drawing the first one, let's draw the second one.
The same code:
turtle.goto(0, 0) turtle.pendown() turtle.seth(72) turtle.fd(length) (x,y)=turtle.pos() turtle.penup() turtle.goto(0, 0) turtle.pendown() turtle.seth(72+72) turtle.fd(length) turtle.goto(x,y) turtle.penup()

Triangle drawing 2
Get here, sharp eyed students must have found something?
The first picture and the second picture are the same except for the different angles. Why don't you rebuild it and wait for the new year??
length = 400
for index in range(5):
turtle.goto(0, 0)
turtle.pendown()
turtle.seth(72*index)
turtle.fd(length)
(x,y)=turtle.pos()
turtle.penup()
turtle.goto(0, 0)
turtle.pendown()
turtle.seth(72*(index+1))
turtle.fd(length)
turtle.goto(x,y)
turtle.penup()

pentagon
Beautiful, a perfect Pentagon.
Let's refactor the code to support N-sided shapes.
def draw_gon(length, line):
angle = 360//line
for index in range(line):
turtle.goto(0, 0)
turtle.pendown()
turtle.seth(angle*index)
turtle.fd(length)
(x,y)=turtle.pos()
turtle.penup()
turtle.goto(0, 0)
turtle.pendown()
turtle.seth(angle*(index+1))
turtle.fd(length)
turtle.goto(x,y)
turtle.penup()
Here, the basic functions are completed.
Here, every time we start painting, we draw to the East. We reconstruct it again, add a starting angle value to it, and lay the groundwork for our later rotation.
def draw_gon(length, start_angle, line):
angle = 360//line
for index in range(line):
turtle.goto(0, 0)
turtle.pendown()
turtle.seth(start_angle + angle*index)
turtle.fd(length)
(x,y)=turtle.pos()
turtle.penup()
turtle.goto(0, 0)
turtle.pendown()
turtle.seth(start_angle+angle*(index+1))
turtle.fd(length)
turtle.goto(x,y)
turtle.penup()

Pentagon_ Angle 10
Finally, give us the beautiful pictures of each polygon:

Octagonal

nonagon

Decagonal

Dodecagonal
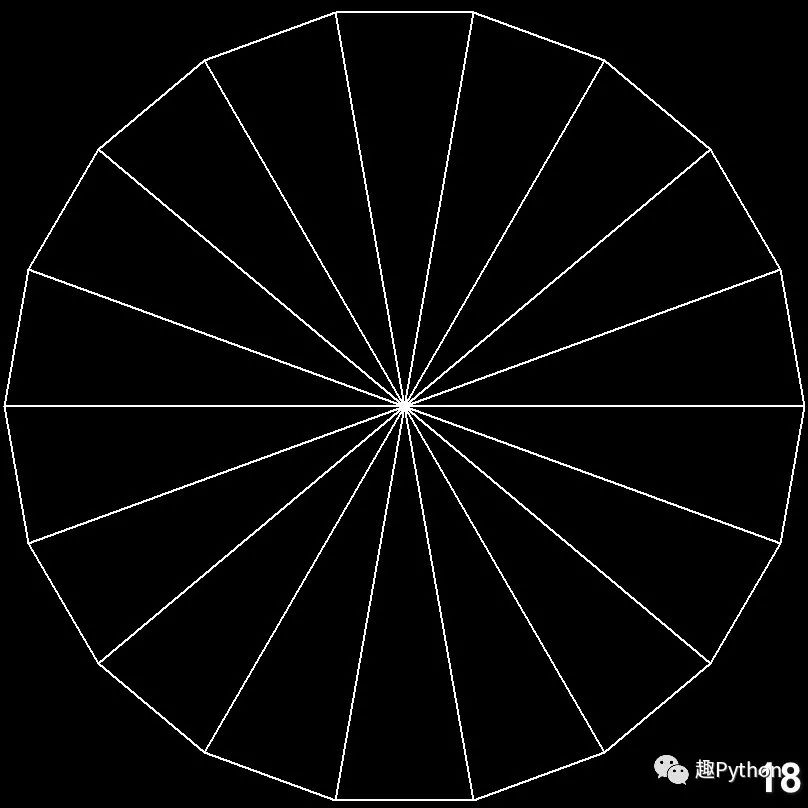
Octagonal
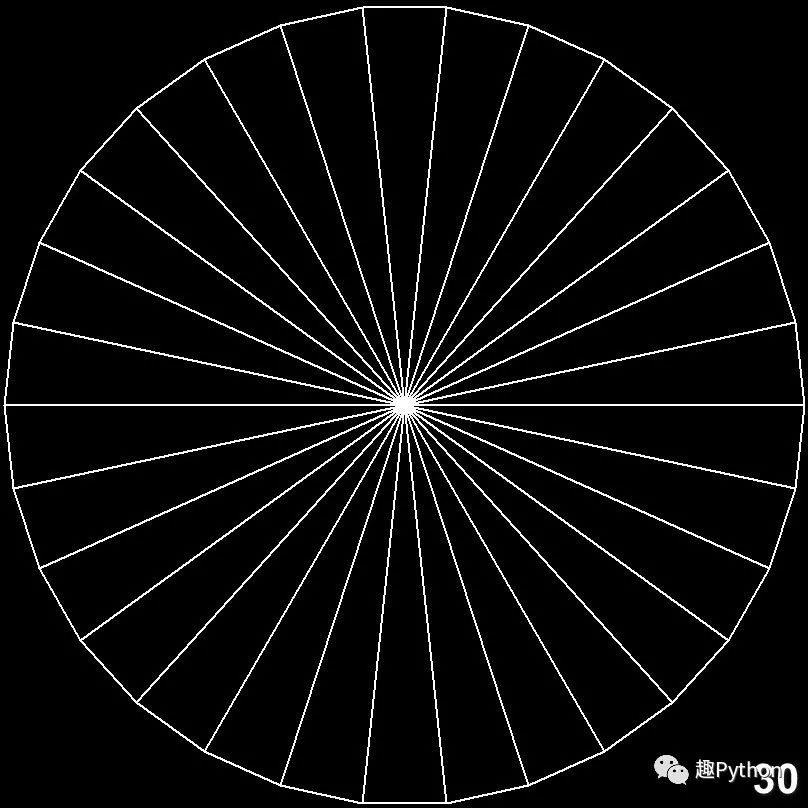
Triangular