1. Algorithmic Concepts

Algorithms: is a calculation process, the way to solve problems.

2. Recursion

2.1. Recursive characteristics

Recursive algorithm is a process that calls its own algorithm directly or indirectly. In computer programming, it often makes the description of the algorithm concise and easy to understand.
The characteristics of recursive algorithms for solving problems:
(1) Recursion refers to calling oneself in a procedure or function.
(2) When using a recursive strategy, there must be a clear end condition for recursion, called a recursive exit.
(3) Recursive algorithm solving is usually very concise, but the efficiency of recursive algorithm solving is low, so it is generally not advocated to use recursive algorithm to design programs.
(4) In the process of recursive calls, the system has opened up a new stack to store the return points and local quantities of each layer. Too many recursions can easily cause stack overflow, etc.
Recursive Requirements
Recursive algorithms generally have three requirements for "repetition":
(1) Each call is reduced in size (usually by half).
(2) There is a close relationship between two adjacent repeats, the previous one being prepared for the latter (usually the previous output being the latter input).
(3) The answer must be given directly without making recursive calls at the smallest scale of the question, so every recursive call is conditional (depending on the size of the direct answer not being reached). An unconditional recursive call will become a dead loop and will not end properly.

2.2. Simple recursive function example:

def recursion(i): #Define function
    print(i)
    If i/2 > 1: #Judge recursion condition, exit
        re = recursion(i/2) #Recursive function itself
        print('return value:', re)
    print('upper recursive value:', i)
    return i #return value

recursion(10)

#Running principle: first run the function parameter 10 to the function, print 10, judge the condition is satisfied, recursive
 #Function parameter value is (10/2)5, print i value 5, etc. when recursive to 1.25, the judgment is not satisfied
 #Foot before printing the upper recursive value, where the recursive value is 1.25, return recursive last
 Layer #with a value of 1.25, exits the last level of recursion, continues one level to exit recursion, and finally returns to the top
 #Recursive value end function.
'''
10
5.0
2.5
1.25
 Upper Recursive Value: 1.25
 Return value: 1.25
 Upper Recursive Value: 2.5
 Return value: 2.5
 Upper Recursive Value: 5.0
 Return value: 5.0
 Upper Recursive Value: 10
'''

Fibonacci series: the sum of the first two numbers is the value of the last (0, 1, 1, 2, 3, 5, 8, 13...)

def foo(arg1,arg2,stop):
    if arg1 == 0:
        print(arg1,arg2)
    arg3 = arg1 + arg2
    print(arg1,arg2,arg3)
    if arg3 < stop:      #Exit recursion when a suite is not satisfied
        foo(arg2,arg3,stop)   #Recursive function, passing arg2,arg3,stop to arg1,arg2,stop

foo(0,1,50)

'''
0 1
0 1 1
1 1 2
1 2 3
2 3 5
3 5 8
5 8 13
8 13 21
13 21 34
21 34 55
'''

Find data using slice recursion:

def twosplit(sourceDate,findData):
    sp = int(len(sourceDate)/2)  #Sequence Length
    if sourceDate[0] == findData:
        print('Find data:',sourceDate[0])
        return 0
    else:
        if findData in sourceDate[:sp]: #Judgement on the left
            print('Data on the left[%s]' %sourceDate[:sp])
            twosplit(sourceDate[:sp],findData)  #Recursive function
        elif findData in sourceDate[sp:]: #Judgement on the right
            print('Data on the right[%s]' %sourceDate[sp:])
            twosplit(sourceDate[sp:], findData)
        else:
            print('No data found')

if __name__ == '__main__':
    data = [1,2,'c',3,4,5,6,7,8,17,26,15,14,13,12,11,'a','b']
    #data = list(range(1000000))
    twosplit(data,'c')

Binary array, 90 degree clockwise data exchange:

a = [[col for col in range(4)] for row in range(4)]
for i in a:print(i)   #Print 2-D Array
print('--------------------')
for lf,rig in enumerate(a):  #Loop Array, Print Array Subscripts and Elements
    for cf in range(lf,len(rig)):  #Loop from subscript array to list length 
        tmp = a[cf][lf]      #Stores elements in list elements
        a[cf][lf] = rig[cf]  
        a[lf][cf] = tmp
    print('+++++++++++++++++')
    for i in a:print(i)

'''
#Another way
for i in range(len(a)):
    ai = [a[i][i] for row in range(4)]
    print(ai)
'''

2.3. Recursion principle

When a function is called, it opens a new stack in which the code in the body of the function is executed.
2.3.1, print() statements before recursion
Code that precedes a function call is executed before the subsequent function call is executed.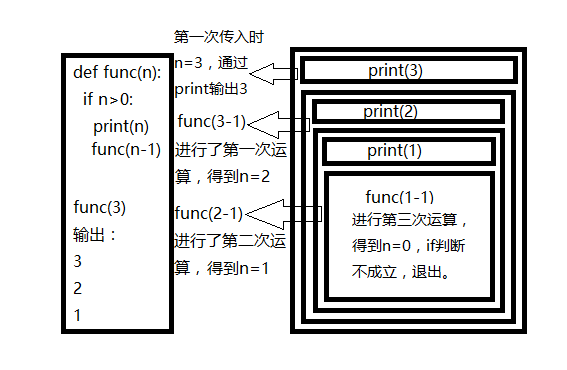

2.3.2, print() statements after recursion
Code that follows a function call waits until all calls to the function have been executed before executing from the inside out.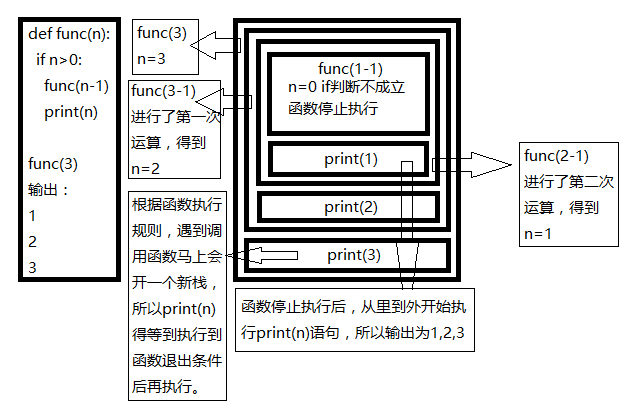

3. Binary Search

To exclude half of the data at a time, the efficiency of the search is very high, but the limitations are relatively large; there must be a sequence table to use binary search.

# 1. Non-recursive algorithm
    def binary_search(lis, nun):
        left = 0
        right = len(lis) - 1
        while left <= right:   #Cyclic condition
            mid = (left + right) // 2   #Gets the middle position, the index of the number (sequence precondition is ordered)
            if num < lis[mid]:  #If the number of queries is smaller than the middle number, go to the left after the dichotomy.
                right = mid - 1   #When you get to the left, you need to change the right boundaries to mid-1
            elif num > lis[mid]:   #If the query number is larger than the middle number, look to the right after the dichotomy
                left = mid + 1    #When you get to the right, you need to change the left boundary to mid+1
            else:
                return mid  #If the query number happens to be an intermediate value, return the value to be indexed
        return -1  #If the loop ends, the left side is larger than the right side, indicating that it was not found

    lis = [11, 32, 51, 21, 42, 9, 5, 6, 7, 8]
    print(lis)
    lis.sort()
    print(lis)
    while 1:
        num = int(input('Enter the number to look for:'))
        res = binary_search(lis, num)
        print(res)
        if res == -1:
            print('Not found!')
        else:
            print('Find it!')

# 2. Recursive algorithm
    def binary_search(lis, left, right, num):
        if left > right: #Recursive End Conditions
            return -1
        mid = (left + right) // 2
        if num < lis[mid]:
            right = mid -1
        elif num > lis[mid]:
            left = mid + 1
        else:
            return mid
        return binary_search(lis, left, right, num)
        #There is a return here because you have to receive a value or return None
        #Back to the last level, if there is no return, then None will be returned
        
    lis = [11, 32, 51, 21, 42, 9, 5, 6, 7, 8]
    print(lis)
    lis.sort()
    print(lis)
    while 1:
        num = int(input('Enter the number to look for:'))
        res = binary_search(lis, 0, len(lis)-1,num)
        print(res)
        if res == -1:
            print('Not found!')
        else:
            print('Find it!')