Introduction of Selective Sorting

Selection sort is a simple and intuitive sorting algorithm. Firstly, the smallest (large) element is found in the unordered sequence and stored at the beginning of the ordered sequence. Then, the smallest (large) element is searched from the remaining unordered elements and placed at the end of the ordered sequence. By analogy, until all elements are sorted.

The main advantage of selective sorting is related to data movement. If an element is in the right final position, it will not be moved. Select sort to swap a pair of elements each time, at least one of them will be moved to its final position, so sorting the list of n elements will be done for a total of n-1 swaps. Among all sorting methods that rely entirely on swapping to move elements, selective sorting is a very good one.

2. Principle of Selective Sorting

1. Find the smallest (large) element in the unordered sequence and store it at the beginning of the ordered sequence
2. Continue to find the smallest (largest) element from the remaining unordered elements
3. Then put it at the end of the sorted sequence. By analogy, until all elements are sorted.

3. Graphics of Selective Sorting

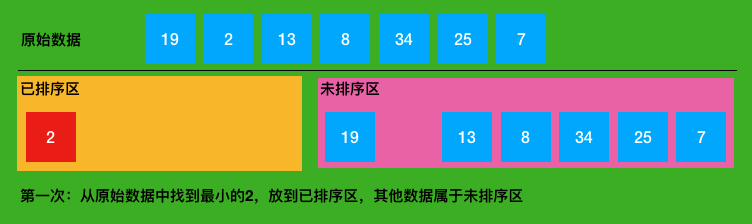
4. Summary of Selection and Sorting

1. With N data, you need to select N-1 times from the unsorted area and put them at the end of the queue in the sorted area.
2. Each time the data selected from the unsorted area is placed at the end of the sorted queue

5. python Code Implementation of Selective Sorting

# Define Selective Sorting Function
def selection_sort(list):
    # Calculate the number of list elements that need to be sorted
    N = len(list)
    # Need N-1 Secondary selection operation
    for i in range(N-1):
        # A small scale for recording minimum values
        minNum_index = i
        # Unordered regions from i+1 tctl eof N Where, belongs to the unordered region, where the minimum value is selected in the unordered region
        for j in  range(i+1,N):
            # Compare size
            if list[minNum_index]>list[j]:
                #exchange
                temp = list[minNum_index]
                list[minNum_index] = list[j]
                list[j] = temp
            
# Create a list
numList = [19,2,13,8,34,25,7]

print("Before sorting:%s"%numList)
# Call Selection Sorting
selection_sort(numList)
print("After sorting:%s"%numList)

The results are as follows:

Before sorting: [19, 2, 13, 8, 34, 25, 7]
After sorting: [2, 7, 8, 13, 19, 25, 34]

6. Implementation of Selective Sorting in C Language Code

Version 1

#include <stdio.h>
//Define Selective Sorting Function
void selection_sort(int array[],int arrayLenght)
{
    // Need N-1 Secondary selection operation
    for (int i=0; i<arrayLenght-1; i++)
    {
        // Subscription of record minimum
        int minNum_index = i;
        // Unordered regions from i+1 tctl eof N Where, belong to the unordered region, and then select the minimum value in the unordered region.
        for (int j = i+1; j<arrayLenght; j++)
        {
            // Compare size
            if (array[minNum_index]>array[j])
            {
                // exchange
                int temp = array[minNum_index];
                array[minNum_index] = array[j];
                array[j] = temp;
            }
        }
    }
}

int main(int argc, const char * argv[]) {
   
    // Selection sort function declaration
    void selection_sort(int array[],int arrayLenght);
    // Create arrays
    int numArray[] = {19,2,13,8,34,25,7};
    // Call Sorting
    selection_sort(numArray, 7);
    // Verification
    for (int i =0; i<7; i++)
    {
        printf("%d ",numArray[i]);
    }

    return 0;
}

The results are as follows:

2 7 8 13 19 25 34

Version 2

#include <stdio.h>
//Define Selective Sorting Function
void selection_sort1(int array[],int arrayLenght)
{
    // Need N-1 Secondary selection operation
    for (int i=0; i<arrayLenght-1; i++)
    {
        // Subscription of record minimum
        int minNum_index = i;
        // Unordered regions from i+1 tctl eof N Where, belong to the unordered region, and then select the minimum value in the unordered region.
        for (int j = i+1; j<arrayLenght; j++)
        {
            // Compare size
            if (array[minNum_index]>array[j])
            {
                minNum_index = j;
            }
        }
        if (minNum_index != i)
        {
            int temp = array[i];
            array[i] = array[minNum_index];
            array[minNum_index] = temp;
            
        }
    }
}

int main(int argc, const char * argv[]) {
   
    // Selection sort function declaration
    void selection_sort1(int array[],int arrayLenght);
    // Create arrays
    int numArray[] = {19,2,13,8,34,25,7};
    // Call Sorting
    selection_sort1(numArray, 7);
    // Verification
    for (int i =0; i<7; i++)
    {
        printf("%d ",numArray[i]);
    }

    return 0;
}

The results are as follows:

2 7 8 13 19 25 34

Seventh, Time Complexity of Selective Sorting

• Optimal time complexity: O(n2)
• Worst-case time complexity: O(n2)

8. Stability of Selective Sorting

Selective sorting is to select the smallest current element for each location, such as the smallest one for the first location, the second smallest one for the remaining elements, and so on, until the n-1 element, the n-th element does not need to be selected, because only one of its largest elements is left. Then, in a single selection, if an element is smaller than the current element, and the small element appears behind an element equal to the current element, then stability is destroyed after exchange. For example, sequence 58529, we know that the first selection of the first element 5 will be exchanged with 2, then the relative order of the two 5 in the original sequence will be destroyed, so the selection sorting is an unstable sorting algorithm.