This tutorial uses Python 3
Reading this article requires some simple physics knowledge.

In the last chapter, we wrote about a small ball bouncing repeatedly under the action of gravity. Now we can simulate the three-body movement.
Three-body motion refers to the motion under the interaction of three celestial bodies with little difference in mass.

I. Define some constants and initialization

from sys import exit
import pygame, math
from pygame.color import *

G     = 900  # Gravitational constant
FPS   = 50   # Frame rate
exact = 50   # Each frame is computed several times, the more times the more accurate, it is dynamic.

pygame.init()  # Initialize pygame
screen = pygame.display.set_mode((640, 480), pygame.DOUBLEBUF, 32)
pygame.display.set_caption("Simulated trisomy")
clock = pygame.time.Clock()
font = pygame.font.SysFont("Arial", 16)

Definition of planetary classes

class Star():
    x , y  = 0, 0  # coordinate
    vx, vy = 0, 0  # Velocity in the X and Y directions
    ax, ay = 0, 0  # Acceleration in the X and Y directions
    m = 0  # quality
    r = 10 # radius

    def __init__(self, x, y, vx, vy, m):
        self.x = x
        self.y = y
        self.vx = vx
        self.vy = vy
        self.m = m

    def set_a(self, other_star):
        '''
        //CALCULATION OF GRAVITY ACCELERATION BETWEEN star AND other_star
        '''
        d_2 = (self.x - other_star.x) ** 2 + (self.y - other_star.y) ** 2
        _x = [-1, 1][self.x < other_star.x]
        _y = [-1, 1][self.y < other_star.y]
        if d_2 != 0:
            a = G * self.m * other_star.m / d_2
        else:
            a = 0
        if self.x != other_star.x:
            ax_ = math.sqrt(a ** 2 / (((self.y - other_star.y) / (self.x - other_star.x)) ** 2 + 1))
            self.ax += ax_ * _x
            self.ay += math.sqrt(a ** 2 - ax_ ** 2) * _y
        else:
            self.ay += a * _y

    def run(self, time):
        '''
        //Location after calculating time time time
        :param time:Time, second 
        :return: 
        '''
        self.ax /= self.m
        self.ay /= self.m
        self.vx += self.ax * time
        self.vy += self.ay * time
        self.x += self.vx * time
        self.y += self.vy * time

3. Setting up Three Planets

star_list = []
dd = 0.00001
star_list.append(Star(200, 300,-30,-math.sqrt(3)*30, 1000))
star_list.append(Star(400, 300,-30, math.sqrt(3)*30, 1000))
star_list.append(Star(300, 300-math.sqrt(3)*100+dd, 60, 0, 1000))

IV. Main Cycle

# Computation of Gravitational Acceleration
def set_a(star_list):
    for i, star in enumerate(star_list):
        star.ax, star.ay = 0, 0
        for j, other_star in enumerate(star_list):
            if i != j:
                star.set_a(other_star)

# Game Main Cycle
while True:
    for event in pygame.event.get():
        if event.type == pygame.QUIT:
            # Exit the program after receiving the exit time
            exit()

    for i in range(exact):
        set_a(star_list)
        for star in star_list:
            star.run(1 / FPS / exact)
    # Draw the background picture on it.
    screen.fill((0, 0, 0))
    max_v = 0
    for star in star_list:
        max_v = max(max_v, math.sqrt(star.vx**2+star.vy**2))
        pygame.draw.circle(screen, (255, 0, 0), (int(star.x), int(star.y)), star.r)
    exact = min(300,max(30,int(max_v)))*5
    screen.blit(font.render("fps: " + str(clock.get_fps()), 1, THECOLORS["white"]), (0,0))
    screen.blit(font.render("exact: " + str(exact), 1, THECOLORS["white"]), (0,15))

    # Refresh screen
    pygame.display.update()
    time_passed = clock.tick(FPS)

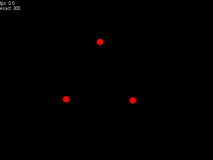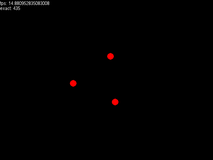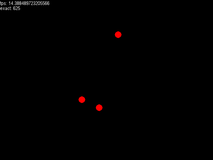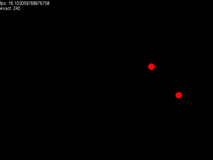
V. Final Effect Chart

A little faster.