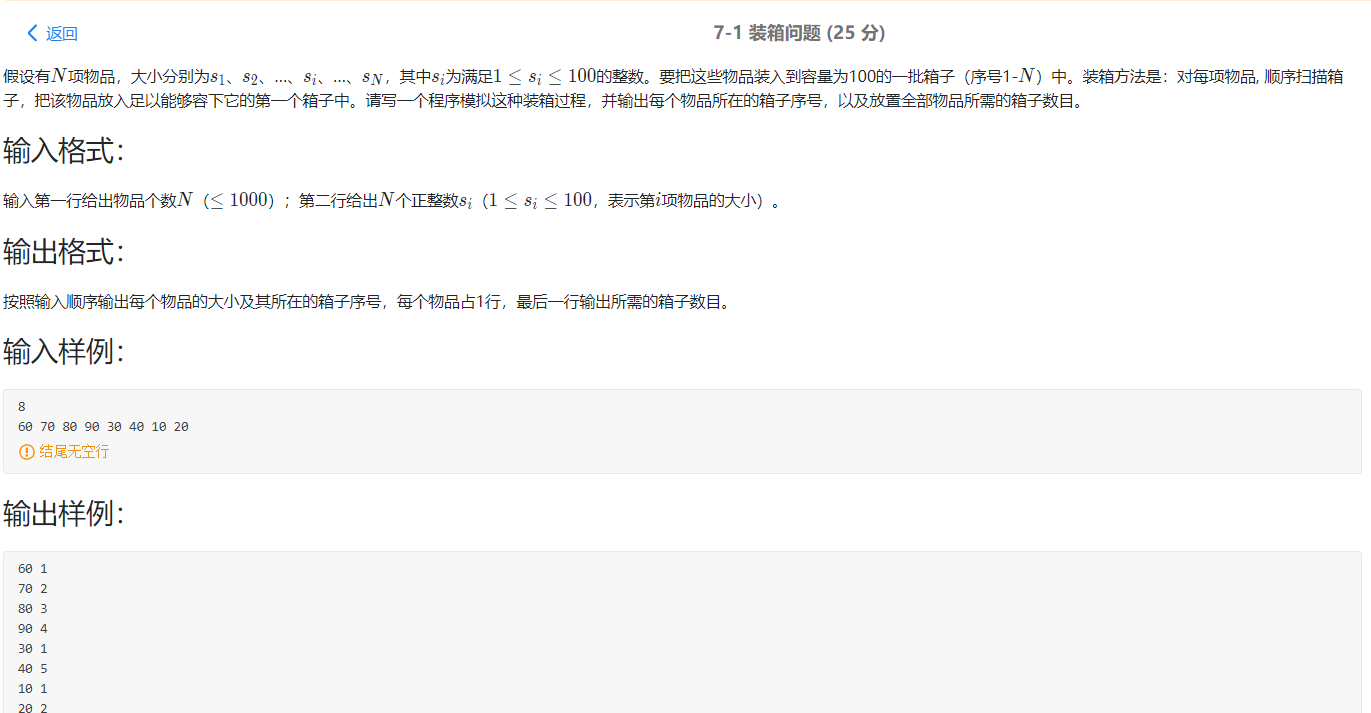
7-1 packing problem
import java.util.Scanner;
public class Program1 {
public static void main(String[] args) {
int N;
Scanner in = new Scanner(System.in);
N = in.nextInt();
int []things = new int[N];
//Up to N boxes
int []box = new int[N];
//Record the maximum number of boxes required
int maxBox = 0;
//Pack each item in sequence
for(int i = 0;i < N;i++){
//Item input
things[i] = in.nextInt();
//Storage simulation
int index = 0;
while (box[index] + things[i] > 100 ){
index++;
}
box[index] += things[i];
System.out.println(things[i] + " " + (index + 1));
if(maxBox < index + 1){
maxBox = index + 1;
}
}
System.out.println(maxBox);
}
}
7-2 moon cake
7-2 moon cakes (25 points)
Moon cake is a traditional food eaten by Chinese people during the Mid Autumn Festival. There are many moon cakes with different flavors in different regions. Given the inventory, total selling price and maximum market demand of all kinds of moon cakes, please calculate the maximum profit you can get.
Note: it is allowed to take out part of the inventory during sales. The example shows that if we have three kinds of moon cakes, the inventory is 180000 tons, 150000 tons and 100000 tons respectively, and the total selling price is 7.5 billion yuan, 7.2 billion yuan and 4.5 billion yuan respectively. If the maximum demand of the market is only 200000 tons, our maximum revenue strategy should be to sell all 150000 tons of the second kind of moon cake and 50000 tons of the third kind of moon cake, and obtain 72 + 45 / 2 = 9.45 billion yuan.
Input format:
Each input contains a test case. Each test case first gives a positive integer no more than 1000, N represents the number of types of moon cakes, and a positive integer no more than 5 (in 10000 tons) D represents the maximum market demand. The next line gives N positive numbers to represent the inventory of each kind of moon cake (in 10000 tons); The last line gives N positive numbers to represent the total selling price of each kind of moon cake (in billion yuan). Numbers are separated by spaces.
Output format:
For each group of test cases, the maximum benefit is output in one line, with 100 million yuan as the unit and accurate to 2 decimal places

This question is super unfriendly to java. It is easy to timeout when using java's own fast queue, and some do not support..... Speechless
Java reference code:
import java.util.Arrays;
import java.util.Comparator;
import java.util.Scanner;
public class Program2 {
/**
* Problem solving idea: select according to the ratio of the number of moon cakes to the selling price. The total profit is the largest if the ratio is the smallest each time
*
*/
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt(); //Types of moon cakes
int D = in.nextInt(); //Total inventory
//The two-dimensional array stores the moon cake inventory and the total selling price respectively
double [][]numValRate = new double[N][2];
for(int i = 0;i < N;i++){
numValRate[i][0] = in.nextDouble();
}
for(int i = 0;i < N;i++){
numValRate[i][1] = in.nextDouble();
}
//Sort from small to large according to the ratio
// The following sorting will timeout on PTA for unknown reasons
//Arrays.sort(numValRate, Comparator.comparingDouble(o -> ((double) o[0] / o[1])));
Arrays.sort(numValRate, new Comparator<double[]>() {
@Override
public int compare(double[] o1, double[] o2) {
if(o1[0] / o1[1] - o2[0] / o2[1] >= 0){
return 1;
}else {
return -1;
}
}
});
double sumVal = 0; //Total revenue
int i = 0;
while (!(D <= 0 || i >= N)){
if(D >= numValRate[i][0]){
D -= numValRate[i][0];
sumVal += numValRate[i][1];
}else {
sumVal += ((double)D / numValRate[i][0]) * numValRate[i][1];
D = 0;
}
i++;
}
System.out.printf("%.2f\n",sumVal);
}
}
C code that can be submitted:
//Greedy moon cake problem
#include <stdio.h>
#include <stdlib.h>
int cmp(const void *_a, const void *_b) {
double *a = (double *) (_a);
double *b = (double *) (_b);
if (a[0] / a[1] - b[0] / b[1] >= 0) {
return 1;
} else {
return -1;
}
}
int main() {
/**
* Problem solving idea: select according to the ratio of the number of moon cakes to the selling price. The total profit is the largest if the ratio is the smallest each time
*
*/
int N; //Types of moon cakes
scanf("%d", &N);
int D; //Total inventory
scanf("%d", &D);
//The two-dimensional array stores the moon cake inventory and the total selling price respectively
double numValRate[N][2];
for (int i = 0; i < N; i++) {
scanf("%lf", &numValRate[i][0]);
}
for (int i = 0; i < N; i++) {
scanf("%lf", &numValRate[i][1]);
}
qsort(numValRate, sizeof(numValRate) / sizeof(numValRate[0]), sizeof(numValRate[0]), cmp);
double sumVal = 0; //Total revenue
int i = 0;
while (!(D <= 0 || i >= N)) {
if (D >= numValRate[i][0]) {
D -= numValRate[i][0];
sumVal += numValRate[i][1];
} else {
sumVal += ((double) D / numValRate[i][0]) * numValRate[i][1];
D = 0;
}
i++;
}
printf("%.2f\n", sumVal);
}
##7-3 vehicle refueling problem (25 points)
Title Source: Wang Xiaodong algorithm design and analysis
A car can travel n kilometers when it is filled with fuel. There are several gas stations on the journey. An effective algorithm is designed to point out which gas stations should stop for refueling, so as to minimize the number of refueling along the way.
Input format:
The first line has two positive integers n and K (k < = 1000), indicating that the car can travel n kilometers after filling up, and there are k gas stations during the journey. The second line has k+1 integers, indicating the distance between the k-th gas station and the k-1 gas station. The 0 gas station indicates the starting place, and the car has been filled up. The k+1 gas station indicates the destination.
Output format:
Output the minimum refueling times. If the destination cannot be reached, output "No Solution!".
import java.util.Scanner;
public class Program3 {
//Greedy algorithm: gasoline refueling problem
//Idea: as long as the remaining oil can reach the next station, don't stop, otherwise stop and refuel
static final String NoSolution = "No Solution!";
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt(); //Total oil tank
int k = in.nextInt(); //Number of destinations
int []pos = new int[k + 1]; //Gas station information
for(int i = 0;i < k + 1;i++){
pos[i] = in.nextInt();
}
int minTime = 0;
int fuelTank = n;
for(int i = 0;i < k + 1;i++){
//Sufficient oil
if(pos[i] <= fuelTank){
fuelTank -= pos[i];
}else if(pos[i] > fuelTank && fuelTank == n){
//Insufficient full tank
minTime = -1;
break;
}else {
//fill the tank up
fuelTank = n;
fuelTank -= pos[i];
minTime++;
}
}
if(minTime >= 0){
System.out.println(minTime);
}else {
System.out.println(NoSolution);
}
}
}
/*
7 7
1 2 3 4 5 1 6 6
*/
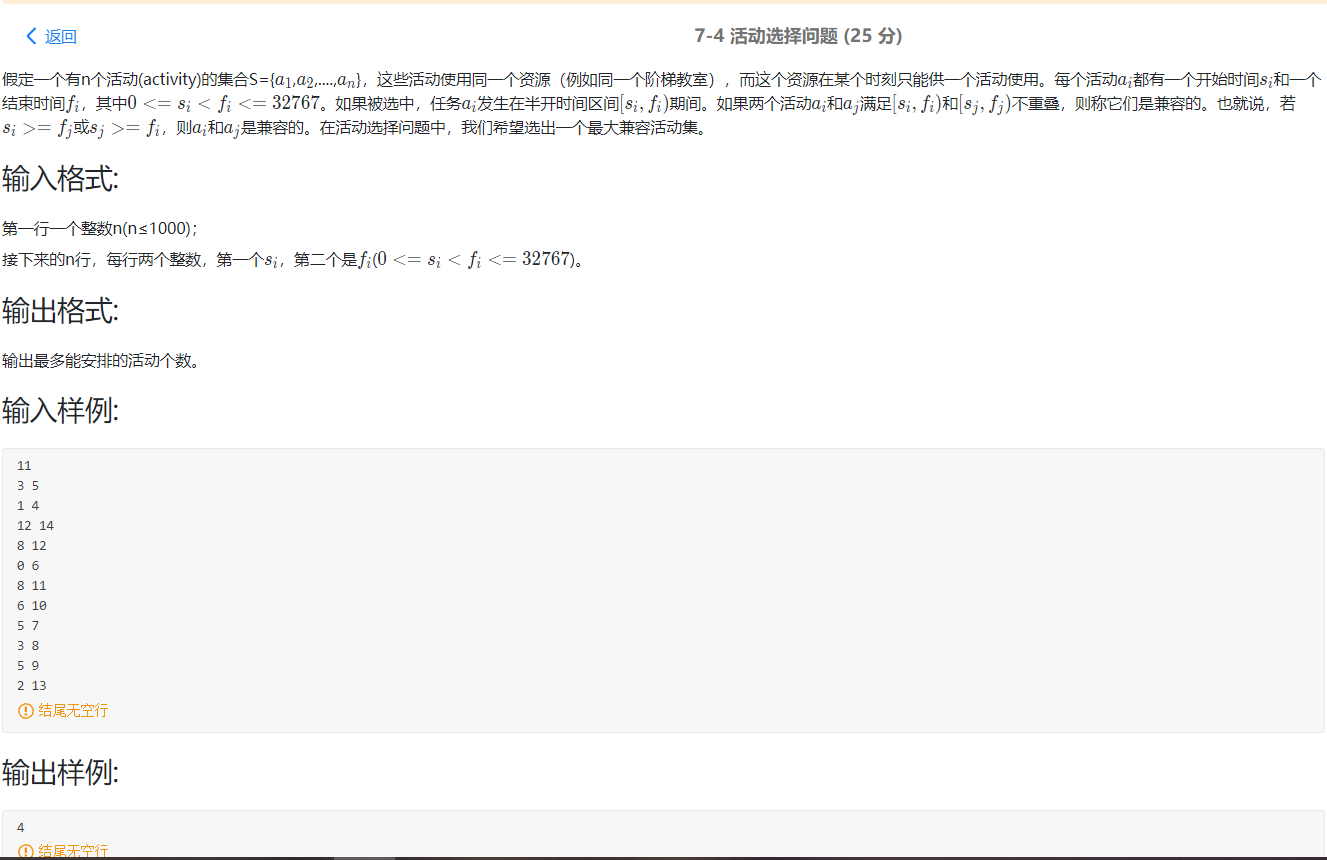
7-4 activity selection
import java.util.Arrays;
import java.util.Comparator;
import java.util.Scanner;
public class Program4 {
//Greed: getting choice
//Idea: select according to the fastest end time of the activity, and the start time is the end time of the previous activity
//The initial start time is 0
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int [][]active = new int[n][2];
for(int i = 0;i < n;i++){
active[i][0] = in.nextInt();
active[i][1] = in.nextInt();
}
//Sort: sort according to the fastest end time, from small to large
Arrays.sort(active, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[1] - o2[1];
}
});
int times = 0; //Maximum number of activities
int startTime = 0;
int index = 0;
while (index < n){
if(startTime <= active[index][0]){
times++;
startTime = active[index][1];
}
index++;
}
System.out.println(times);
}
}
/*
11
3 5
1 4
12 14
8 12
0 6
8 11
6 10
5 7
3 8
5 9
2 13
*/