Priority queues no longer follow the principle of first in, first out. They are divided into two situations:

1. The largest priority queue, regardless of the order of entry, is the current largest element priority out of the queue;

2. The minimum priority queue, regardless of the order of entry, is the current minimum element priority out of the queue;

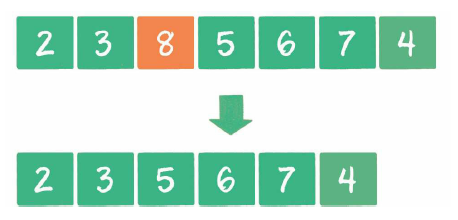
Implementation of priority queue:

Characteristics of binary reactor:

1. The maximum heap top is the largest element in the whole heap;

2. The top of the smallest heap is the smallest element in the whole heap.

Therefore, the maximum priority queue can be realized by using the maximum heap. Each queue entry is the insertion operation of the heap, and the queue exit is the deletion of the top node of the heap. Entering the queue is to put the value at the end of the queue and then float up; leaving the queue is to delete the heap top element, take the last value of the queue and put it on the heap top, and then sink down.

The time complexity of up sink and down float is O(logn).

Code implementation (binary heap implementation priority queue):

using System;
using System.Collections.Generic;

namespace CSharpTest01
{
    class PriorityQueue
    {
        private int[] array;
        private int size;
        public PriorityQueue()
        {
            // Initial length 32
            array = new int[32];
        }
        /// <summary>
        //Team entry
        /// </summary>
        public void EnQueue(int key)
        {
            // Queue length out of range, expanding
            if (size >= array.Length)
            {
                Resize();
            }
            array[size++] = key;
            UpAdjust();
        }
        public int DeQueue()
        {
            if (size <= 0)
            {
                Console.WriteLine("the queue is empty!");
                return -1;
            }
            // Get top element
            int head = array[0];
            // Move the last element to the top of the heap
            array[0] = array[--size];
            DownAdjust();
            return head;
        }
        /// <summary>
        ///Upward adjustment
        /// </summary>
        private void UpAdjust()
        {
            int childIndex = size - 1;
            int parentIndex = (childIndex - 1) / 2;
            // temp saves the inserted leaf node value for the final assignment
            int temp = array[childIndex];
            while (childIndex > 0 && temp > array[parentIndex])
            {
                // One way assignment without real exchange
                array[childIndex] = array[parentIndex];
                childIndex = parentIndex;
                parentIndex = parentIndex / 2;
            }
            array[childIndex] = temp;
        }
        /// <summary>
        ///Sinking adjustment
        /// </summary>
        public void DownAdjust()
        {
            // temp saves the value of the parent node for the final assignment
            int parentIndex = 0;
            int temp = array[parentIndex];
            int childIndex = 1;
            while (childIndex < size)
            {
                // If there is a right child and the right child is greater than the left child, locate the right child
                if (childIndex + 1 < size && array[childIndex + 1] > array[childIndex])
                {
                    childIndex++;
                }
                // If the parent node is greater than the value of any child, directly jump out
                if (temp >= array[childIndex])
                {
                    break;
                }
                array[parentIndex] = array[childIndex];
                parentIndex = childIndex;
                childIndex = 2 * childIndex + 1;
            }
            array[parentIndex] = temp;
        }
        /// <summary>
        ///Queue expansion
        /// </summary>
        private void Resize()
        {
            // Double queue capacity
            int newSize = this.size * 2;
            int[] newArray = new int[newSize];
            Array.Copy(this.array, 0, newArray, 0, this.size);
            this.array = newArray;
        }
    }

    class Program
    {
        static void Main(string[] args)
        {
            PriorityQueue priorityQueue = new PriorityQueue();
            priorityQueue.EnQueue(3);
            priorityQueue.EnQueue(5);
            priorityQueue.EnQueue(10);
            priorityQueue.EnQueue(2);
            priorityQueue.EnQueue(7);
            Console.WriteLine(priorityQueue.DeQueue());
            Console.WriteLine(priorityQueue.DeQueue());
            Console.ReadLine();
        }
    }
}