Referring to ALS, we believe that everyone should not feel strange (not unfamiliar why you click in [cover your face]), it is a kind of collaborative filtering, and is integrated into Spark's MLIB library. This article explains the basic principles of ALS, and hand-in-hand, shoulder-to-shoulder with you to implement this algorithm.

1. Principle chapter

Let's talk about ALS in human language rather than in large mathematical formulas.

1.1 Have you ever heard of recommendation algorithms?

If I were the CEO of Douban, many users of Douban would rate movies on Douban Movies. So based on this rating data, are we likely to know which movies these users like or hate besides the ones they overrated? This is a typical recommendation problem. The algorithm to solve this kind of problem is called recommendation algorithm.

1.2 What is collaborative filtering

Collaborative Filtering (CF) is the full name of collaborative filtering in English. Note that this is not a game! From the literal analysis, synergy is to find common ground, and filtering is to screen out high-quality content.

1.3 Classification of Collaborative Filtering

Generally speaking, collaborative filtering recommendation can be divided into three types:

1. Based on user-based collaborative filtering, users B, C, D., which are similar to user A, are found by calculating the similarity between users and users, and then recommend these users'favorite content to A.
2. Based on item-based collaborative filtering, 2, 3, 4 items similar to Item 1 are found by calculating the similarity of items and items, and then these items are recommended to users who have seen item 1.
3. Model-based collaborative filtering. Mainstream methods can be divided into: matrix decomposition, Association algorithm, clustering algorithm, classification algorithm, regression algorithm, neural network.

1.4 Matrix Decomposition

Matrix decomposition (factorization) is to decompose a matrix into the product of several matrices. For example, Douban movies have m users and N movies. Then the user's evaluation of the movie can form a matrix R of M rows n columns. We can find a matrix U of M rows k columns and a matrix I of k rows n columns, and get the matrix R through U* I.

1.5 ALS

If we want to achieve model-based collaborative filtering through matrix decomposition, ALS is a good choice. Its full name is Alternating Least Square, which is translated into Alternating Least Square. Assuming that the user is a, the item is b, and the score matrix is R(m, n), it can be decomposed into the user matrix U(k, m) and the item matrix I(k, n), where m, N and K represent the dimensions of the matrix. Low-energy early warning of mathematical formulas in the front section:

According to the definition of matrix decomposition, there are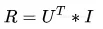

Using MSE as loss function, in order to simplify, the constant on the left side of the additive sign is changed to -1/2.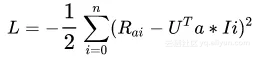

1. Find the first order partial derivative of U_a for the loss function.
   
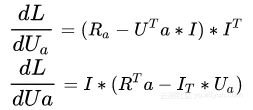
2. Let the first order partial derivative be equal to 0
   
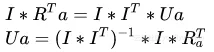
3. The same is true.
   

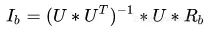
1.6 Solving User Matrix U and Item Matrix I

Matrix R is known. We randomly generate user matrix U.

1. Using Formulas 5, R and U in 1.5 to Find I
2. Using Formulas 6, R and I in 1.5 to Find U

So step 1 and step 2 are executed alternately until the algorithm converges or the number of iterations exceeds the maximum limit. Finally, we use RMSE to evaluate the model.

1. Realization chapter

I have realized ALS algorithm with Python, the simplest programming language in the whole universe. It does not rely on any third-party libraries and is easy to learn and use. For a brief explanation of the implementation process, please refer to the code on my github for more detailed comments.

Note: The Matrix class used in the code is a matrix class I wrote. It can take out the rows or columns of the matrix and calculate the multiplication, transposition and inverse of the matrix.

2.1 Creating ALS Classes

Initialization stores the corresponding relationship between user ID, item ID, user ID and user matrix column number, item ID and item matrix column number, which items the user has seen, Shape of rating matrix and RMSE.

class ALS(object):
    def __init__(self):
        self.user_ids = None
        self.item_ids = None
        self.user_ids_dict = None
        self.item_ids_dict = None
        self.user_matrix = None
        self.item_matrix = None
        self.user_items = None
        self.shape = None
        self.rmse = None

2.2 Data Preprocessing

The training data were processed to obtain the corresponding relationship between user ID, item ID, user ID and user matrix column number, item ID and item matrix column number, Shape of score matrix, score matrix and conversion of score matrix.

def _process_data(self, X):
    self.user_ids = tuple((set(map(lambda x: x[0], X))))
    self.user_ids_dict = dict(map(lambda x: x[::-1],
                                    enumerate(self.user_ids)))

    self.item_ids = tuple((set(map(lambda x: x[1], X))))
    self.item_ids_dict = dict(map(lambda x: x[::-1],
                                    enumerate(self.item_ids)))

    self.shape = (len(self.user_ids), len(self.item_ids))

    ratings = defaultdict(lambda: defaultdict(int))
    ratings_T = defaultdict(lambda: defaultdict(int))
    for row in X:
        user_id, item_id, rating = row
        ratings[user_id][item_id] = rating
        ratings_T[item_id][user_id] = rating

    err_msg = "Length of user_ids %d and ratings %d not match!" % (
        len(self.user_ids), len(ratings))
    assert len(self.user_ids) == len(ratings), err_msg

    err_msg = "Length of item_ids %d and ratings_T %d not match!" % (
        len(self.item_ids), len(ratings_T))
    assert len(self.item_ids) == len(ratings_T), err_msg
    return ratings, ratings_T

2.3 User Matrix Multiplied by Score Matrix

Matrix multiplication of dense matrix and sparse matrix is realized, and the product of user matrix and score matrix is obtained.

def _users_mul_ratings(self, users, ratings_T):

    def f(users_row, item_id):
        user_ids = iter(ratings_T[item_id].keys())
        scores = iter(ratings_T[item_id].values())
        col_nos = map(lambda x: self.user_ids_dict[x], user_ids)
        _users_row = map(lambda x: users_row[x], col_nos)
        return sum(a * b for a, b in zip(_users_row, scores))

    ret = [[f(users_row, item_id) for item_id in self.item_ids]
            for users_row in users.data]
    return Matrix(ret)

2.4 Item Matrix Multiplied by Scoring Matrix

Matrix multiplication of dense matrix and sparse matrix is realized, and product of item matrix and score matrix is obtained.

def _items_mul_ratings(self, items, ratings):

    def f(items_row, user_id):
        item_ids = iter(ratings[user_id].keys())
        scores = iter(ratings[user_id].values())
        col_nos = map(lambda x: self.item_ids_dict[x], item_ids)
        _items_row = map(lambda x: items_row[x], col_nos)
        return sum(a * b for a, b in zip(_items_row, scores))

    ret = [[f(items_row, user_id) for user_id in self.user_ids]
            for items_row in items.data]
    return Matrix(ret)

2.5 Generating Random Matrix

def _gen_random_matrix(self, n_rows, n_colums):
    data = [[random() for _ in range(n_colums)] for _ in range(n_rows)]
    return Matrix(data)

2.6 Computing RMSE

def _get_rmse(self, ratings):
        m, n = self.shape
        mse = 0.0
        n_elements = sum(map(len, ratings.values()))
        for i in range(m):
            for j in range(n):
                user_id = self.user_ids[i]
                item_id = self.item_ids[j]
                rating = ratings[user_id][item_id]
                if rating > 0:
                    user_row = self.user_matrix.col(i).transpose
                    item_col = self.item_matrix.col(j)
                    rating_hat = user_row.mat_mul(item_col).data[0][0]
                    square_error = (rating - rating_hat) ** 2
                    mse += square_error / n_elements
        return mse ** 0.5

2.7 Training Model

Data preprocessing

Validity check of Variable k

Generating Random Matrix U

Alternately calculate matrix U and matrix I and print RMSE information until the number of iterations reaches max_iter

Save the final RMSE

def fit(self, X, k, max_iter=10):
    ratings, ratings_T = self._process_data(X)
    self.user_items = {k: set(v.keys()) for k, v in ratings.items()}
    m, n = self.shape

    error_msg = "Parameter k must be less than the rank of original matrix"
    assert k < min(m, n), error_msg

    self.user_matrix = self._gen_random_matrix(k, m)

    for i in range(max_iter):
        if i % 2:
            items = self.item_matrix
            self.user_matrix = self._items_mul_ratings(
                items.mat_mul(items.transpose).inverse.mat_mul(items),
                ratings
            )
        else:
            users = self.user_matrix
            self.item_matrix = self._users_mul_ratings(
                users.mat_mul(users.transpose).inverse.mat_mul(users),
                ratings_T
            )
        rmse = self._get_rmse(ratings)
        print("Iterations: %d, RMSE: %.6f" % (i + 1, rmse))

    self.rmse = rmse

2.8 Predict a User

Predict what a user is interested in and exclude what the user has seen. Then, according to the score of interest, the first n_items are extracted.

def _predict(self, user_id, n_items):
    users_col = self.user_matrix.col(self.user_ids_dict[user_id])
    users_col = users_col.transpose

    items_col = enumerate(users_col.mat_mul(self.item_matrix).data[0])
    items_scores = map(lambda x: (self.item_ids[x[0]], x[1]), items_col)
    viewed_items = self.user_items[user_id]
    items_scores = filter(lambda x: x[0] not in viewed_items, items_scores)

    return sorted(items_scores, key=lambda x: x[1], reverse=True)[:n_items]

2.9 Predict Multiple Users

Loop call 2.8 to predict content of interest to multiple users.

def predict(self, user_ids, n_items=10):
    return [self._predict(user_id, n_items) for user_id in user_ids]

3. Effectiveness evaluation

3.1 main function

Movie scoring data sets were used to train the model and to count RMSE.

@run_time
def main():
    print("Tesing the accuracy of ALS...")

    X = load_movie_ratings()

    model = ALS()
    model.fit(X, k=3, max_iter=5)
    print()

    print("Showing the predictions of users...")

    user_ids = range(1, 5)
    predictions = model.predict(user_ids, n_items=2)
    for user_id, prediction in zip(user_ids, predictions):
        _prediction = [format_prediction(item_id, score)
                       for item_id, score in prediction]
        print("User id:%d recommedation: %s" % (user_id, _prediction))

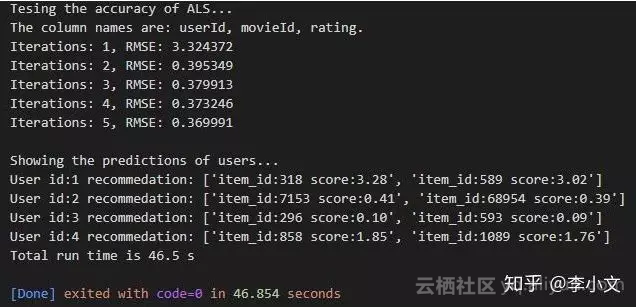
3.2 Effect Show

Set k=3, iterate 5 times, and show the recommended content of the first four users. Finally, RMSE is 0.370, running time is 46.5 seconds, and the effect is good.~

3.3 Tool Functions

I have customized some tool functions, which can be viewed on github:

https://github.com/tushushu/imylu/tree/master/imylu/utils

1. run_time - Test function run time
2. load_movie_ratings - Load movie rating data

summary

Principle of ALS: laying eggs and laying hens

ALS Implementation: Basically Matrix Multiplication

The original release date is 2019-1-2.
Author: Li Xiaowen
This article is from Yunqi Community Partners“ Python enthusiast community For information, you can pay attention to "python_shequ" Wechat Public Number