Clustering refers to the classification of data according to the characteristics of the data itself, which does not require manual standards. It is a kind of unsupervised learning.The k-means algorithm is one of the simplest clustering algorithms.

The k-means algorithm divides n data objects into K clusters to make the obtained clusters satisfy: objects in the same cluster have higher similarity; objects in different clusters have smaller similarity.Cluster similarity is calculated by using the mean of the objects in each cluster to obtain a "center object" (gravitational center).

Based on this assumption, let's export the objective function that k-means will optimize again: let's say we have N data points that need to be divided into K cluster s, and what k-means will do is to minimize this objective function

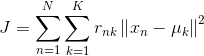
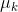Is the k th cluster center,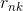1 when the nth data belongs to class k, otherwise 0.

The process is as follows:

1. Select k objects from n data objects as initial cluster centers at first; for the remaining objects, assign them to the most similar cluster according to their similarity (distance) with those cluster centers.

2. Then calculate the cluster center of each new cluster (for all objects in the cluster) mean value ); Repeat this process until the standard measure function begins to converge.

Generally, the mean square deviation is used as the standard measure function. k clusters have the following characteristics: the clusters themselves are as compact as possible, and the clusters are as separate as possible.

Each update of the cluster center reduces the objective function, so the iteration final J will reach a minimum, which is not guaranteed to be the global minimum.k-means are very sensitive to noise.

c++ implementation:

class ClusterMethod
{
private:
	double **mpSample;//input
	double **mpCenters;//Storage Cluster Centers
	double **pDistances;//Distance Matrix
	int mSampleNum;//Number of samples
	int mClusterNum;//Number of Clusters
	int mFeatureNum;//Number of features per sample
	int *ClusterResult;//Clustering results
	int MaxIterationTimes;//Maximum number of iterations

public:
	void GetClusterd(vector<std::vector<std::vector<double> > >&v, double** feateres, int ClusterNum, int SampleNum, int FeatureNum);//External Interface


private:
	void Initialize(double** feateres, int ClusterNum, int SampleNum, int FeatureNum);//Class Initialization
	void k_means(vector<vector<vector<double> > >&v);//Algorithm entry
	void k_means_Initialize();//Membership Matrix Initialization
	void k_means_Calculate(vector<vector<vector<double> > >&v);//Cluster calculation
};

Intra-class function implementation:

//param@v saves the classification result v[i][j][k] to represent the kth feature of the jth data in class I (starting from 0)
//param@feateres Input data feateres[i][j] represents the jth feature of the ith data (i, J starts from 0)
//Number of param@ClusterNum categories
//Number of param@SampleNum data
//param@FeatureNum Data Feature Number
void ClusterMethod::GetClusterd(vector<std::vector<std::vector<double> > >&v, double** feateres, int ClusterNum, int SampleNum, int FeatureNum)
{
	Initialize(feateres, ClusterNum, SampleNum, FeatureNum);
	k_means(v);
}


//Intra-class data initialization
void ClusterMethod::Initialize(double** feateres, int ClusterNum, int SampleNum, int FeatureNum)
{
	mpSample = feateres;
	mFeatureNum = FeatureNum;
	mSampleNum = SampleNum;
	mClusterNum = ClusterNum;
	MaxIterationTimes = 50;

	mpCenters = new double*[mClusterNum];
	for (int i = 0; i < mClusterNum; ++i)
	{
		mpCenters[i] = new double[mFeatureNum];
	}

	pDistances = new double*[mSampleNum];
	for (int i = 0; i < mSampleNum; ++i)
	{
		pDistances[i] = new double[mClusterNum];
	}

	ClusterResult = new int[mSampleNum];
}


//Algorithm entry
void ClusterMethod::k_means(vector<vector<vector<double> > >&v)
{
	k_means_Initialize();
	k_means_Calculate(v);
}


//Initialize Cluster Center
void ClusterMethod::k_means_Initialize()
{
	for (int i = 0; i < mClusterNum; ++i)
	{
		//mpCenters[i] = mpSample[i];

		for (int k = 0; k < mFeatureNum; ++k)
		{
			mpCenters[i][k] = mpSample[i][k];
		}
	}
}

Initializing the cluster centers above is to make the first I (i is the number of cluster centers) points of the data iCluster centers.(Note that mpCenters[i] = mpSample[i] must not be used for initialization; they are pointers.)

You can also randomly select i data as the cluster center, so that the same data may run differently multiple times.Because k-means results do not necessarily reach the global minimum, the easiest solution is to run multiple times (in this case, the entire function runs repeatedly, different from the number of iterations in clustering) to get the clustering result at the minimum of the objective function.If the cluster center is initialized with the first i data each time, as before, multiple runs will not solve the local minimum point problem.

Clustering and updating cluster centers are implemented as follows:

//Clustering process
void ClusterMethod::k_means_Calculate(vector<vector<vector<double> > >&v)
{

	double J = DBL_MAX;//objective function
	int time = MaxIterationTimes;

	while (time)

	{
		double now_J = 0;//Target function after last update of distance Center
		--time;
                
                //Distance Initialization
		for (int i = 0; i < mSampleNum; ++i)
		{
			for (int j = 0; j < mClusterNum; ++j)
			{
				pDistances[i][j] = 0;

			}
		}
                //Calculate Euclidean Distance
		for (int i = 0; i < mSampleNum; ++i)
		{
			for (int j = 0; j < mClusterNum; ++j)
			{
				for (int k = 0; k < mFeatureNum; ++k)
				{
					pDistances[i][j] += abs(pow(mpSample[i][k], 2) - pow(mpCenters[j][k], 2));
				}
				now_J += pDistances[i][j];
			}
		}
	
		if (J - now_J < 0.01)//The objective function stops changing and ends the loop
		{	
			break;
		}
		J = now_J;

                //a Stores temporary classification results
		vector<vector<vector<double> > > a(mClusterNum);
		for (int i = 0; i < mSampleNum; ++i)
		{
			
			double min = DBL_MAX;
			for (int j = 0; j < mClusterNum; ++j)
			{
				if (pDistances[i][j] < min)
				{
					min = pDistances[i][j];
					ClusterResult[i] = j;
				}
			}

			vector<double> vec(mFeatureNum);
			for (int k = 0; k < mFeatureNum; ++k)
			{
				vec[k] = mpSample[i][k];
			}
			a[ClusterResult[i]].push_back(vec);
		//	v[ClusterResult[i]].push_back(vec); this cannot be done here because v has no initialization size
		}
		v = a;

		//Calculating New Cluster Centers
		for (int j = 0; j < mClusterNum; ++j)
		{
			for (int k = 0; k < mFeatureNum; ++k)
			{

				mpCenters[j][k] = 0;
			}
		}


		for (int j = 0; j < mClusterNum; ++j)
		{
			for (int k = 0; k < mFeatureNum; ++k)
			{
				for (int s = 0; s < v[j].size(); ++s)
				{
					mpCenters[j][k] += v[j][s][k];
				}
				if (v[j].size() != 0)
				{
					mpCenters[j][k] /= v[j].size();
				}
			}
		}
	}

        //Output Cluster Center
	for (int j = 0; j < mClusterNum; ++j)
	{
		for (int k = 0; k < mFeatureNum; ++k)
		{
			cout << mpCenters[j][k] << " ";
		}
		cout << endl;
	}
}

Generate Random Data Function:

//Number of param@datanum data
//param@featurenum number of features per data
double** createdata(int datanum, int featurenum)
{
	srand((int)time(0));
	double** data = new  double*[datanum];
	for (int i = 0; i < datanum; ++i)
	{
		data[i] = new double[featurenum];
	}
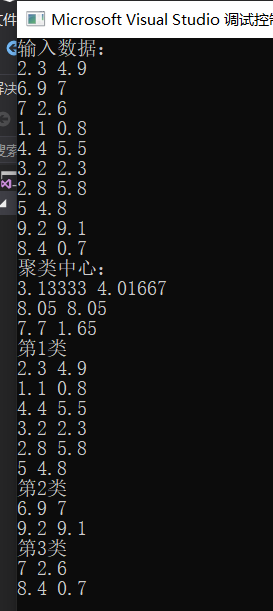
	cout << "Input data:" << endl;
	for (int i = 0; i < datanum ; ++i)
	{
		for (int j = 0; j < featurenum; ++j)
		{
			data[i][j] = ((int)rand() % 30) / 10.0;
			cout << data[i][j] << " ";
		}
		cout << endl;
	}

	return data;
}

Main function:

int main()
{
	vector<std::vector<std::vector<double> > >v;
	double** data = createdata(10, 2);
	ClusterMethod a;
	a.GetClusterd(v, data, 3, 10, 2);
	for (int i = 0; i < v.size(); ++i)
	{
		cout << "No." << i+1 << "class" << endl;
		for (int j = 0; j < v[i].size(); ++j)
		{
			for (int k = 0; k < v[i][j].size(); ++k)
			{
				cout << v[i][j][k] << " ";
			}
			cout << endl;
		}	
	}
}

The results are as follows: