PriorityBlockingQueue is an unbounded array based priority blocking queue. The default length of the array is 11. Although the length of the array is specified, it can be expanded indefinitely until the resources are exhausted. Each time out of the queue, the element with the highest or lowest priority is returned. By default, elements are sorted in natural ascending order. Of course, we can also specify Comparator through constructor to sort elements. It should be noted that PriorityBlockingQueue cannot guarantee the order of elements with the same priority.
Priority queue: each element in the queue has a priority. When leaving the queue, the highest priority is first out.

It is worth noting that although PriorityBlockingQueue is called priority queue, it does not mean that elements will be sorted according to the sorting rules as soon as they enter the queue, but only the queue order transferred out by calling take, poll method or drawto is sorted by the priority queue. Therefore, the element order of iterator iterations returned by calling iterator() and splittable iterator() methods is not sorted. If you need to traverse in order, you can sort through the Arrays.sort(pq.toArray()) method. Note that the peek method always gets and does not delete the first element, so multiple calls to peek return the same value.
Application scenario
In e-commerce rush buying activities, users with high membership level have priority to rush to buy goods
Banks handle business, vip customers jump in line
1 /** 2 * Default array capacity. The default array capacity. 3 */ 4 private static final int DEFAULT_INITIAL_CAPACITY = 11; 5 6 /** 7 * The maximum size of array to allocate. The maximum size of the array to allocate. 8 * Some VMs reserve some header words in an array. Some VMS keep some header information in the array 9 * Attempts to allocate larger arrays may result in 10 * OutOfMemoryError: Requested array size exceeds VM limit 11 Attempting to allocate a larger array may result in OutOfMemoryError: the requested array size exceeds the VM limit 12 */ 13 private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8; 14 15 /** 16 * Priority queue represented as a balanced binary heap: the two 17 * children of queue[n] are queue[2*n+1] and queue[2*(n+1)]. The 18 * priority queue is ordered by comparator, or by the elements' 19 * natural ordering, if comparator is null: For each node n in the 20 * heap and each descendant d of n, n <= d. The element with the 21 lowest value is in queue[0], assuming the queue is nonempty. 22 23 The priority queue is represented as a balanced binary heap: the two sub queues of queue[n] are queue[2*n+1] and queue[2*(n+1)]. 24 25 The priority queue is sorted by the comparator or the natural order of elements. If the comparator is null: for each node n in the heap and each child node D of N, n < = D. Assuming that the queue is not empty, the value in queue[0] is the smallest. 26 27 */ 28 private transient Object[] queue; 29 30 /** 31 * The number of elements in the priority queue. Number of elements in the priority queue. 32 */ 33 private transient int size; 34 35 /** 36 * The comparator, or null if priority queue uses elements' 37 * natural ordering. Comparator, null if the priority queue uses the natural order of elements. 38 */ 39 private transient Comparator<? super E> comparator; 40 41 /** 42 * Lock used for all public operations Locks for all public operations 43 */ 44 private final ReentrantLock lock; 45 46 /** 47 * Condition for blocking when empty 48 */ 49 private final Condition notEmpty; 50 51 /** 52 * Spinlock for allocation, acquired via CAS. Spin lock for allocation, obtained through CAS. 53 */ 54 private transient volatile int allocationSpinLock; 55 56 /** 57 * A plain PriorityQueue used only for serialization, 58 * to maintain compatibility with previous versions 59 * of this class. Non-null only during serialization/deserialization. 60 An ordinary PriorityQueue, which is only used for serialization to maintain compatibility with previous versions of the class. 61 Non null only during serialization / deserialization. 62 */ 63 private PriorityQueue<E> q;
The member properties are very simple and clear at a glance. In theory, the maximum capacity of the queue can be up to Integer.MAX_VALUE - 8 (minus 8 is because some JVM implementations will save object header information in the array). The Object[] queue is actually used to store queue elements. This is similar to ArrayBlockingQueue. It uses an array to store queue elements, but PriorityBlockingQueue is not a first in first out queue. In fact, it uses a balanced binary heap, How to understand this? Although the array is a one-dimensional data structure, its storage order is stored in the array from top to bottom and from left to right according to the binary tree. The balanced binary tree has a root node, namely queue[0], which is also the smallest element. Under the root node, there are two child nodes, the left child node corresponds to queue[1], the right child node corresponds to queue[2], and then the left and right child nodes have their own two child nodes. By analogy, the binary tree corresponds to the array. Each node in the balanced binary heap is less than or equal to its two child nodes.
Then comes the construction method. PriorityBlockingQueue has three construction methods, which can specify the initial capacity, the unified Comparator instance and the initial collection elements. If the initial capacity is less than 1, an exception will be thrown. The first two construction methods are very simple. Only the third construction method is analyzed:
1 /**
2 * Creates a {@code PriorityBlockingQueue} containing the elements
3 * in the specified collection. If the specified collection is a
4 * {@link SortedSet} or a {@link PriorityQueue}, this
5 * priority queue will be ordered according to the same ordering.
6 * Otherwise, this priority queue will be ordered according to the
7 * {@linkplain Comparable natural ordering} of its elements.
8 Creates a PriorityBlockingQueue that contains elements from the specified collection.
9 If the specified set is SortedSet or PriorityQueue, the priority queue will be sorted in the same order.
10 Otherwise, this priority queue is sorted according to the natural order of its elements.
11 *
12 * @param c the collection whose elements are to be placed
13 * into this priority queue
14 * @throws ClassCastException if elements of the specified collection
15 * cannot be compared to one another according to the priority
16 * queue's ordering If the elements in the specified collection cannot be compared with each other according to the order of the priority queue
17 * @throws NullPointerException if the specified collection or any
18 * of its elements are null If the specified collection or any of its elements is empty, a NullPointerException is thrown
19 */
20 public PriorityBlockingQueue(Collection<? extends E> c) {
21 this.lock = new ReentrantLock();
22 this.notEmpty = lock.newCondition();
23 boolean heapify = true; // true if not known to be in heap order.
24 boolean screen = true; // true if must screen for nulls null check
25 if (c instanceof SortedSet<?>) { //SortedSet
26 SortedSet<? extends E> ss = (SortedSet<? extends E>) c;
27 this.comparator = (Comparator<? super E>) ss.comparator();
28 heapify = false;
29 }
30 else if (c instanceof PriorityBlockingQueue<?>) { //PriorityBlockingQueue
31 PriorityBlockingQueue<? extends E> pq = (PriorityBlockingQueue<? extends E>) c;
32 this.comparator = (Comparator<? super E>) pq.comparator();
33 screen = false;
34 if (pq.getClass() == PriorityBlockingQueue.class) // exact match
35 heapify = false;
36 }
37 Object[] a = c.toArray();
38 int n = a.length;
39 // If c.toArray incorrectly doesn't return Object[], copy it.
40 if (a.getClass() != Object[].class) //If c.toArray returns Object [] incorrectly, copy it.
41 a = Arrays.copyOf(a, n, Object[].class);
42 if (screen && (n == 1 || this.comparator != null)) { //n == 1 what the hell???
43 for (int i = 0; i < n; ++i)
44 if (a[i] == null) //Null check
45 throw new NullPointerException();
46 }
47 this.queue = a;
48 this.size = n;
49 if (heapify)
50 heapify(); //Heap, that is, it needs to be reordered according to the comparator, regardless of the order of elements before calling.
51 }The general logic of this construction method is that if the incoming collection itself has specific sorting rules, such as SortedSet and PriorityBlockingQueue, after it is converted into an array, the queue is directly pointed to the array after the possible null element verification passes. Finally, for collections of non SortedSet and PriorityBlockingQueue types, it needs to be heaped, That is, the array corresponding to the balanced binary heap structure is regenerated according to the natural sorting of elements. In short, you need to reorganize the order of array elements according to the sorting rules of PriorityBlockingQueue.
1 /**
2 * Establishes the heap invariant (described above) in the entire tree,
3 * assuming nothing about the order of the elements prior to the call.
4 Assuming that there is no change in the order of the elements before the call,
5 */
6 private void heapify() {
7 Object[] array = queue;
8 int n = size;
9 int half = (n >>> 1) - 1; //Non leaf node
10 Comparator<? super E> cmp = comparator;
11 if (cmp == null) {
12 for (int i = half; i >= 0; i--) //Traverse all non leaf nodes
13 siftDownComparable(i, (E) array[i], array, n);
14 }
15 else {
16 for (int i = half; i >= 0; i--)
17 siftDownUsingComparator(i, (E) array[i], array, n, cmp);
18 }
19 }The heap process is completed by the heapify method. This method traverses each non leaf node from bottom to top (all nodes less than half in the source code are non leaf nodes) to execute the siftDownComparable or siftDownUsingComparator. The logic of the two methods is the same. Different elements implement their own comparator methods, The other uses a unified comparator instance to compare and obtain the priority. These two methods are also one of the essence of PriorityBlockingQueue. Let's learn about this method:
siftDownComparable/siftDownUsingComparator
1 /**
2 * Inserts item x at position k, maintaining heap invariant by
3 * demoting x down the tree repeatedly until it is less than or
4 * equal to its children or is a leaf.
5 Insert item x at position k and keep the heap unchanged by repeatedly demoting x from the tree until it is less than or equal to its child element or leaf node.
6 *
7 Compare the X element with the smallest child node of K (if the left child node is larger than the right child node, take the right child node). If x is small or equal, set X as the element at k position. Otherwise, the smallest child node of K is upgraded to the parent node.
8 If the child node of k is small, continue to compare the child nodes of the child node just upgraded (if the right node is small, it is the right child node) with x to find the smallest filling, because the smallest child element of k is upgraded to the empty position,
9 Until the x element is inserted into a non leaf node or has reached the leaf node, the x is inserted into the leaf node that is finally upgraded to the parent node.
10
11 * @param k the position to fill
12 * @param x the item to insert
13 * @param array the heap array
14 * @param n heap size
15 */
16 private static <T> void siftDownComparable(int k, T x, Object[] array,
17 int n) {
18 if (n > 0) { //Queue is not empty
19 Comparable<? super T> key = (Comparable<? super T>)x;
20 int half = n >>> 1; // Loop while a non leaf node
21 while (k < half) { // k belongs to a non leaf node.
22 int child = (k << 1) + 1; // assume left child is least k
23 Object c = array[child]; // Left child node element
24 int right = child + 1; // Right child node index
25 if (right < n &&
26 ((Comparable<? super T>) c).compareTo((T) array[right]) > 0)
27 c = array[child = right]; //If the left child node is larger than the right child node, go to the smaller right child node.
28 if (key.compareTo((T) c) <= 0)
29 break; //x is smaller than the smallest child node of k, exit
30 array[k] = c; //The child node is the smallest. Upgrade its child node to the parent node.
31 k = child; //Continue to take the child node as the parent node and find the child node of the child node
32 }
33 array[k] = key; //Insert x into k
34 }
35 }The method doc of the siftDownComparable method has only one sentence: insert item x into position k, and repeatedly demote x from the tree to keep the heap unchanged until it is less than or equal to its child element or leaf node. Lines 7 to 9 are my understanding. To put it bluntly, I try to insert the X element into the k position. However, if a child node of k is smaller, I will promote the child node to the k position. Of course, X can only try to insert into the promoted child node. Similarly, if the child node of the child node is smaller than x, I have to raise the smaller grandson again, X continues to go down, and so on, Finally, either X finds a suitable position to insert in the middle, or all descendant nodes along that path are smaller than x. then x can only be inserted into the position at the end where the child nodes can be empty due to upgrade.
For example, if the ArrayList [5, 1, 4, 8, 7, 9, 0, 6, 3, 2, 9] passed in by the construction method, the order in the queue array is the same before calling the heap method, and the corresponding balanced binary tree is as follows:
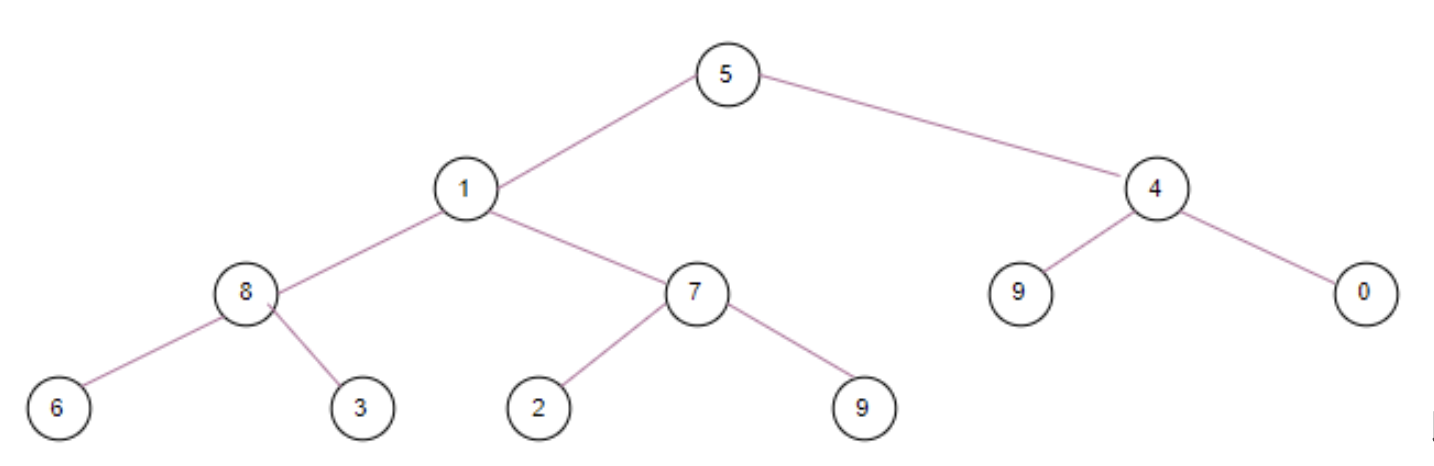
That is, from top to bottom and from left to right. Heap heap is to loop through all non leaf nodes from bottom to top. The call sequence of non leaf nodes in this example is: ⑦, ⑧, ④, ① and ⑤.
Take the penu lt imate non leaf node ⑦ as an example. If the left child node ② < the right child node ⑨, compare the left child node with ⑦. The child node is small, so ② is upgraded to the position of k, and ⑦ is inserted into the original position of ②. It has reached the bottom, so it ends. Finally, it becomes like this:
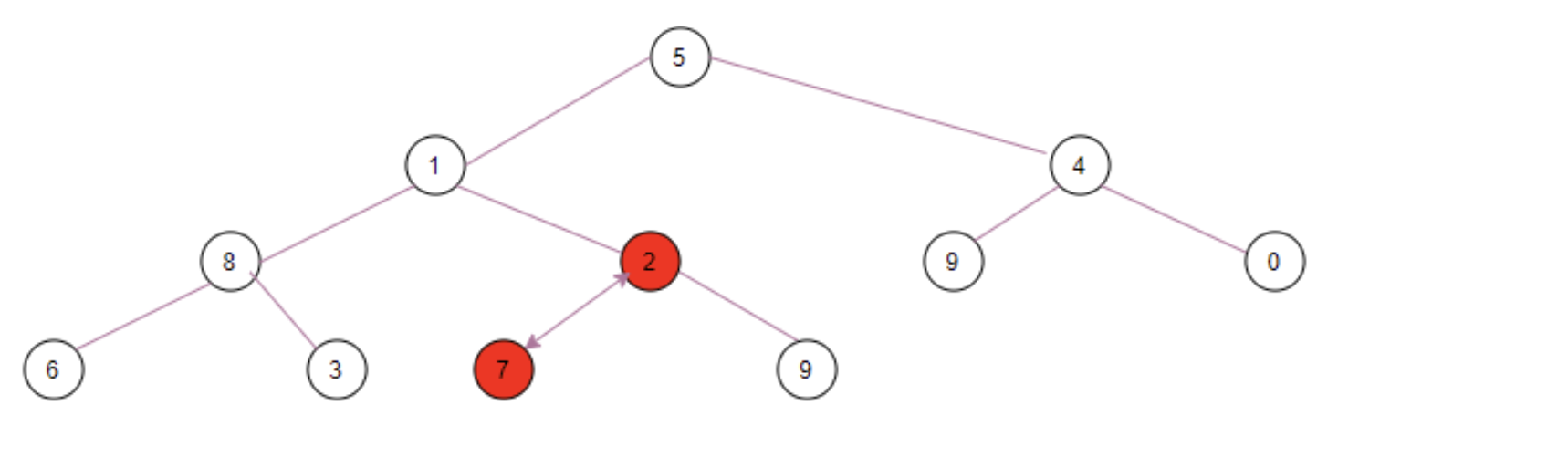
Then, the penultimate non leaf node ⑧ executes the siftDownComparable(3, 8, array, 11), the left child node ⑥ > the right child node ③, and the right child node is compared with ⑧. The child node is small again, so ③ is upgraded to position k, ⑧ is inserted into the original ③ position, and then to the bottom, and finally becomes:
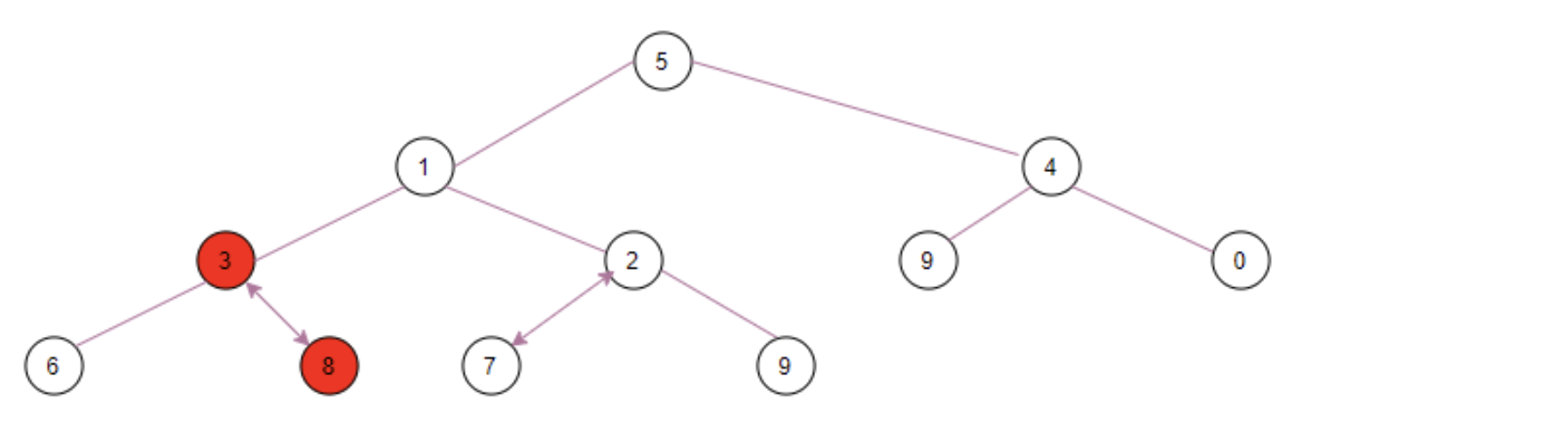
Secondly, the penultimate non leaf node ④ executes the siftDownComparable(2, 4, array, 11), the left child node ⑨ > the right child node zero, and then the right child node is compared with ④. The child node is small, so zero is upgraded to position k, ④ is inserted into the original zero position, and then to the bottom, and finally becomes:
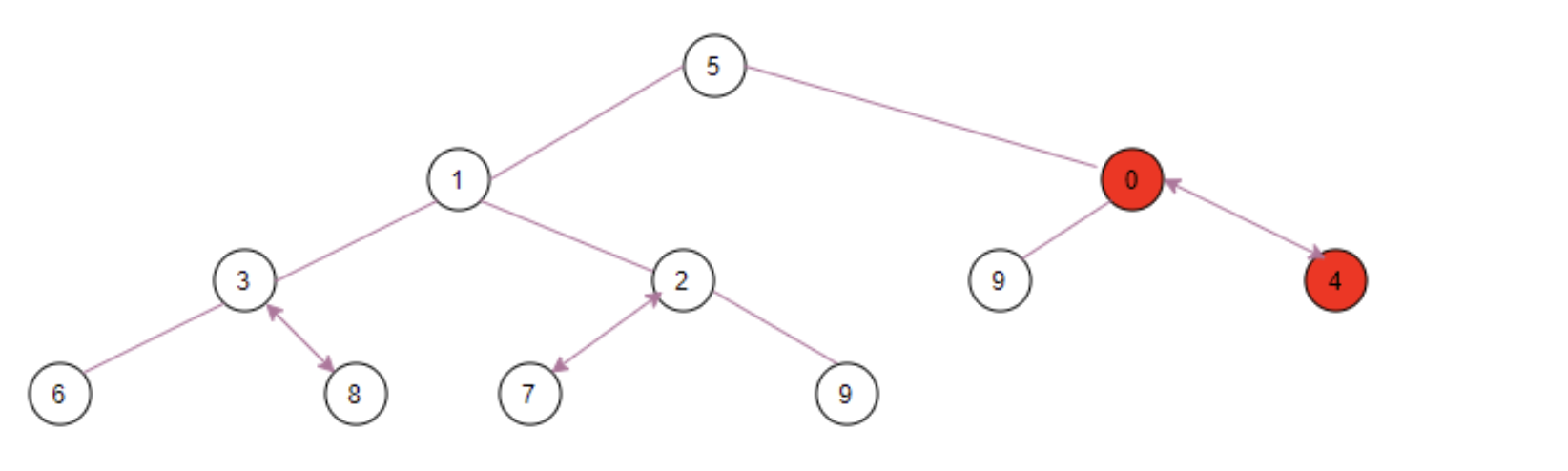
Thirdly, the penultimate non leaf node ① executes the siftDownComparable(1, 1, array, 11), the left child node ③ > the right child node ②, and the right child node is compared with ①. This time, ① is smaller, so ① is put in place without exchange, k exits the siftDownComparable method, and finally becomes unchanged.
Finally, the fifth non leaf node ⑤ executes siftDownComparable(0, 5, array, 11), and the left child node ①< If the right child node is zero, take the right child node and compare it with ⑤. The child node zero is smaller, so zero is upgraded to the K position. ⑤ is inserted into the original zero position, and K is also moved to the upgraded zero position, that is, 2. Note that ⑤ is still at the non leaf node at this time, so continue to look at its new child node. The left child node ⑨ > the right child node ④, take the right child node and compare it with ⑤, The child node is small again, so ④ is upgraded to the position of K (k==2) again, ⑤ is inserted into the original position of ④, and the leaf node has been reached. Exit the siftDownComparable method, and this time it is the top-level root node, so the heapify method also ends, and the final structure becomes:
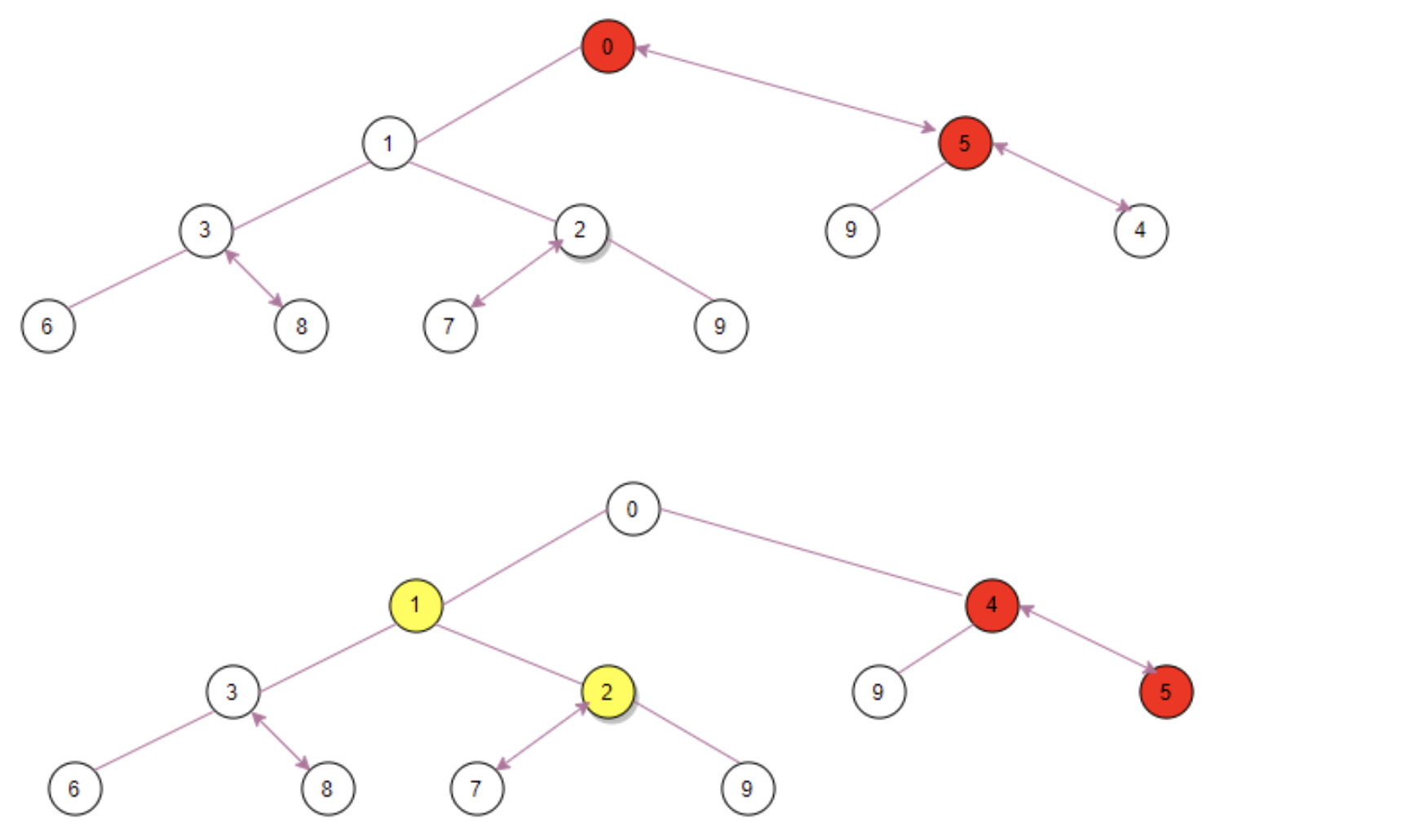
That is, the order of elements in the final array queue is: [0, 1, 4, 3, 2, 9, 5, 6, 8, 7, 9]. You can see that the elements in the queue have not completed the final real sorting. If you iterate through the iterator, the order of elements in the reaction is also out of order. Only the elements dequeued from the head of the queue through take and so on can be the really desired order (of course, the order of the set elements transferred by the drainTo method is also finally sorted), because the dequeued method will be sorted once, not the table for the time being. Let's continue to look at other methods of PriorityBlockingQueue.
Join method add/put/offer
In the end, the queue method is the offer called. Let's directly look at the source code of the offer method:
1 /**
2 * Inserts the specified element into this priority queue.
3 * As the queue is unbounded, this method will never return {@code false}.
4 * Inserts the specified element into this priority queue. Since the queue is unbounded, this method will never return false.
5
6 * @param e the element to add
7 * @return {@code true} (as specified by {@link Queue#offer})
8 * @throws ClassCastException if the specified element cannot be compared
9 * with elements currently in the priority queue according to the
10 * priority queue's ordering
11 If the specified elements cannot be compared with the elements in the current priority queue according to the order of the priority queue.
12
13 * @throws NullPointerException if the specified element is null
14 */
15 public boolean offer(E e) {
16 if (e == null)
17 throw new NullPointerException();
18 final ReentrantLock lock = this.lock;
19 lock.lock();
20 int n, cap;
21 Object[] array;
22 while ((n = size) >= (cap = (array = queue).length))
23 tryGrow(array, cap); //The actual number of elements in the queue is full. Please expand the capacity.
24 try {
25 //Start from n (the end) and look up for a grandfather node that is just smaller or equal to it,
26 //Then insert it below the parent node (as its child node)
27 Comparator<? super E> cmp = comparator;
28 if (cmp == null)
29 siftUpComparable(n, e, array);
30 else
31 siftUpUsingComparator(n, e, array, cmp);
32 size = n + 1; //size plus 1
33 notEmpty.signal(); //Wake up potentially blocked consumer threads
34 } finally {
35 lock.unlock();
36 }
37 return true;
38 }There are two important points in the offer method of queue operation. The first is that if the queue is full of size (actual number of elements) > = queue. Length (current array length), it needs to be expanded until the expansion is successful or OutOfMemoryError is thrown; The second is the implementation of the siftUpComparable/siftUpUsingComparator method.
Let's first look at the expansion method:
1 /**
2 * Tries to grow array to accommodate at least one more element
3 * (but normally expand by about 50%), giving up (allowing retry)
4 * on contention (which we expect to be rare). Call only while
5 * holding lock.
6 Try to expand the array to accommodate at least one element (but usually expand by 50%) and give up on contention (retry is allowed) (we hope this is rare).
7 Called only when the lock is held.
8 *
9 * @param array the heap array
10 * @param oldCap the length of the array
11 */
12 private void tryGrow(Object[] array, int oldCap) {
13 lock.unlock(); // Must release and then re acquire main lock.
14 Object[] newArray = null;
15 if (allocationSpinLock == 0 &&
16 UNSAFE.compareAndSwapInt(this, allocationSpinLockOffset,
17 0, 1)) { //CAS's ability to obtain capacity expansion indicates that I want to expand capacity
18 try {
19 int newCap = oldCap + ((oldCap < 64) ?
20 (oldCap + 2) : // If the capacity is small, expand more.
21 (oldCap >> 1));//It has exceeded 64, expanding only half at a time
22 if (newCap - MAX_ARRAY_SIZE > 0) { // possible overflow exceeds the maximum limit
23 int minCap = oldCap + 1;
24 if (minCap < 0 || minCap > MAX_ARRAY_SIZE)
25 throw new OutOfMemoryError(); //It is already the largest. Throw OutOfMemoryError
26 newCap = MAX_ARRAY_SIZE; //Otherwise, expand the capacity to the maximum allowable limit
27 }
28 if (newCap > oldCap && queue == array) //The expansion is successful, and the current source array is not expanded by other threads.
29 newArray = new Object[newCap]; //Create a new array
30 } finally {
31 allocationSpinLock = 0; //After capacity expansion, restore the mark
32 }
33 }
34 if (newArray == null) // back off if another thread is allocating
35 Thread.yield(); //Just another thread is already expanding. Give up the CPU
36 lock.lock(); //You really need to start capacity expansion to obtain the lock,
37 if (newArray != null && queue == array) {//The new array has been applied for and has not been expanded by other threads
38 queue = newArray; //Change the current array to point to the new array
39 System.arraycopy(array, 0, newArray, 0, oldCap); //Copy element
40 }
41 }The logic of capacity expansion is very simple. Before calculating the size of this capacity expansion, first release the unique lock so that other consuming threads will not be blocked, so that subsequent queued threads will not be blocked after the queue is dissatisfied due to consumption, and then compete for the execution right of capacity expansion through an allocationSpinLock, The thread that gets this flag can calculate how large it should be expanded this time, otherwise it will sell the CPU; After the thread that gets the tag calculates the length of the new array, it still needs to obtain the unique lock before performing the array expansion operation (that is, copy the original array to the new array and make the queue point to the new array). Interestingly, if the capacity of the queue is less than 64 at the beginning, it will be expanded twice each time. Otherwise, it will be expanded by half. After all, the resources will be more strained later. The essence of capacity expansion is to try not to block other incoming and outgoing operations. Other operations will be blocked only when copying data to a new array.
When trygrow offer s, it locks, so it comes in and unlocks. It does not block other consumer threads, but only copies the data and then blocks
Let's look at the queue logic: siftUpComparable/siftUpUsingComparator
The siftDownXXX method described above is one of the essence of PriorityBlockingQueue. The other is the two siftUpXXX methods. These two groups of methods are the core of the balanced binary heap sorting algorithm implemented by PriorityBlockingQueue.
/**
2 * Inserts item x at position k, maintaining heap invariant by
3 * promoting x up the tree until it is greater than or equal to
4 * its parent, or is the root.
5 Insert item x at position k and keep the heap unchanged by lifting x up until it is greater than or equal to its parent or root element.
6 *
7 * To simplify and speed up coercions and comparisons. the
8 * Comparable and Comparator versions are separated into different
9 * methods that are otherwise identical. (Similarly for siftDown.)
10 * These methods are static, with heap state as arguments, to
11 * simplify use in light of possible comparator exceptions.
12 Simplify and accelerate forcing and comparison. The Comparable and Comparator versions are divided into different methods, which are otherwise the same.
13 * These methods are static and use heap state as a parameter to simplify use based on possible comparator exceptions.
14
15 siftUp Starting from k, find a grandfather node that is just smaller or equal to it, and then insert it below the grandfather node (as its child node).
16 In the process of searching, the position of the grandfather node larger than it will also be moved down.
17
18 * @param k the position to fill Filling position
19 * @param x the item to insert Item to insert
20 * @param array the heap array Heap array
21 */
22 private static <T> void siftUpComparable(int k, T x, Object[] array) {
23 Comparable<? super T> key = (Comparable<? super T>) x;
24 while (k > 0) {
25 int parent = (k - 1) >>> 1; //Parent node index
26 Object e = array[parent]; //Parent node element
27 if (key.compareTo((T) e) >= 0) //Find a parent node smaller than or equal to the key and jump out of the loop
28 break;
29 array[k] = e; //Move parent node down
30 k = parent; //Continue to find the parent node of the parent node
31 }
32 array[k] = key; //Insert x below its smaller or equal parent node (as its child node).
33 }The siftUpComparable method is to try to insert x into the k position. If x is larger than the parent node of the k position node, X should occupy the k position. Otherwise, demote the parent node to the k position, and X rises to the position of the previous parent node, and then continue to compare its new parent node. If x is still smaller than the new parent node at this time, continue to demote the new parent node to the x position, X is upgraded to this position again until x finds that it is greater than or equal to its parent node or X has reached the top and become the root node. In fact, it is a process that x starts from the last element. Take the above queue status [0, 1, 4, 3, 2, 9, 5, 6, 8, 7, 9] as an example. What happens if offer(3), that is, join a 3?
According to the offer method, the capacity at this time is just equal to the default initial capacity, so first double the capacity to 11 + (11 + 2) = 24. Then execute the siftUpUsingComparator(11, 3, array), insert 3 into the position of 11, that is, the lowest row of the binary tree. ② there are already two child nodes. ⑨ has no child nodes, so insert it below ⑨ as its left child node first:
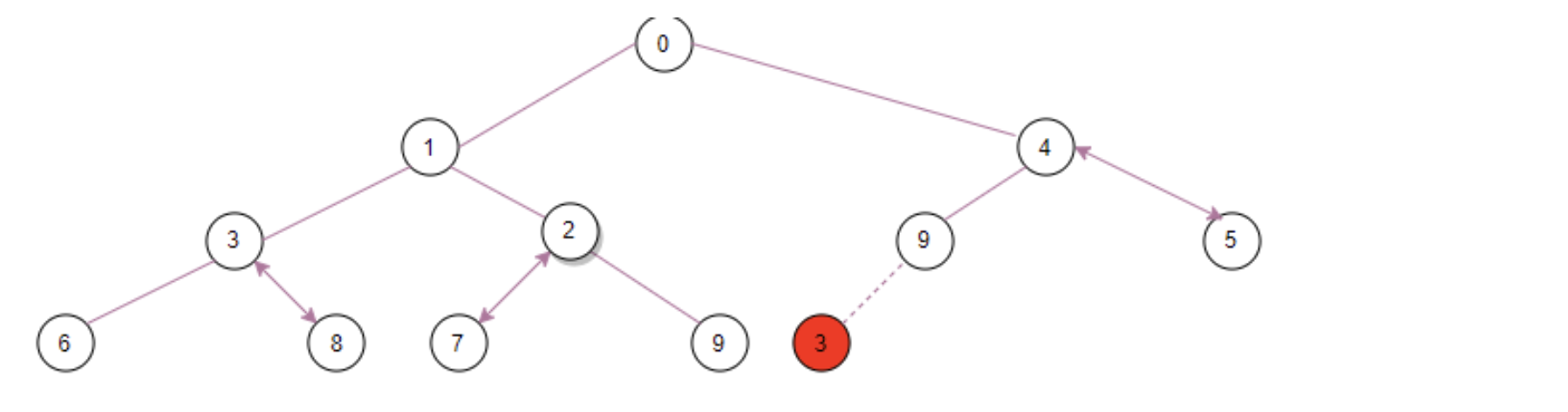
Then ③ is smaller than its parent node ⑨, so ③ and ⑨ are transposed to become:
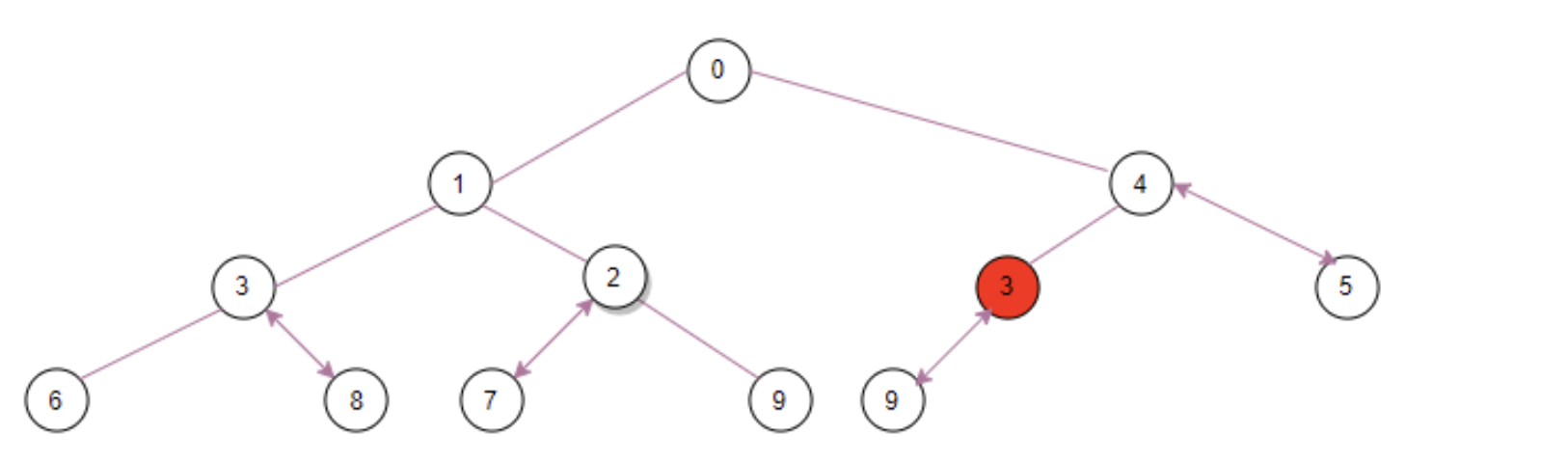
Continue to look at the new parent node ④, or ③ is smaller, so ③ and ④ are transposed to become:
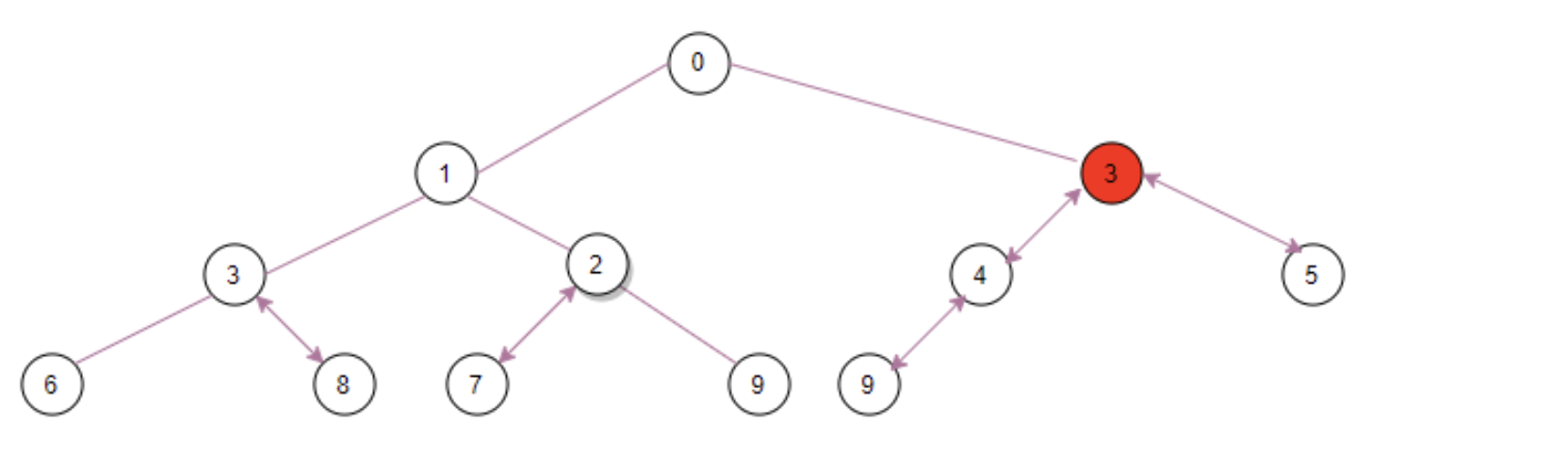
Finally, ③ is larger than its parent node zero, so ③ occupies this position and ends. Finally, the array becomes [0, 1, 3, 3, 2, 4, 5, 6, 8, 7, 9, 9]. The algorithm of siftUpXXX is to first try to insert x into k and find a really suitable position of X by bubbling upward. In the queue entry operation offer, you insert a new element into the end of the queue, and then adjust your position by bubbling up.
take/poll
Except peek, because it is the first element of the array to be obtained but not deleted, multiple calls to peek return the same value. For example, no matter how many times you execute peek in succession, you will get queue[0], i.e. 0. take and poll are the real out of queue methods. When the queue is empty, poll() immediately returns null, For other blocking methods, the waiting queue is not empty or timeout. The dequeue method is called by the real outgoing logic:
1 /**
2 * Mechanics for poll(). Call only while holding lock. Called only when locked
3 */
4 private E dequeue() {
5 int n = size - 1;
6 if (n < 0) //There are no more elements
7 return null;
8 else {
9 Object[] array = queue;
10 E result = (E) array[0]; //Take the first element
11 E x = (E) array[n]; //Last element
12 array[n] = null; //Empty the last element position
13 Comparator<? super E> cmp = comparator;
14 if (cmp == null)
15 siftDownComparable(0, x, array, n);
16 else
17 siftDownUsingComparator(0, x, array, n, cmp);
18 size = n; //Modify size
19 return result;
20 }
21 }Out of the logic of the team: first take away the first element of queue[0] directly, because the queue has ensured that the most top root node is the smallest element when the team is joined, but other nodes are not necessarily arranged in sequence. After taking the first element, the last element is also taken out, and then the siftDownXXX method is called. Try to put the last element in the position of queue [0]. Of course, the last element is not the smallest in 90% of the cases, so siftdownxxx will constantly degrade it to promote the really smallest element to the position of queue [0].
Take the above example [0, 1, 3, 3, 2, 4, 5, 6, 8, 7, 9, 9], for example, the first call to take() returns 0, and then put the last element ⑨ in the position of queue[0]:
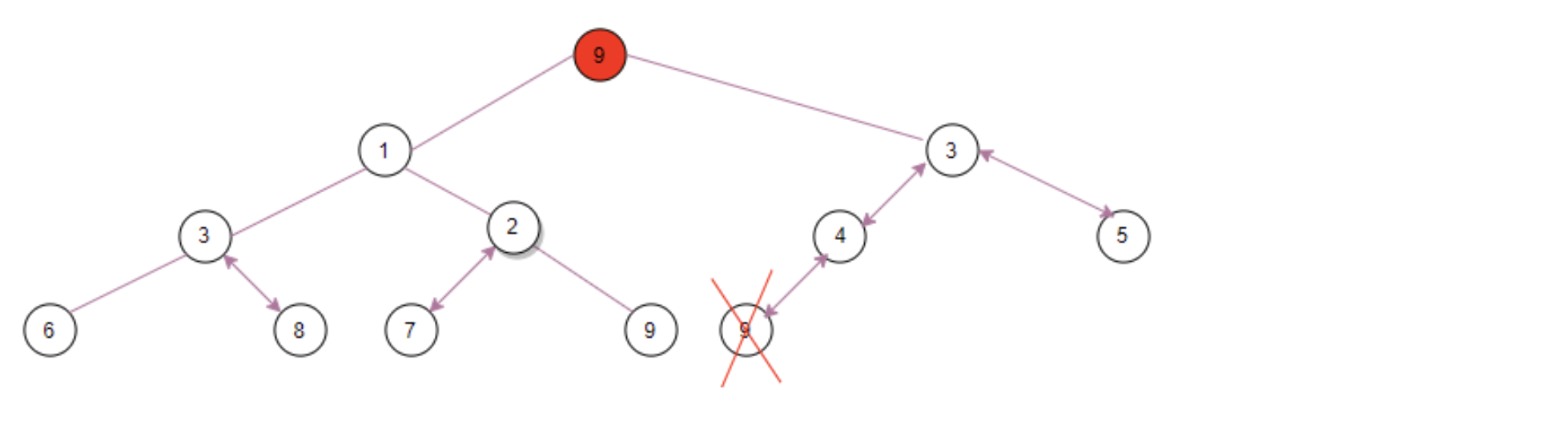
Then, the left child node ① of ⑨ is less than the right child node ③. Compared with ⑨, the left child node ① is smaller, so the exchange positions of ① and ⑨ are: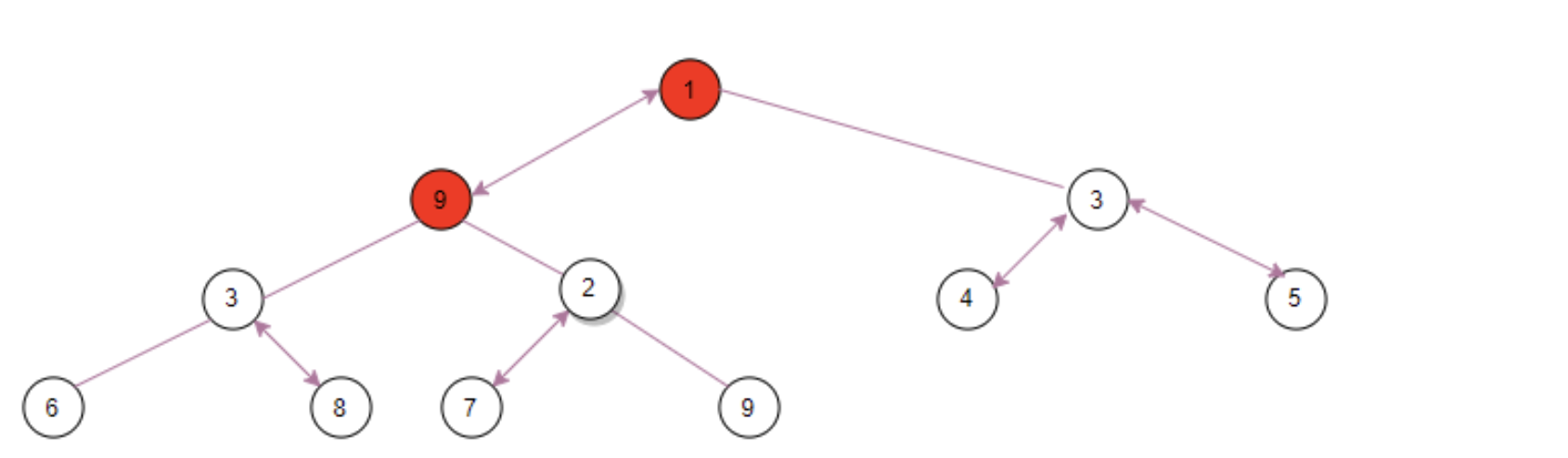
Secondly, if the left child node ③ of ⑨ > the right child node ②, take the right child node ② and ⑨ In comparison, the right child node is smaller, so exchange ② and ⑨ exchange positions: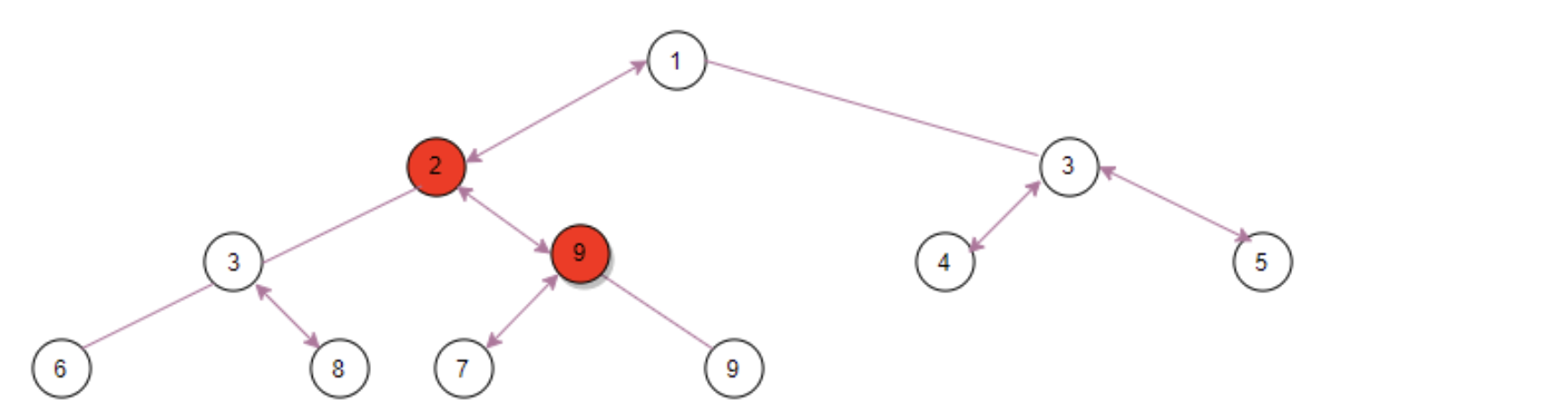
Finally, if the left child node ⑦ of ⑨ is less than the right child node ⑨, take the left child node ⑦ and ⑨ In comparison, the left child node is smaller, so the exchange positions of ⑦ and ⑨ are: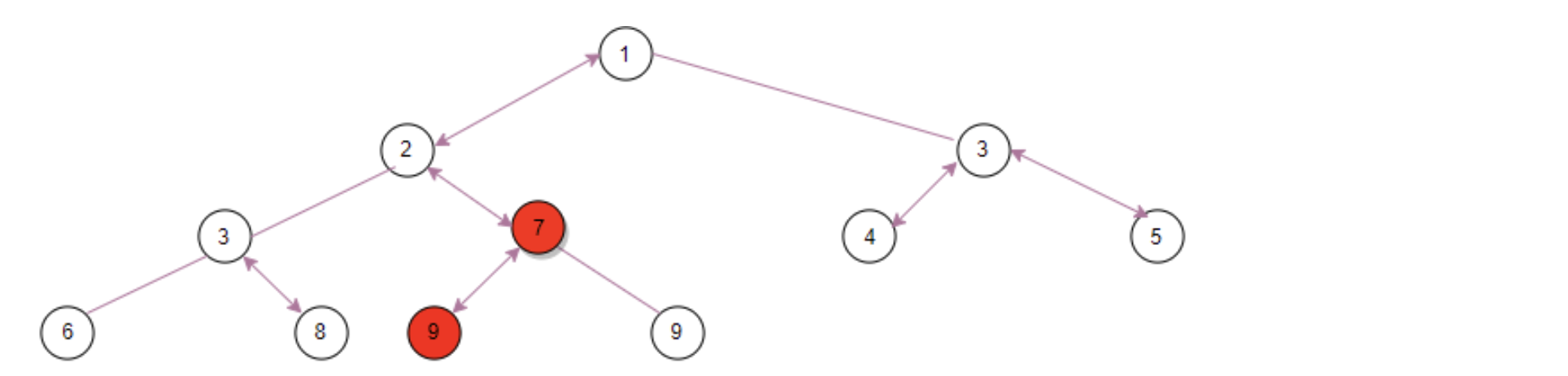
Since then, the leaf node has been reached, and the take method really returns only after the siftDownXXX method is completed. Therefore, when taking away the smallest queue[0] element every time take is executed, the smallest of the remaining elements will be bubbled to the queue[0] position for the next queue exit, and so on. The next return will be prepared every time take is called, Instead of being in order when you join the team, this may be to save unnecessary execution. So far, the entry and exit logic of PriorityBlockingQueue has been clear.
remove(Object)
Another complex method is to delete remove(Object) internally. It first gets the corresponding index through indexOf(Object) traversal, and then uses the removeAt(index) method to really execute the deletion logic. Look at removeAt directly:
1 /**
2 * Removes the ith element from queue.Deletes the i th element from the queue
3 */
4 private void removeAt(int i) {
5 Object[] array = queue;
6 int n = size - 1;
7 if (n == i) // removed last element deletes the last element
8 array[i] = null;
9 else {
10 E moved = (E) array[n]; //Last valid element
11 array[n] = null; //Empty the position of the last valid element
12 Comparator<? super E> cmp = comparator;
13
14 //Try overwriting the i position with the last element and demoting down to adjust the position.
15 if (cmp == null)
16 siftDownComparable(i, moved, array, n);
17 else
18 siftDownUsingComparator(i, moved, array, n, cmp);
19
20 //If there is no adjustment down, you need to bubble up and try adjustment again.
21 if (array[i] == moved) {
22 if (cmp == null)
23 siftUpComparable(i, moved, array);
24 else
25 siftUpUsingComparator(i, moved, array, cmp);
26 }
27 }
28 size = n;
29 }When removing, if the last element is deleted, the queue[i] is directly set to empty. If the last element is not deleted, the last element is taken away. First, execute siftDown to directly overwrite the last element to the I position, and then demote down through siftUp to adjust the position. If there is no adjustment, that is, the last element is still in the I position, Then bubble up to adjust your position. At the same time, siftDown and siftUp are used to adjust the structure of binary heap.
Other methods are simple, so I won't list them one by one. Since PriorityBlockingQueue is unbounded, calling remainingCapacity() always returns Integer.MAX_VALUE. The toArray method copies the elements in the current array and returns them to a new array, so the returned array is not sorted and will not have any impact on the source queue. When the drainTo method performs the element transfer, the dequeue method is executed for each element transferred to sort the binary heap, so the array returned by drainTo is sorted. The array passed in by drawnto will be overwritten by the queue element, and the positions exceeding the queue length will be reset to null.
As for the order of elements with the same priority, PriorityBlockingQueue itself does not guarantee the order of such elements, but you can define a wrapper class or a new comparator to implement it. The two elements Student and Person objects in the following example are sorted according to age, When the age is the same, the PriorityBlockingQueue has the same priority. At this time, it is unpredictable who comes first. However, we can redefine a wrapper class and rely on the second attribute to process the order of elements with the same priority:
1 package com.Queue;
2
3 import java.util.concurrent.PriorityBlockingQueue;
4 import java.util.concurrent.atomic.AtomicLong;
5
6 /**
7 * <E extends Comparable> Is an upper limit wildcard. The accepted type E must implement the Comparable interface.
8 * <? super E> Is the lower limit wildcard to limit the accepted type? Must be a parent of E.
9 * <E extends Comparable<? super E>> Taken together, it means accepting type E and its parent types that implement the Comparable interface and can be compared with its parent class.
10 * To put it bluntly, it can be a parent-child relationship type that can be compared between father and father, son and son, and between father and son
11 *
12 * @param <E>
13 */
14 public class FIFOEntry<E extends Comparable<? super E>> implements Comparable<FIFOEntry<E>> {
15
16 static final AtomicLong seq = new AtomicLong(0);
17 final long seqNum;
18
19 final E entry;
20
21 public FIFOEntry(E entry) {
22 seqNum = seq.getAndIncrement();
23 this.entry = entry;
24 }
25
26 public E getEntry() {
27 return entry;
28 }
29
30 public int compareTo(FIFOEntry<E> other) {
31 int res = entry.compareTo(other.entry);
32 if (res == 0 && other.entry != this.entry)
33 res = (seqNum < other.seqNum ? -1 : 1);
34 return res;
35 }
36
37 @Override
38 public String toString() {
39 return "FIFOEntry{" +
40 "seqNum=" + seqNum +
41 ", entry=" + entry +
42 '}';
43 }
44
45 public static void main(String[] args) throws Exception{
46
47 FIFOEntry tom = new FIFOEntry(new Student(12, "Tom"));
48
49 FIFOEntry tony = new FIFOEntry(new Person(12, "Tony"));
50
51 PriorityBlockingQueue<FIFOEntry> pbQueue = new PriorityBlockingQueue<>();
52
53 pbQueue.offer(tony);
54 pbQueue.offer(tom);
55
56 System.out.println(pbQueue.take());//FIFOEntry{seqNum=0, entry=Student{age=12, name='Tom'}}
57 System.out.println(pbQueue.take());//FIFOEntry{seqNum=1, entry=Person{age=12, name='Tony'}}
58
59 }
60 }
61
62 class Person implements Comparable<Person> {
63
64 Integer age;
65
66 String name;
67
68 public Person(Integer age, String name) {
69 this.age = age;
70 this.name = name;
71 }
72
73 @Override
74 public int compareTo(Person o) {
75 return this.age.compareTo(o.age);
76 }
77
78 @Override
79 public String toString() {
80 return "Person{" +
81 "age=" + age +
82 ", name='" + name + '\'' +
83 '}';
84 }
85 }
86
87
88 class Student extends Person {
89
90 public Student(Integer age, String name) {
91 super(age, name);
92 }
93
94 @Override
95 public String toString() {
96 return "Student{" +
97 "age=" + age +
98 ", name='" + name + '\'' +
99 '}';
100 }
101 }The second attribute seq that determines the sorting order in the above example is a static atomic variable, so whoever constructs the FIFOEntry instance first has a higher priority. Therefore, although the order of joining the queue is tony and tom, the order of leaving the queue is always tom with a higher priority.
summary
PriorityBlockingQueue is an unbounded blocking queue, but the capacity is gradually expanded with insufficient element space. It only supports the placement of comparable objects, that is, elements that directly or indirectly implement the Comparator interface. PriorityBlockingQueue uses array based balanced binary heap to store queue elements, After the elements are queued, the order in the internal array is not really arranged according to priority. Only the element sequence queued through take, poll method or drawto is really arranged according to priority. The iterative order of iterator iterator or separable iterator is not sorted according to priority, and the iterators are not synchronized with the changes of the original queue.
PriorityBlockingQueue adopts the same sorting algorithm as PriorityQueue, that is, balanced binary heap. However, PriorityBlockingQueue is thread safe. It does not rely on any PriorityQueue method. It only stores the queue sequence and deserialization according to PriorityQueue for compatibility. Although PriorityQueue and PriorityBlockingQueue adopt the same algorithm and the same internal mechanism, their iterators are different. The iterator of PriorityQueue directly iterates the original queue array, while the data of PriorityBlockingQueue iterator is copied from the original queue array, It has been separated from the original data source.