1, What is Prim algorithm
The process of finding the minimum spanning tree by prim algorithm adopts the idea of greedy algorithm. For a connected network with N vertices, PRIM algorithm finds an edge with the smallest weight from the connected network every time. This operation is repeated N-1 times. The spanning tree composed of N-1 edges with the smallest weight is the minimum spanning tree.
2, Prim implementation ideas
- All vertices in the connected network are divided into two categories (assuming class A (nodes have been accessed) and class B (nodes have not been accessed). first In the initial state, all vertices are in class B;
- Select any vertex and move it from class B to class A; (mark this node as accessed)
- Starting from all vertices of class B, find an edge connecting a vertex in class A with the smallest weight, and move the vertex in class a connected by this edge to class B (double loop, find the smallest edge between access node and non access node)
- Repeat step 3 Step until all vertices in class B move to class A, and N-1 edges can be found. (cycle realization constitutes n-1 times)
If starting from vertex A, the weights from vertex B, C, D to vertex A are 2, 4 and 2 respectively. Therefore, for vertex A, the weights of vertex B and vertex d to A are the smallest. Suppose that the vertex B found first:
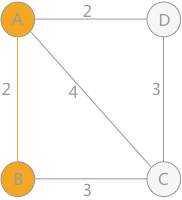
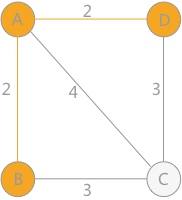
Continue to analyze vertices C and D. the weight from vertex C to B is 3 and the weight from vertex A is 4; the weight from vertex d to a is 2 and the weight from vertex B is infinite (if there is no direct path between them, set the weight to infinity). Therefore, the weight from vertex d to a is the smallest:
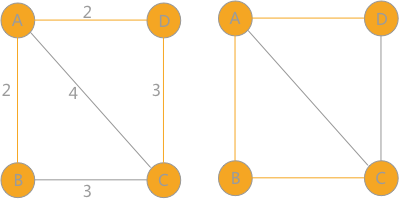
Finally, only vertex C is left, the weight to A is 4, and the weight to B is as large as that to D, which is 3. Therefore, the connected graph has two minimum spanning trees:
3, Prim application example and code implementation
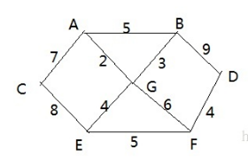
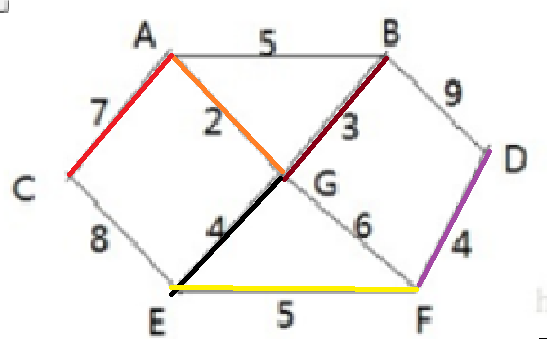
Problem Description: there are 7 villages (A, B, C, D, E, F, G) in Shengli township. Now roads need to be built to connect the 7 villages
* The distance of each village is represented by A sideline (right), for example, A – B is 5km away.
* Ask: how to build roads to ensure that all villages can be connected and the total mileage of roads built is the shortest?
Realization idea
For example, starting from point A, the steps of PLIM algorithm are as follows:
1. Start processing from the < a > vertex, A-C [7] A-G[2] A-B[5], select the smallest < A, G >, and mark the two points as selected
2. Start with < A, G > and process the vertices a and G and their adjacent vertices that have not been accessed. A-C[7] A-B[5] G-B[3] G-E[4] G-F[6] Select the smallest < A, G, b > and mark as selected
3. < A,G,B > start, process the vertices A,G,B and their adjacent vertices that have not been accessed A-C[7] G-E[4] G- F[6] B-D[9] Select the smallest < A,G,B, E > and mark it as selected. And so on. Finally, you will get:
4. {a, G, B, e} - > F / / the 4th large cycle, Corresponding edge < e, f > weight: 5
5. {a, G, B, e, f} - > D / / the 5th large cycle, corresponding edge < F, d > weight: 4
6. {a, G, B, e, F, D} - > C / / the 6th large cycle, corresponding edge < A, C > weight: 7 = = = > < A, G, B, e, F, D, C >
code implementation
package c13prim;
import java.util.Arrays;
public class Prim {
//Use a large number to indicate that there is no connection between the two points
public static final int N = 100;
public static void main(String[] args) {
char[] vertexs = new char[]{'A', 'B', 'C', 'D', 'E', 'F', 'G'};
//An array is used to represent the adjacency matrix, and N represents unconnected
int[][] weight = new int[][]{
{N, 5, 7, N, N, N, 2},
{5, N, N, 9, N, N, 3},
{7, N, N, N, 8, N, N},
{N, 9, N, N, N, 4, N},
{N, N, 8, N, N, 5, 4},
{N, N, N, 4, 5, N, 6},
{2, 3, N, N, 4, 6, N}};
Graph graph = new Graph(vertexs, weight);
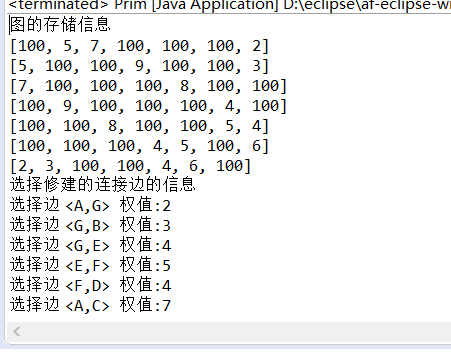
System.out.println("Storage information of graph");
graph.showGraph();
System.out.println("Information about the selected connecting edge");
graph.prim(0);
}
static class Graph{
private char[] vertex; //Represents vertex information
private int[][] edges; //Store the adjacency matrix to represent the weight between edges
public Graph(char[] vertex,int[][] edges) {
this.vertex =vertex;
this.edges = edges;
}
public void showGraph(){
for (int[] edge : edges) {
System.out.println(Arrays.toString(edge));
}
}
//Build Prim algorithm and realize the code according to the idea
public void prim( int VertexIndex) {
//Mark whether the vertex has been selected. If it is selected, it is 1 and if it is not selected, it is 0
int[] selected = new int[vertex.length];
//Marks the current vertex as selected
selected[VertexIndex] = 1;
//Subscript of accessed vertex
int visitYesIndex = -1;
//The subscript of the vertex has not been accessed
int visitNoIndex = -1;
//Initialize the minimum weight to an unreachable number
int minWright = N;
int length=vertex.length;
//Why start from 1? Because after the prim algorithm, k vertices and k-1 edges can only be generated
for (int k = 1; k < length; k++) {
//You need to traverse the selected vertices every time. For example, only point A has been selected in the first traverse, A and G in the second, A, G, B in the third, and the fourth
for (int i = 0; i < length; i++) {
//Each time, you need to traverse the vertices that have not been selected. For example, when i corresponds to A, j corresponds to C, G and B (excluding unreachable vertices)
for (int j = 0; j < length; j++) {
//If i is selected, j is unselected, and i and j are reachable (with edges)
if (selected[i] == 1 && selected[j] == 0 && edges[i][j] < minWright) {
//Replace minWeight to find the smallest edge of the weights of the vertices that have been accessed and the vertices that have not been accessed
minWright = edges[i][j];
// Replace selected and unselected vertices that match the criteria for each comparison
visitYesIndex = i;
visitNoIndex = j;
}
}
}
//After a loop, the smallest edge is obtained. At this time, the unreachable edge should be set as accessed
System.out.println("Select edge <" + vertex[visitYesIndex] + "," +vertex[visitNoIndex] + "> Weight :" + minWright);
selected[visitNoIndex] = 1;
//minWright resets the maximum value
minWright = N;
}
}
}
}
Result display