Prefix sum and difference array
Basic concepts
- Prefix and
We have an array. If we want to know the sum of interval [L, R], the usual way is to traverse it; This may be possible when the number of visits is relatively small, but when we need multiple visits, if we visit m times, the time complexity is O(m * n).
The prefix sum (space for time) is used to construct an array sum, and the array elements record the sum of the array elements before the index (including the index). We only need sum[R] - sum[L - 1] to find the sum of the specified ranges. If M visits are made, the time complexity is O(m).
for (int i = 1; i <= n; i++) {
sum[i] = sum[i - 1] + arr[i];
}
- Differential array
If we need to increase or decrease an interval of the array frequently, the usual method is to increase or decrease while traversing. The time complexity of this method is O(N). By introducing the difference array, we only need the time complexity of O(1).
for (int i = 1; i < n; i++) {
diff[i] = nums[i] - nums[i - 1];
}
Leetcode example
303. Region and retrieval - array immutable
Train of thought analysis:
We define an array sum ourselves, and set sum [0] to 0. Sum [i] represents the cumulative sum from num[0] to num[i - 1].
class NumArray {
public:
vector<int> sums;
NumArray(vector<int>& nums) {
int len = nums.size();
sums.resize(len + 1);
for (int i = 1; i <= len; i++) {
sums[i] = sums[i - 1] + nums[i - 1];
}
}
int sumRange(int left, int right) {
return sums[right + 1] - sums[left];
}
};
Train of thought analysis:
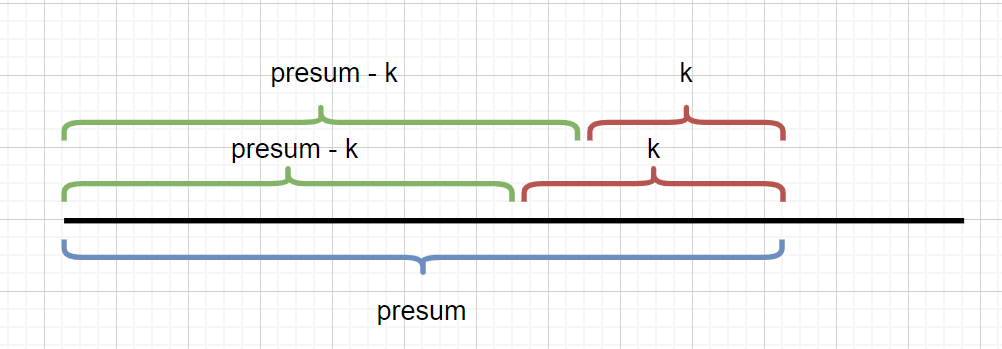
pre[j - 1] == pre[i] - k
When we consider the number of consecutive subarrays ending with I and K, we only need to count the number of prefixes and pre[j] with pre[i] - K. We establish a hash table mp, with and as the key, the number of occurrences as the corresponding value, record the number of occurrences of pre[i], update the mp edge from left to right, and calculate the answer, then the answer mp[pre[i] - k] ending with I can be obtained in O(1) time. The final answer is the sum of the number of subarrays with k at the end of all subscripts.
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
unordered_map<int, int> hash;
int sum = 0, cnt = 0;
hash[0] = 1;
for (int i = 0; i < nums.size(); i++) {
sum += nums[i];
if (hash[sum - k]) cnt += hash[sum - k];
hash[sum]++;
}
return cnt;
}
};
304. Two dimensional area and retrieval - the matrix is immutable
Train of thought analysis:
Solution to the problem of negative snow and bright candle
class NumMatrix {
public:
vector<vector<int>>preSum;
NumMatrix(vector<vector<int>>& matrix) {
if(matrix.empty()){
return ;
}
int n=matrix.size();
int m=matrix[0].size();
preSum.resize(n+1);
for(int i=0;i<n+1;i++){
preSum[i].resize(m+1);
}
if (n> 0) {
for (int i = 0; i <n; i++) {
for (int j = 0; j <m; j++) {
preSum[i+1][j+1] = preSum[i][j+1] + preSum[i+1][j] - preSum[i][j] + matrix[i][j];
}
}
}
}
int sumRegion(int row1, int col1, int row2, int col2) {
return preSum[row2 + 1][col2 + 1] - preSum[row2 + 1][col1] - preSum[row1][col2 + 1] + preSum[row1][col1];
}
};
class Solution {
public:
bool carPooling(vector<vector<int>>& trips, int capacity) {
if (trips.empty()) {
return false;
}
const int MAX_PASSNUM = 1001;
vector<int> changeNum(MAX_PASSNUM, 0);
for (int i = 0; i < trips.size(); i++) {
changeNum[trips[i][1]] += trips[i][0];
changeNum[trips[i][2]] -= trips[i][0];
}
int sum = 0;
for (int j = 0; j < changeNum.size(); j++) {
sum += changeNum[j];
if (sum > capacity) {
return false;
}
}
return true;
}
};
1109. Flight reservation statistics
class Solution {
public:
vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
vector<int> relust(n+1, 0);
int diff = 0;
for(int i = 0; i < bookings.size(); i++){
int k = bookings[i][0]-1;
diff = bookings[i][2];
relust[k] += diff;
int j = bookings[i][1];
relust[j] -= diff;
}
for(int i = 1; i < n; i++){
relust[i] += relust[i-1];
}
relust.pop_back();
return relust;
}
};
Original address: http://www.bcysf.cn/index.php/archives/6/