Title Description

Given a ring with N nodes, numbered 1.N, the points on the ring have weights (positive or negative). Now we need to dynamically modify the weights of a point to find the maximum continuous sum on the ring after each modification, but not the sum of the whole sequence.

Input format

The first action is an integer N (4<=N<=100000).
The second action is N integers separated by spaces.
The third action is an integer M (4<=M<=100000), which indicates the number of modifications (absolute value is less than 1000).
Next, in line M, two integers A and B (-1000<=B<=1000) are used for each line, indicating that the value of the number A in the sequence is changed to B.

Output format

For each modification, the maximum continuous sum on the modified ring is output.

Sample data

sample input

5
3 -2 1 2 -5
4
2 -2
5 -5
2 -4
5 -1

sample output

4
4
3
5

Title Analysis

It's a bit difficult.
Preparatory knowledge: the maximum continuity on the ring and the maximum sum on the chain can be converted to max {the maximum sum on the chain, all the numbers minus the minimum sum on the chain}
Why?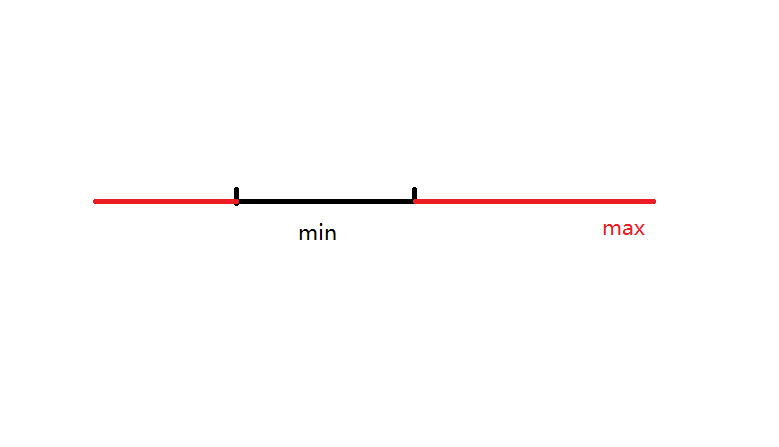

Because if the maximum crosses the chain, then the minimum must be on the chain, and the complement is the largest, otherwise the maximum can swallow part of the larger.
Then we can use segment tree to maintain the sum of segments, the maximum sum of segments and the minimum sum of segments.
However, we will find that only these three attributes can not complete tag upload.
Because the greatest and smallest of fathers may not only come from the greatest and smallest of sons, but also have parts of each.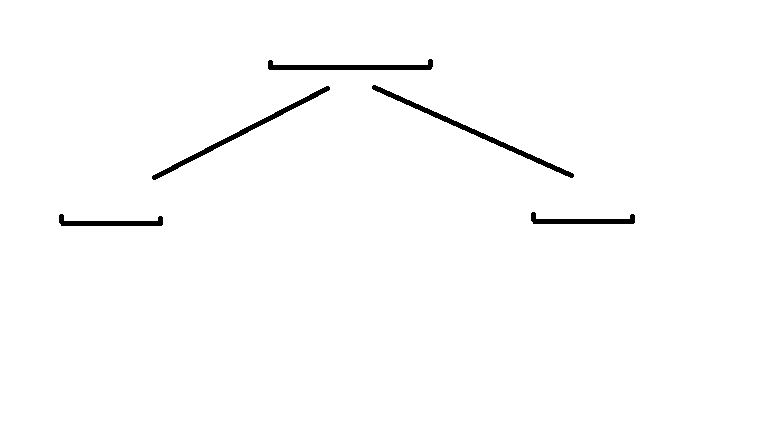

Therefore, we also need to maintain the maximum and minimum sums from the left endpoint to the right, and the maximum and minimum sums from the right endpoint to the left.
Then we can mark up the upload.
father.sum=lc.sum+rc.sum
father.leftmax=max(lc.leftmax,lc.sum+rc.leftmax)
father.rightmax=max(rc.rightmax,rc.sum+lc.rightmax)
father.summax=max(lc.summax,rc.summax,lc.rightmax+rc.leftmax
Attribute equivalence of min

Maintain more attributes, pay attention not to write wrong

source code

#include<algorithm>
#include<iostream>
#include<iomanip>
#include<cstring>
#include<cstdlib>
#include<vector>
#include<cstdio>
#include<cmath>
#include<queue>
using namespace std;
inline const int Get_Int() {
    int num=0,bj=1;
    char x=getchar();
    while(x<'0'||x>'9') {
        if(x=='-')bj=-1;
        x=getchar();
    }
    while(x>='0'&&x<='9') {
        num=num*10+x-'0';
        x=getchar();
    }
    return num*bj;
}
const int maxn=100000;
struct Tree { //Point Modified Interval Query
    int left,right,sum; //sumRepresents the sum of the current paragraph
    int leftmax,rightmax,summax; //leftmaxRepresents the largest sum from left. rightmax Represents the largest sum from the right. summax Represents the maximum sum
    int leftmin,rightmin,summin; //Empathy
};
struct Segment_Tree {
    Tree tree[maxn*4];
    void build(int index,int Left,int Right,int* a) {
        tree[index].left=Left;
        tree[index].right=Right;
        if(Left==Right) { //leaf
            tree[index].sum=a[Left];
            tree[index].leftmax=tree[index].rightmax=tree[index].summax=a[Left];
            tree[index].leftmin=tree[index].rightmin=tree[index].summin=a[Left];
            return;
        }
        int mid=(Left+Right)/2;
        build(2*index,Left,mid,a);
        build(2*index+1,mid+1,Right,a);
        push_up(index);
    }
    void push_up(int index) { //Tag upload, merge subtree information
        tree[index].sum=tree[index*2].sum+tree[index*2+1].sum;
        tree[index].leftmax=max(tree[index*2].leftmax,tree[index*2].sum+tree[index*2+1].leftmax); //leftmaxYou can come from your left son. leftmax Or left->Right son leftmax
        tree[index].rightmax=max(tree[index*2+1].rightmax,tree[index*2+1].sum+tree[index*2].rightmax); //rightmaxEmpathy
        tree[index].summax=max(max(tree[index*2].summax,tree[index*2+1].summax),tree[index*2].rightmax+tree[index*2+1].leftmax); //summaxIt can come from individual sons. summax Or the middle part of the right and left sons
        tree[index].leftmin=min(tree[index*2].leftmin,tree[index*2].sum+tree[index*2+1].leftmin);
        tree[index].rightmin=min(tree[index*2+1].rightmin,tree[index*2+1].sum+tree[index*2].rightmin);
        tree[index].summin=min(min(tree[index*2].summin,tree[index*2+1].summin),tree[index*2].rightmin+tree[index*2+1].leftmin);
    }
    void modify(int index,int target,int data) {
        if(target<tree[index].left||target>tree[index].right)return; //Disjoint
        if(target==tree[index].left&&target==tree[index].right) {
            tree[index].sum=data;
            tree[index].leftmax=tree[index].rightmax=tree[index].summax=data;
            tree[index].leftmin=tree[index].rightmin=tree[index].summin=data;
            return;
        }
        modify(index*2,target,data);
        modify(index*2+1,target,data);
        push_up(index); //Mark uploading
    }
};
Segment_Tree st;
int n,m,a[100005];
int main() {
    n=Get_Int();
    for(int i=1; i<=n; i++)a[i]=Get_Int();
    st.build(1,1,n,a);
    m=Get_Int();
    for(int i=1; i<=m; i++) {
        int pos=Get_Int(),v=Get_Int();
        st.modify(1,pos,v);
        if(st.tree[1].summax==st.tree[1].sum)printf("%d\n",st.tree[1].sum-st.tree[1].summin); //Can't finish. 
        else printf("%d\n",max(st.tree[1].summax,st.tree[1].sum-st.tree[1].summin));
    }
    return 0;
}