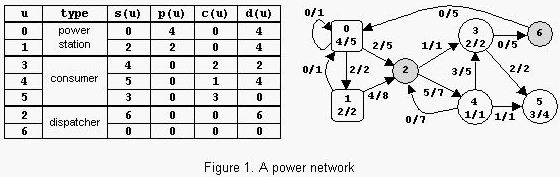
Description

A power network consists of nodes (power stations, consumers and
dispatchers) connected by power transport lines. A node u may be
supplied with an amount s(u) >= 0 of power, may produce an amount 0 <=
p(u) <= pmax(u) of power, may consume an amount 0 <= c(u) <=
min(s(u),cmax(u)) of power, and may deliver an amount
d(u)=s(u)+p(u)-c(u) of power. The following restrictions apply: c(u)=0
for any power station, p(u)=0 for any consumer, and p(u)=c(u)=0 for
any dispatcher. There is at most one power transport line (u,v) from a
node u to a node v in the net; it transports an amount 0 <= l(u,v) <=
lmax(u,v) of power delivered by u to v. Let Con=Σuc(u) be the power
consumed in the net. The problem is to compute the maximum value of
Con.

An example is in figure 1. The label x/y of power station u shows that
p(u)=x and pmax(u)=y. The label x/y of consumer u shows that c(u)=x
and cmax(u)=y. The label x/y of power transport line (u,v) shows that
l(u,v)=x and lmax(u,v)=y. The power consumed is Con=6. Notice that
there are other possible states of the network but the value of Con
cannot exceed 6.

Input

There are several data sets in the input. Each data set encodes a
power network. It starts with four integers: 0 <= n <= 100 (nodes), 0
<= np <= n (power stations), 0 <= nc <= n (consumers), and 0 <= m <=
n^2 (power transport lines). Follow m data triplets (u,v)z, where u
and v are node identifiers (starting from 0) and 0 <= z <= 1000 is the
value of lmax(u,v). Follow np doublets (u)z, where u is the identifier
of a power station and 0 <= z <= 10000 is the value of pmax(u). The
data set ends with nc doublets (u)z, where u is the identifier of a
consumer and 0 <= z <= 10000 is the value of cmax(u). All input
numbers are integers. Except the (u,v)z triplets and the (u)z
doublets, which do not contain white spaces, white spaces can occur
freely in input. Input data terminate with an end of file and are
correct.

Output

For each data set from the input, the program prints on the standard
output the maximum amount of power that can be consumed in the
corresponding network. Each result has an integral value and is
printed from the beginning of a separate line.

Sample Input

2 1 1 2 (0,1)20 (1,0)10 (0)15 (1)20
7 2 3 13 (0,0)1 (0,1)2 (0,2)5 (1,0)1 (1,2)8 (2,3)1 (2,4)7
         (3,5)2 (3,6)5 (4,2)7 (4,3)5 (4,5)1 (6,0)5
         (0)5 (1)2 (3)2 (4)1 (5)4

Sample Output

15
6

Hint

The sample input contains two data sets. The first data set encodes a
network with 2 nodes, power station 0 with pmax(0)=15 and consumer 1
with cmax(1)=20, and 2 power transport lines with lmax(0,1)=20 and
lmax(1,0)=10. The maximum value of Con is 15. The second data set
encodes the network from figure 1.

thinking

This question is about killing.

The idea of this problem is transformation. We build a super source point in front of the power station, connect each source point with an edge with the maximum load capacity, establish a super sink point behind the user, and connect each user with the super sink point with an edge with the maximum accepted capacity. And then it's the maximum flow.

Code

#include <cstdio>
#include <cstring>
#include <cctype>
#include <stdlib.h>
#include <string>
#include <map>
#include <iostream>
#include <stack>
#include <cmath>
#include <queue>
#include <vector>
#include <algorithm>
using namespace std;
typedef long long ll;
#define inf 0x3f3f3f3f
#define mem(a,b) memset(a,b,sizeof(a))
const int N=200+20;
int g[N][N],f[N][N],pre[N];//Respectively representing residual network, real flow network and precursor array
bool vis[N];//Tag array
int n,m;//Points and sides
bool bfs(int s,int t)
{
    mem(pre,-1);
    mem(vis,false);
    queue<int>q;
    vis[s]=true;
    q.push(s);
    while(!q.empty())
    {
        int now=q.front();
        q.pop();
        for(int i=0; i<=n; i++)
        {
            if(!vis[i]&&g[now][i]>0)
            {
                vis[i]=true;
                pre[i]=now;
                if(i==t)
                    return true;
                q.push(i);
            }
        }
    }
    return false;
}
int EK(int s,int t)
{
    int v,w,d,maxflow=0;
    while(bfs(s,t))
    {
        v=t;
        d=inf;
        while(v!=s)
        {
            w=pre[v];
            d=min(d,g[w][v]);
            v=w;
        }
        maxflow+=d;
        v=t;
        while(v!=s)
        {
            w=pre[v];
            g[w][v]-=d;
            g[v][w]+=d;
            if(f[v][w]>0)
                f[v][w]-=d;
            else
                f[w][v]+=d;
            v=w;
        }
    }
    return maxflow;
}
int main()
{
    int np,nc,a,b,c;
    while(~scanf("%d%d%d%d",&n,&np,&nc,&m))
    {
        mem(g,0);
        while(m--)
        {
            while(getchar()!='(');
            scanf("%d,%d)%d",&a,&b,&c);
            g[a+1][b+1]+=c;
        }
        while(np--)
        {
            while(getchar()!='(');
            scanf("%d)%d",&a,&c);
            g[0][a+1]+=c;
        }
        while(nc--)
        {
            while(getchar()!='(');
            scanf("%d)%d",&a,&c);
            g[a+1][n+1]+=c;
        }
        n++;
        printf("%d\n",EK(0,n));
    }
    return 0;
}