(1) POJ1050 - classical maximum segments and problems

POJ1050
Title: find the maximum sum of submatrixes of a given matrix, n ≤ 100n ≤ 100n ≤ 100
Solution idea: because n is very small, it can be done by O (N3) O (N3) O (N3). Enumerate the upper and lower bounds of the matrix, and deal with the sum of each column under the current upper and lower bounds. According to the classic idea: scan the sum of each column, and continuously add sub segments. When the sum of sub segments becomes negative, clear the current whole sub segment, and then add it again, and constantly update the answer.
ac Code:

#include <iostream>
#include <cstring>
#include <stdlib.h>
#include <climits>
using namespace std;
typedef long long ll;
const int maxn = 110;
int a[maxn][maxn], c[maxn], s[maxn];
int n, ans = INT_MIN;
int main()
{
    //freopen("/Users/zhangkanqi/Desktop/11.txt","r",stdin);
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
            scanf("%d", &a[i][j]);
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= n; j++)//Enumerate the beginning and end row numbers of submatrix, and find the column values in the current i~j rows
        {
            memset(c, 0, sizeof(c));
            memset(s, 0, sizeof(s));
            for(int k = 1; k <= n; k++)
                for(int p = i; p <= j; p++)
                    c[k]+=a[p][k];
            //Clear when sub segment sum becomes negative, otherwise continue to join
            for(int k = 1; k <= n; k++)
            {
                s[k] = s[k-1]>0 ? s[k-1]+c[k] : c[k];
                ans = max(ans, s[k]);
            }

        }
    }
    printf("%d\n", ans);
    return 0;
}

(2)POJ2018 - Maximum sub segment and with length not less than F

POJ2018
Title: N(1 ≤ N ≤ 1e5)N(1 ≤ N ≤ 1e5)N(1 ≤ N ≤ 1e5)N(1 ≤ N ≤ 1e5) farms, each farm has cowscowscows head, select several consecutive farms, to meet the number of farms ≥ f ≥ f ≥ F, and the average value of cattle in these farms is the largest, and get the maximum value.
Solution: two answers. Subsegments and can be converted to:
max⁡i−j≥F{Aj+1+Aj+2+...+Ai}=max⁡F≤i≤n{sumi−min⁡0≤j≤i−F{sumj}}\max \limits_{i-j≥F}\{A_{j+1}+A_{j+2}+...+A_i\}=\max\limits_{F≤i≤n}\{sum_i-\min\limits_{0≤j≤i-F}\{sum_j\}\}i−j≥Fmax​{Aj+1​+Aj+2​+...+Ai​}=F≤i≤nmax​{sumi​−0≤j≤i−Fmin​{sumj​}}
With the increase of i, the value range of j only increases by 1 at a time, which is equivalent to that min {sumj} \ min \ {sum} min {sumj} will only add a new value at a time, so the sub segment length can be handled within O(n)O(n)O(n) O (n) O (n), which is not less than the maximum sub segment sum of F.
If the current dichotomy answer is x x x, then the sum of sigma and − length L*x=p=0\sum and - length L*x=p=0 Σ and - length L*x=p=0 Σ and − length L*x=p=0 are obtained from the sum of sigma and length L=x\frac{\sum and} {length L}=x Length L Σ and = length L*x=p=0, (equivalent to the sum of the largest subsections of each cow − x cows xcows − x). If P > = 0P > = 0P > = 0, you can continue to expand the answer, otherwise you can narrow the answer.
ac Code:

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e5+10;
const double eps = 1e-5;
int n, f;//At least f fields
double a[maxn], sum[maxn], b[maxn];
int main()
{
    //freopen("/Users/zhangkanqi/Desktop/11.txt","r",stdin);
    scanf("%d %d", &n, &f);
    for(int i = 1; i <= n; i++)
        scanf("%lf", &a[i]);
    double l = 0, r = 1e6;
    while(r-l>eps)
    {
        double mid = (l+r)/2;
        for(int i = 1; i <= n; i++)
        {
            b[i] = a[i]-mid;
            sum[i] = sum[i-1]+b[i];
        }
        double MAX = -1e10;//Maximum continuous subsegment sum with length > = f
        double MIN = 1e10;
        for(int i = f; i <= n; i++)
        {
            MIN = min(MIN, sum[i-f]);
            MAX = max(MAX, sum[i]-MIN);
        }
        if(MAX>=0) l = mid;
        else r = mid;
    }
    printf("%d\n", (int)(r*1000));
    return 0;
}

(3)HDOJ6638 line segment tree maintenance maximum sub segment and

HDOJ6638
Topic: given the coordinates (x,y)(x,y)(x,y) and weights (www) of nnn points, find the sum of the weights of the maximum submatrix. −1e9≤x,y,w≤1e9,∑n≤10000-1e9≤x,y,w≤1e9,\sum{n}≤10000−1e9≤x,y,w≤1e9,∑n≤10000.
Solution idea: n n n is relatively large, so it can't be enumerated by O (N3) O (N3) O (N3) O (N3) O (N3) violence. We need to change two-dimensional to one-dimensional, O(n2logn) to solve it. O(n^2logn). O(n2logn). Discretize all yyys, change the yyy value of the points to rankyrankyranky, and then sort all the points according to xxx from small to large. The order of the points processed in this way is as follows: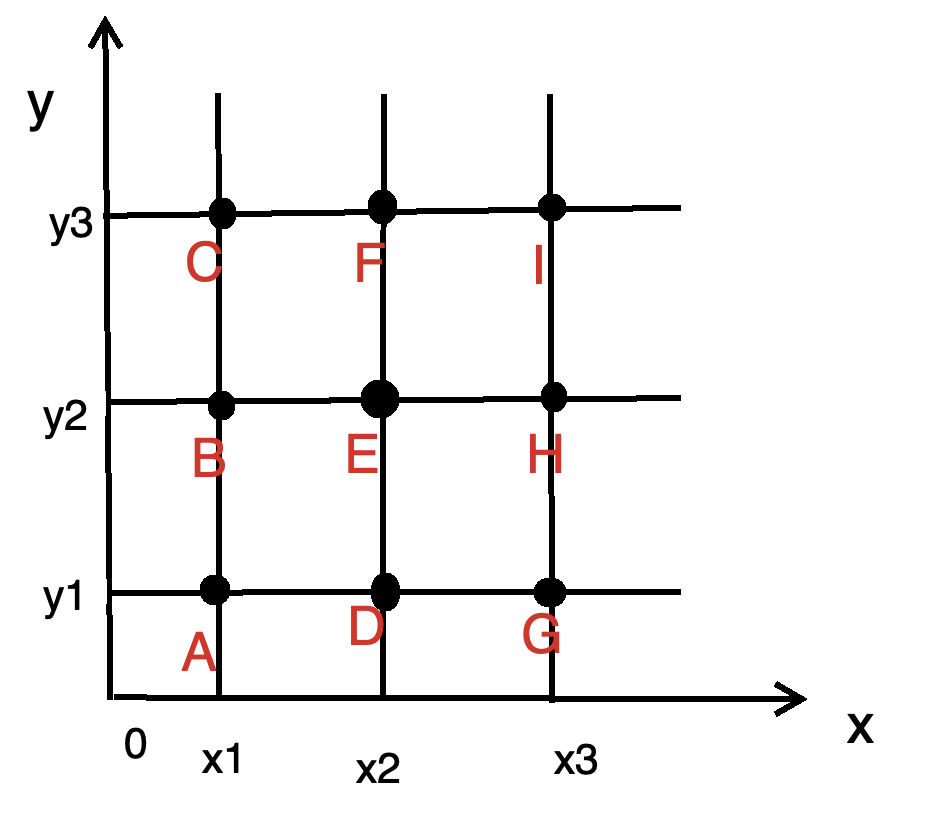

In this paper, the author analyzes the characteristics of , h, I}.
ac Code:

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 2e3+10;
struct point{
    int x, y, w;
    point(){};
    friend bool operator < (point a, point b)
    {
        return a.x==b.x ? a.y<b.y : a.x<b.x;
    }
}p[maxn];
struct node{
    int l, r;
    ll mx, max_pre, max_suf, sum;//Interval maximum subsegment sum, maximum prefix sum, maximum suffix sum, sum
}tree[maxn<<2];
int y[maxn];
int t, n;
void build(int id, int l, int r)
{
    tree[id].l = l; tree[id].r = r;
    tree[id].sum=tree[id].max_pre=tree[id].max_suf=tree[id].mx=0;
    if(l==r) return ;
    int mid = (l+r)>>1;
    build(id<<1, l, mid);
    build(id<<1|1, mid+1, r);
}
void push_up(int id)
{
    tree[id].sum = tree[id<<1].sum+tree[id<<1|1].sum;
    tree[id].max_pre = max(tree[id<<1].max_pre, tree[id<<1].sum+tree[id<<1|1].max_pre);
    tree[id].max_suf = max(tree[id<<1|1].max_suf, tree[id<<1|1].sum+tree[id<<1].max_suf);
    //Maximum subsegment and mx = max (left interval mx, right interval mx, left interval maximum suffix and + right interval maximum prefix sum)
    tree[id].mx = max(max(tree[id<<1].mx, tree[id<<1|1].mx), tree[id<<1].max_suf+tree[id<<1|1].max_pre);
}
void insert(int id, int k, int w)//From id=1, rank y as k leaf node + w
{
    if(tree[id].l==tree[id].r)
    {
        tree[id].sum=tree[id].max_pre=tree[id].max_suf=tree[id].mx=tree[id].mx+w;
        return ;
    }
    int mid = (tree[id].l+tree[id].r)>>1;
    if(k<=mid) insert(id<<1, k, w);
    else insert(id<<1|1, k, w);
    push_up(id);
}

int main()
{
    //freopen("/Users/zhangkanqi/Desktop/11.txt","r",stdin);
    scanf("%d", &t);
    while(t--)
    {
        ll ans = LONG_LONG_MIN;
        scanf("%d", &n);
        for(int i = 1; i <= n; i++)
        {
            scanf("%d %d %d", &p[i].x, &p[i].y, &p[i].w);
            y[i] = p[i].y;
        }
        sort(y+1, y+1+n);
        int num = unique(y+1, y+1+n)-(y+1);
        for(int i = 1; i <= n; i++)
            p[i].y=lower_bound(y+1, y+1+num, p[i].y)-y;
        sort(p+1, p+1+n);//After y discretization, it is sorted by x from small to large
        for(int i = 1; i <= n; i++)
        {
            if(i!=1 && p[i].x==p[i-1].x) continue;//Do not build duplicate trees
            build(1, 1, num);
            for(int j = i; j <= n; j++)
            {
                if(j!=i && p[j].x!=p[j-1].x) ans = max(ans, tree[1].mx);
                insert(1, p[j].y, p[j].w);
            }
            ans = max(ans, tree[1].mx);
        }
        printf("%lld\n", ans);
    }
    return 0;
}