Before you look at this topic, you can review the decomposition of strong interconnection component by POJ2186.

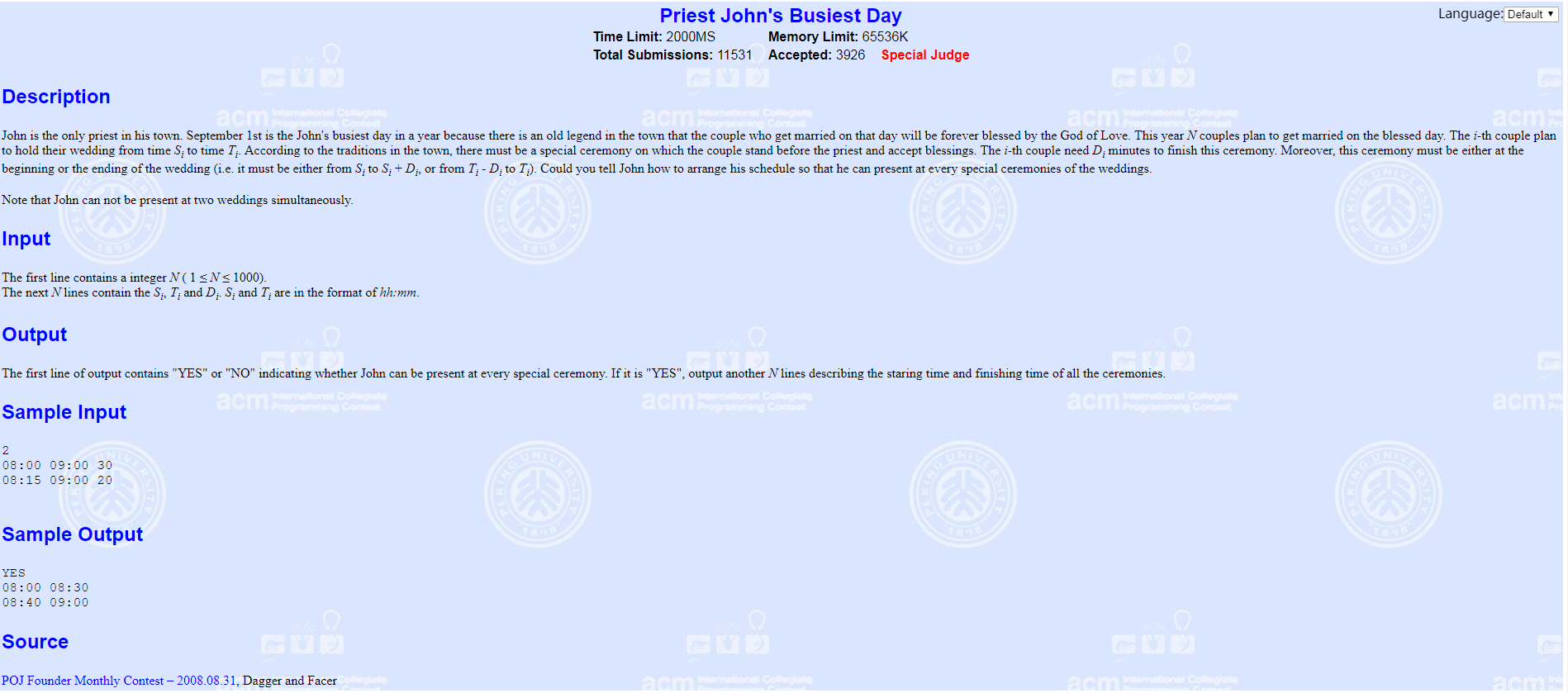
Topic: Give N triples of start time and end time and duration, duration can be after the start or before the end, ask how to allocate it without conflict.

I am the dividing line.

First, explain the conjunctive paradigm (discrete mathematics has been taught):
If the number of words in each sentence in the conjunctive paradigm does not exceed two, it is called the 2-SAT problem.
Generally called n-SAT problem

Take a chestnut: (a_b)a(a_b)a when a is false and B is true.

By using the knowledge of strongly connected components, the 2-SAT problem can be solved in the linear time of the number of Boolean formula sentences. We have learned the implication paradigm in discrete mathematics. For a B a b, it can be converted to (a b) (B a) (a b) (B a)

The following is the drawing process:
For each Boolean variable x, two vertices X and x_x are constructed, and directed graphs are constructed for directed edges.
In a digraph, if a can reach b, then a is true and B is true.
Therefore, the Boolean values of all words in the same strongly connected component are the same.
Especially, if x and x_x_are both in the same strongly connected component, it is obvious that this strongly connected component can never be true.
On the contrary, if there is no such Boolean variable, for each Boolean variable x, let

The topological order of the strongly connected component where x is located is after the strongly connected component where x is located (that is, to compare the topological order of the two).

That is to say, the value of the formula is the solution of a set of suitable Boolean variables.

I am the dividing line.

For each triple, only two choices are made after the start and before the end. Let's set the variable xi.
xi is true <-> start inserting length after start

With these theoretical supports, there are four combinations for each triple:
Start - start
Start and end
End - start
End - end
(There is no end-start in the example in this question)
If the conflict starts - starts, then the value of x1 x2 x1 X2 is true.
So the conjugate paradigm is (x1 x2)(x1 x2)(x1 x2)(x1 x2)(x1 x2)(x1 x2)(x1 x2)(x1 x2)
When the value of x1 is true and the value of x2 is false, the value is true.
The next step is to decompose the strongly connected components and determine whether there is a set of Boolean variables that make the Boolean formula true.
(Here we use the theorem with the previous one: if the topological order of the strongly connected component where x is located is after x, then x is true after x, then x is true

#include <iostream>
#include <map>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <vector>
#include <queue>
#include <stack>
#include <functional>
#include <set>
#include <cmath>
using namespace std;
#define IOS std::ios::sync_with_stdio (false);std::cin.tie(0)
#define pb push_back
#define PB pop_back
#define bk back()
#define fs first
#define se second
#define sq(x) (x)*(x)
#define eps (3e-7)
#define IINF (1<<29)
#define LINF (1ll<<59)
#define INF (1000000000)
#define FINF (1e3)
#define clr(x) memset((x),0,sizeof (x));
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
typedef pair<int,int> P;

const int maxn=2005;
int n;
int a[maxn][3];
char r[300];
vector<int> G[maxn],rG[maxn],od;
bool vis[maxn];
int sccid[maxn];
int get(char a,char b){
    return (a-'0')*10+b-'0';
}
bool inter(int a,int b,int c,int d){
    return !(a>=d||b<=c);
}
void addedge(int a,int b){
    G[a].pb(b);
    rG[b].pb(a);
}
void dfs1(int v){
    vis[v]=1;
    for(int i=0;i<G[v].size();i++){
        int u=G[v][i];
        if(!vis[u]) dfs1(u);
    }
    od.pb(v);
}
void dfs2(int v,int k){
    vis[v]=1;
    sccid[v]=k;
    for(int i=0;i<rG[v].size();i++){
        int u=rG[v][i];
        if(!vis[u]) dfs2(u,k);
    }
}
int V;
void scc(){
    clr(vis);od.clear();
    for(int i=1;i<=V;i++){
        if(!vis[i]) dfs1(i);
    }
    clr(vis);
    int id=1;
    for(int i=od.size()-1;i>=0;i--){
        int v=od[i];
        if(!vis[v]) dfs2(v,id++);
    }
}
void build(){
    for(int i=1;i<=n;i++){
        for(int j=i+1;j<=n;j++){
            if(inter(a[i][0],a[i][0]+a[i][2],a[j][0],a[j][0]+a[j][2])){
                addedge(i,j+n);
                addedge(j,i+n);
            }
            if(inter(a[i][0],a[i][0]+a[i][2],a[j][1]-a[j][2],a[j][1])){
                addedge(i,j);
                addedge(j+n,i+n);
            }
            if(inter(a[i][1]-a[i][2],a[i][1],a[j][0],a[j][0]+a[j][2])){
                addedge(i+n,j+n);
                addedge(j,i);
            }
            if(inter(a[i][1]-a[i][2],a[i][1],a[j][1]-a[j][2],a[j][1])){
                addedge(i+n,j);
                addedge(j+n,i);
            }
        }
    }
}
bool ans[maxn];
int main(){
    freopen("/home/slyfc/CppFiles/in","r",stdin);
    //freopen("defense.in","r",stdin);
    //freopen("defense.out","w",stdout);
    cin>>n;
    V=n*2;
    for(int i=1;i<=n;i++){
        scanf("%s",r);
        a[i][0]=get(r[0],r[1])*60+get(r[3],r[4]);
        scanf("%s",r);
        a[i][1]=get(r[0],r[1])*60+get(r[3],r[4]);
        scanf("%d",&a[i][2]);
    }
    build();
    scc();
    for(int i=1;i<=n;i++){
        if(sccid[i]==sccid[i+n]){
            puts("NO");
            return 0;
        }else{
            if(sccid[i]>sccid[i+n]){
                ans[i]=1;
            }else{
                ans[i]=0;
            }
        }
    }
    puts("YES");
    for(int i=1;i<=n;i++){
        if(ans[i]){
            int s=a[i][0],t=a[i][0]+a[i][2];
            printf("%02d:%02d %02d:%02d\n",s/60,s%60,t/60,t%60);
        }else{
            int s=a[i][1]-a[i][2],t=a[i][1];
            printf("%02d:%02d %02d:%02d\n",s/60,s%60,t/60,t%60);
        }
    }
    return 0;
}