Command generals plan to deploy their artillery units on the NM grid map. A NM map consists of N rows and M columns. Each grid of the map may be mountain (represented by "H") or plain (represented by "P"), as shown below. At most one artillery unit can be deployed on each plain terrain (artillery units cannot be deployed on mountainous areas); the attack range of an artillery unit on the map is shown in the black area in the figure.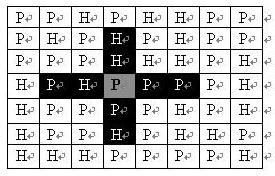

If an artillery unit is deployed on the gray-marked plain in the map, the black grid in the map represents the area it can attack: two squares left and right along the horizontal direction and two squares up and down along the vertical direction. No other white grids on the graph can be attacked. It can be seen from the map that the artillery's attack range is not affected by the terrain.
Now, the generals plan how to deploy artillery units, on the premise of preventing accidental injuries (to ensure that no two artillery units can attack each other, that is, no artillery unit is within the scope of attack by other artillery units), and how many artillery units of our army can be placed in the whole map area at most.
Input
The first line contains two positive integers separated by spaces, representing N and M, respectively.
Next in line N, each line contains consecutive M characters ('P'or'H'), with no spaces in it. Represents the data of each row in the map in sequence. N <= 100; M <== 10.
Output
A single line, containing an integer K, indicates the maximum number of artillery units that can be placed.
Sample Input
5 4
PHPP
PPHH
PPPP
PHPP
PHHP
Sample Output
6

Idea: It's similar to the topic of that farm. But dpdpdp here needs to be defined as three-dimensional.

• dp[i][j][k]dp[i][j][k]dp[i][j][k] DP [i] [j] [k] denotes the maximum number of artillery in line iii in the state of jjj and kkk in the previous line
• dp[i][j][k]=max(dp[i_1] [k] [x]) +NumOne of (j) DP [i] [j] [k] [k] = max (dp [i-1] [k] [x]) + NumOne of (j) DP [i] [j] [k] [x] = max (dp [i_1] [k] [x] + NumOne of (j), where XX is the legal state of kkk, JJ
• And 1< = m< = 101< = m< = 101 <= m <== 10, the range of jjj and kkk can be 1024, so here is an optimization, preprocessing all the legal states of rows in advance, and extracting them directly from these States every time. Up to 60 solutions
• Space can also be optimized. Since all the legal states are processed, the latter two dimensions of the DPDP array can be represented directly by the subscript of the legal state. With rolling array, the spatial complexity is O(2_602)O(2 * 60^2)O(2 602) O(2 602), and the time complexity is O(n 603)O(n * 60^3)O(n 603).

Code:

#include<cstdio>
#include<algorithm>
#include<vector>
#include<iostream>
#define debug(x) cout << "[" << #x <<": " << (x) <<"]"<< endl
#define pii pair<int,int>
#define clr(a,b) memset((a),b,sizeof(a))
#define rep(i,a,b) for(int i = a;i < b;i ++)
#define pb push_back
#define MP make_pair
#define LL long long
#define ull unsigned LL
#define ls i << 1
#define rs (i << 1) + 1
#define fi first
#define se second
#define ptch putchar
#define CLR(a) while(!(a).empty()) a.pop()

using namespace std;

bool isdigit(char ch){
    return ch >= '0' && ch <= '9';
}

inline LL read() {
    LL s = 0,w = 1;
    char ch = getchar();
    while(!isdigit(ch)) {
        if(ch == '-') w = -1;
        ch = getchar();
    }
    while(isdigit(ch))
        s = s * 10 + ch - '0',ch = getchar();
    return s * w;
}
inline void write(LL x) {
    if(x < 0)
        putchar('-'), x = -x;
    if(x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}

const int maxn = 70;
vector<int> may;
char mp[110][maxn];
int dp[3][maxn][maxn];        /// i line j state. i - 1 line k state
int n,m;

int state(int i){
    int tmp = 1;
    int s = 0;
    for(int j = m;j >= 1;-- j){
        s += tmp * (mp[i][j] == 'H');
        tmp *= 2;
    }
    return s;
}

int main() {
//#ifndef ONLINE_JUDGE
//    freopen("in.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
//#endif
    n = read(),m = read();
    for(int i = 1;i <= n;++ i) scanf("%s",mp[i] + 1);
    int k = 1 << m;
    int cnt = 0,sta = state(1);
    for(int i = 0;i < k;++ i){
        if((i & (i << 1)) || (i & (i << 2)))
            continue;
        may.pb(i);
        if(!(sta & i))
            dp[1][cnt][0] = __builtin_popcount(i);
        cnt ++;
    }
    sta = state(2);
    for(int i = 0;i < may.size();++ i){///i
        if(may[i] & sta) continue;
        for(int j = 0;j < may.size();++ j){///i-1
            if(may[i] & may[j]) continue;
            dp[0][i][j] = max(dp[0][i][j],dp[1][j][0] + __builtin_popcount(may[i]));
        }
    }
    for(int i = 3;i <= n;++ i){
        sta = state(i);
        for(int j = 0;j < may.size();++ j){ ///i
            if(may[j] & sta) continue;
            for(int k = 0;k < may.size();++ k){///i-1
                if(may[j] & may[k]) continue;
                for(int l = 0;l < may.size();++ l){///i-2
                    if(may[k] & may[l]) continue;
                    if(may[j] & may[l]) continue;
                    dp[i % 2][j][k] = max(dp[i % 2][j][k],dp[(i % 2) ^ 1][k][l] + __builtin_popcount(may[j]));
                }
            }
        }
    }
    int maxx = 0;
    for(int i = 0;i < may.size();++ i)
        for(int j = 0;j < may.size();++ j)
            maxx = max(maxx,dp[n % 2][i][j]);
    write(maxx);
    return 0;
}