This article is for reference only. Thank you

Problem Description:

Simple algorithm (non dynamic programming):

#include <stdio.h>
#define max 1000

typedef struct {
    int N;
    int Money[max];
    int solution[max];
}System;

System create(){
    System A;
    for (int i=0; i<max; i++) {
        A.Money[i]=0;
        A.solution[i]=0;
    }
    
    scanf("%d",&A.N);
    for (int i=1; i<=A.N; i++) {
        scanf("%d",&A.Money[i]);
    }
    A.solution[0]=1;
    return A;
}

double workout(System A,int M){
    double evaluate=0;
    
    for (int money=1; money<=M; money++) {
        int sum=0,c=money;
        for (int i=1; i<=A.N; i++) {
            sum+=c/A.Money[i];
            c%=A.Money[i];
        }
        A.solution[money]=sum;
    }
    
    for (int i=1; i<=M; i++) {
        evaluate+=A.solution[i];
    }
    
    return evaluate/M;
}

int main(int argc, const char * argv[]) {
    int M=0;
    double VB=0,VL=0;
    System B,L;
    scanf("%d",&M);
    B=create();
    L=create();
    
    VB=workout(B, M);
    VL=workout(L, M);
    
//    printf("%.2f\t",VB);
//    printf("%.2f\t",VL);
    
    if (VB<VL) {
        printf("B\n");
    } else if (VB>VL) {
        printf("L\n");
    }else {
        printf("=\n");
    }
    return 0;
}

Using dynamic programming after optimization -- knapsack problem (complete knapsack?) Algorithm:

This part of the code can be written again if free

Problem evolution:

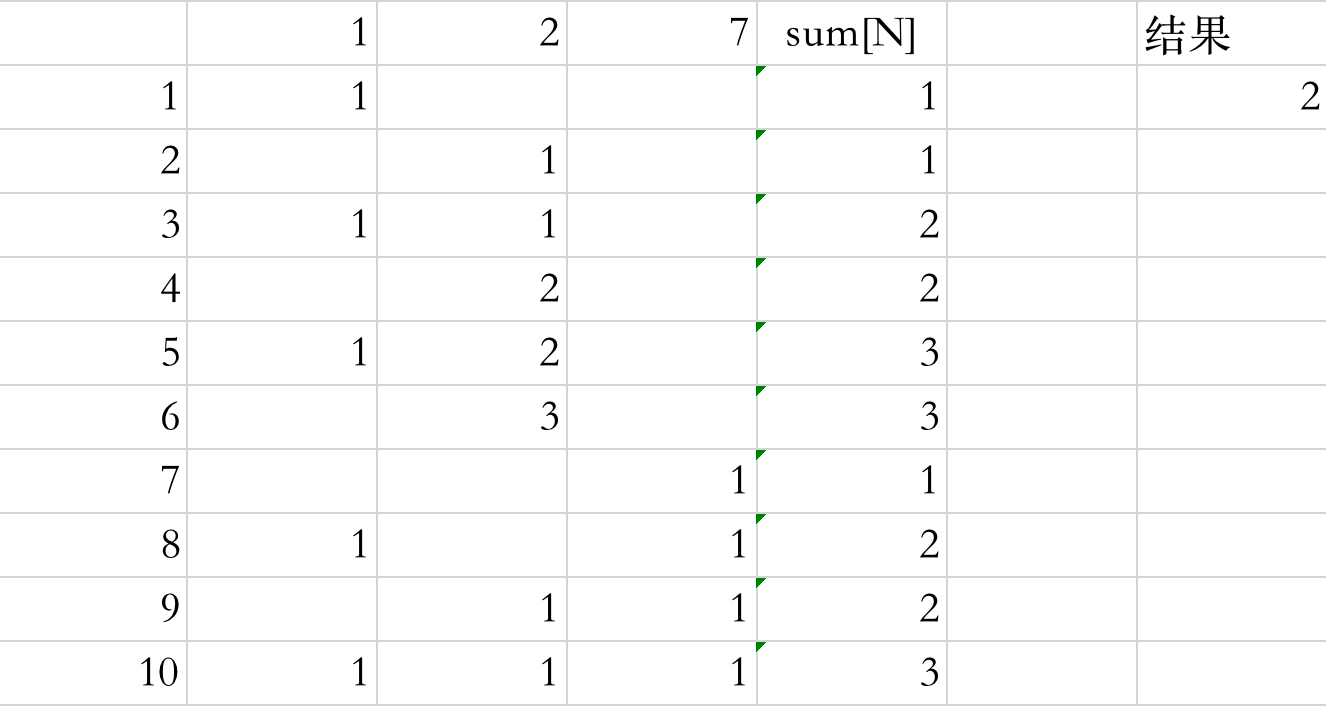
To find the sum of the number of schemes (complete knapsack problem) of each gold coin quota between 1 and M composed of N currencies (similar to the monetary system of a bank):

• Thought analysis:

From the meaning of the question, we can see that we need to get the number of (Money[N]) schemes where all numbers from 1 to M are composed of N numbers. First of all, we can simplify the problem into a solution
1. When there is only one currency, how many different collocation schemes can each value from 1 to M have and store the records in a one-dimensional array for dynamic planning
2. Based on the existing one-dimensional array data, add another currency, and find out the different matching schemes that the two currencies can provide for 1 to M together
With the new combination scheme, we can get the different combination schemes that these two currencies can form
3. By analogy, we can get the total number of collocation schemes that N currencies can form
It should be noted that each denomination of a currency can at least constitute its own denomination

• Algorithm description:

1. It is necessary to declare that a structure is used to store two different currency systems from tribes and alliances. It needs to include the number of types of currency denominations N, and one-dimensional array Money and
It is used to record different matching schemes that have been formed
2. A create function is needed to establish and input the data of the currency system, and initialize all data before input
3. When calculating different collocation schemes, it is necessary to calculate the collocation scheme composed of one currency and two currencies at different levels, etc
When calculating the face value of current n currencies, the collocation scheme of 1 to M data = all existing collocation schemes starting from the nth face value + (n-the collocation scheme with the amount of the value before d) existing
4. Average the number of all allocation schemes on 1 to M that have been dynamically planned and stored, and then compare the average value of tribe and alliance to get the smaller one

• Test data:

10
3 7 2 1
3 8 3 1

• Test results:

B

#include <stdio.h>
#define max 1000

typedef struct {
    int N;
    int Money[max];
    int solution[max];
}System;

System create(){
    System A;
    for (int i=0; i<max; i++) {
        A.Money[i]=0;
        A.solution[i]=0;
    }
    
    scanf("%d",&A.N);
    for (int i=1; i<=A.N; i++) {
        scanf("%d",&A.Money[i]);
    }
    A.solution[0]=1;
    return A;
}

int workout(System A,int M){
    int evaluate=0;
    
    //First calculate the collocation scheme when there is only Money[1], then calculate the collocation scheme composed of Money[1] and Money[2], and so on to calculate the collocation scheme of N currencies
    for (int i=1; i<=A.N; i++) {
        for (int j=A.Money[i]; j<=M; j++) {
            A.solution[j]=A.solution[j]+A.solution[j-A.Money[i]];
        }
    }
    
    for (int i=1; i<=M; i++) {
        evaluate+=A.solution[i];
    }
    
    return evaluate/M;
}

int main(int argc, const char * argv[]) {
    int M=0,VA=0,VB=0;
    System A,B;
    scanf("%d",&M);
    A=create();
    B=create();
    
    VA=workout(A, M);
    VB=workout(B, M);
    
//    printf("%d\t",VB);
//    printf("%d\t",VA);
    if (VA<VB) {
        printf("A\n");
    } else {
        printf("B\n");
    }
    return 0;
}