1060. Are They Equal (25)

If a machine can save only 3 significant digits, the float numbers 12300 and 
12358.9 are considered equal since they are both saved as 0.123*105 with simple chopping. Now 
given the number of significant digits on a machine and two float numbers, you are supposed to 
tell if they are treated equal in that machine.

Input Specification:

Each input file contains one test case which gives three numbers N, A and B, where N (<100) is 
the number of significant digits, and A and B are the two float numbers to be compared. Each 
float number is non-negative, no greater than 10100, and that its total digit number is less than 100.

Output Specification:

For each test case, print in a line "YES" if the two numbers are treated equal, and then the 
number in the standard form "0.d1...dN*10^k" (d1>0 unless the number is 0); or "NO" if they are 
not treated equal, and then the two numbers in their standard form. All the terms must be 
separated by a space, with no extra space at the end of a line.

Note: Simple chopping is assumed without rounding.

Sample Input 1:
3 12300 12358.9
Sample Output 1:
YES 0.123*10^5
Sample Input 2:
3 120 128
Sample Output 2:
NO 0.120*10^3 0.128*10^3

• Analysis: There is no arithmetic in this way. It's just simulation. We should pay attention to all kinds of situations.

  • Solution: Scientific representation consists of two parts: base number and index. Comparing the size of two numbers is to compare the size of these two factors. Comparing the index, we only need to calculate the width of the data, which is determined by the position of the point and the non-zero position difference. The bottom number, the zero of the head and the middle number are removed. Such numbers are finally used to compare the bottom number.
    (At first, I thought it was a simple question, so instead of obviously making two parts of scientific number, I made a direct comparison and skipped it in comparison. Finally, there were a lot of loopholes and the code was confused.)
  • Simulated data:

  3 12300 12358.9
  YES 0.123*10^5
  
  1 12300 12358.9
  YES 0.1*10^5
  
  1 1.2300 1.23589
  YES 0.1*10^1
  
  5 1.2300 1.23589
  NO 0.12300*10^1 0.12358*10^1
  
  4 0.01234 0.012345
  YES 0.1234*10^-1
  
  5 0.01234 0.012345
  NO 0.12340*10^-1 0.12345*10^-1
  
  5 0.1234 0.12345
  NO 0.12340*10^0 0.12345*10^0
  
  0 0.11 0
  YES 0.*10^0perhaps YES 0.0*10^0，Fine AC，The test point should not have this example
  
  1 0.1 0
  NO 0.1*10^0 0.0*10^0
  
  1 0.0 0.1
  NO 0.0*10^0 0.1*10^0
  
  1 0.0 0.000
  YES 0.0*10^0
  
  1 00.0 0.000
  YES 0.0*10^0
  
  4 00.0 0.000
  YES 0.0000*10^0
  
  5 00.0 0.000
  YES 0.00000*10^0
  
  1 05.0 5.000
  YES 0.5*10^1
  
  1 00.01 0.010
  YES 0.1*10^-1
  //Be careful:1 0 0
  

• code:

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
//Calculate the data width, where ma is the decimal point and mb is the first non-zero number
int width(char*c,int n,int &ma,int &mb)
{
  //deal with 0.000123
  int a=n;
  int b=-1;
  for(int i=0;i<n;i++)
  {
    if(a!=n&&b>=0)
      break;
    if(a==n&&c[i]=='.')//Decimal point position
      a=i;
    else if(b==-1&&c[i]!='0')//First non-zero position
      b=i;
  }
  ma=a; mb=b;
  //If no non-zero digits are found, the width of the data is 0.
  if(b==-1)
  {
    mb=0;
    return 0;
  }
  if(a>b)
    return a-b;
  else
    return a-b+1;
}
int main()
{
//  freopen("in","r",stdin);
  int n;
  const int MAX=2000;
  char c[MAX];
  char a[MAX];
  char b[MAX];
  fill_n(a,MAX,'0');
  fill_n(b,MAX,'0');
  scanf("%d %s",&n,c);
  int aa,ab,ba,bb;
  int ma=width(c,strlen(c),aa,ab);
  int i=ab;
  int j=0;
  //The first non-zero digit will be copied into a to facilitate the formatting of data output.
  for(;i<strlen(c);i++,j++)
  {
    if(c[i]=='.')
    {
      j--;
      continue;
    }
    a[j]=c[i];
  }
  //  a[j]='A [j]='\ 0''; //View data in a
  scanf("%s",c);
  int mb=width(c,strlen(c),ba,bb);
  //Copy numbers from the first non-zero number to b to facilitate formatting data output
  for(i=bb,j=0;i<strlen(c);i++,j++)
  {
    if(c[i]=='.')
    {
      j--;
      continue;
    }
    b[j]=c[i];
  }
  // b[j]='\0';


  int flag=1;
  //Comparing the data expressed by two scientific counting methods, comparing whether the base number is the same when the width and width of the data are equal.
  //N is big enough.
  if(ma!=mb)
    flag=0;
  else
    for(int i=0;i<n;i++)
    {
      if(a[i]!=b[i])
      {
        flag=0;
        break;
      }
    }

  if(flag==1)
    printf("YES");
  else
    printf("NO");
  //Attention should be paid to making up 0 when the base width is less than the accuracy.
  printf(" 0.");
  for(int i=0;i<n;i++)
  {
      printf("%c",a[i]);
  }
  printf("*10^%d",ma);

  if(flag==0)
  {
      printf(" 0.");
      for(int i=0;i<n;i++)
          printf("%c",b[i]);
      printf("*10^%d",mb);
  }
  printf("\n");
  return 0;
}

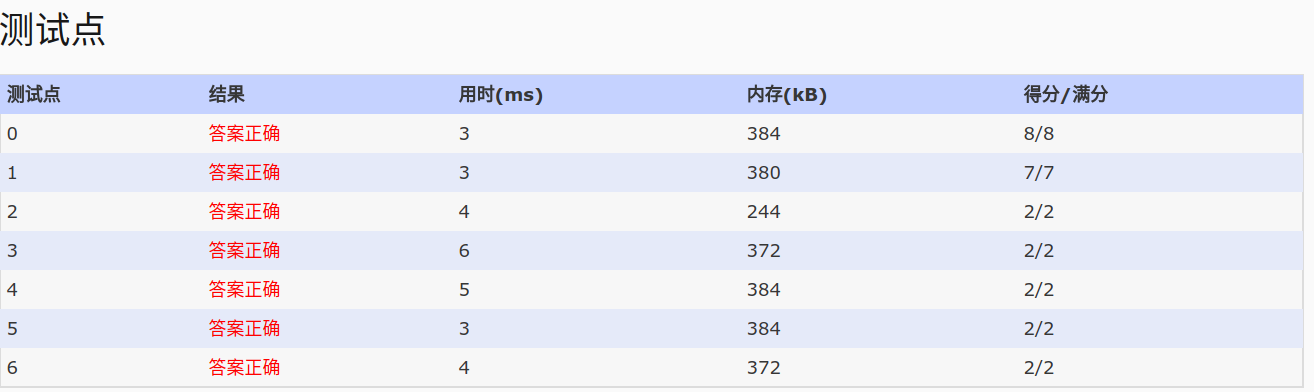
• AC: