subject

"Correct answer" is the most gratifying reply given by the automatic question judgment system. This question belongs to PAT's "correct answer" distribution - as long as the read string meets the following conditions, the system will output "correct answer", otherwise it will output "wrong answer".

The conditions for getting "correct answer" are:

1. There must be only   P,   A,   T these three characters cannot contain other characters;
2. Arbitrary shape such as   xPATx   All strings can get "correct answer", where   x   Either an empty string, or just letters   A   String composed of;
3. If   aPbTc   Is correct, then   aPbATca   It is also true that   a,   b,   c   Are either empty strings or are composed of only letters   A   A string consisting of.

Now please write an automatic referee program for PAT to determine which strings can get the "correct answer".

Input format:

Each test input contains 1 test case. Line 1 gives a positive integer   n   (≤ 10), is the number of strings to be detected. Next, each string occupies one line. The length of the string does not exceed 100 and does not contain spaces.

Output format:

The detection result of each string occupies one line. If the string can get "correct answer", it will be output   YES, otherwise output   NO.

First analyze the three conditions

1: It contains three characters of PAT, and there can be no other SDAD, etc

2: In other words, PAT, APATA, AAAPATAAA and n*APATn*A are all correct

3: Both aPbTc and aPbATca are correct. Let's see if PT is segmented

That is, aP b Tc ~~aP bA Tca is actually equivalent

Because this is a string, so look at the last c and ca and think about whether there may be a multiple relationship

Then a, b and c are either empty or n*A

Combined with the correct answer of the example

The front of P is called segment a, the middle of PT is called segment b, and the back of T is called segment c

That is, the n*A represented by the length of segment b multiplied by segment a should be equal to the following segment c

That is:

c = len(b)*a 

We can use this inference for data matching, so regularization is the best method

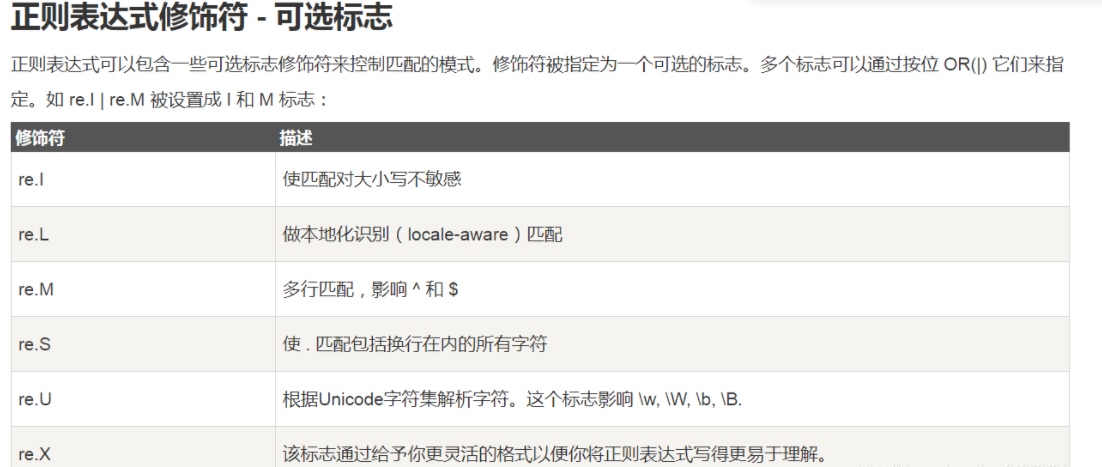
Definition of regular:

Here you need to use:

*Represents 0 or infinite extensions of the previous character

+One or infinite extension of the previous character

The matching rule is A*PA+TA*

.Represents any single character
[ ] Character set, which gives the value range of a single character [abc]express a,b,c [a-z]express a reach z All single characters of

[^] A non character set that gives an exclusion range for a single character [^abc]Indicates non a or b or c Single character of

* Zero or infinite extensions of the previous character abc*express ab,abc,abcc,abccc etc.

+ One or infinite extension of the previous character abc+express abc,abcc,abccc etc.

？ Zero or one extension of the previous character abc?express ab,abc

| Either left or right expression abc|def express abc,def

{m} Extend previous character m second ab{2}c express abbc

{m,n} Extend previous character m to n Times (including) n (Times) ab{1,2}express abc,abbc

^ Matches the beginning of a string ^abc express abc And at the beginning of a string

$ Match end of string abc$express abc And at the end of a string


() Group mark, which can only be used internally|Operator (abc)express abc,(abc|def)express abc,def

\d Number, equivalent to[0-9]

Then you need to use PT segmentation, that is | [P|T]

split segmentation method

re.split segmentation is different from general split

re.split(pattern, string[, maxsplit=0, flags=0])

pattern: matching string
String: the string to be segmented
Maxplit: number of separation times. The default value is 0 (i.e. unlimited times)
flags: flag bit, which is used to control the matching method of regular expressions, such as case sensitivity, multi line matching, etc

The general split is

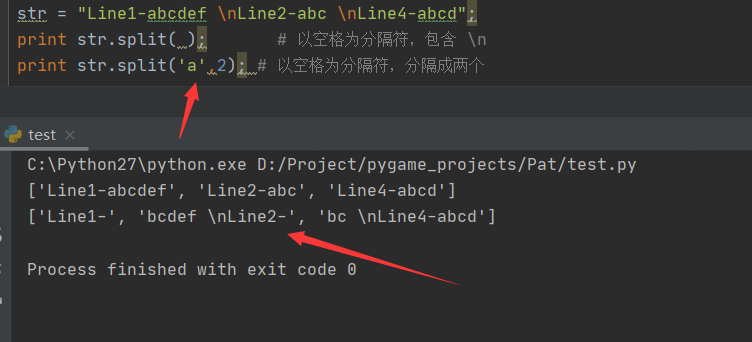
str.split(str="", num=string.count(str))

str = "Line1-abcdef \nLine2-abc \nLine4-abcd"
print str.split( ) # Space delimited, including \n 
print str.split(' ', 1 ) # Separate into two with a space as a separator

• str -- separator, which defaults to all empty characters, including spaces, line breaks (\ n), tabs (\ t), etc.
• num -- number of divisions. The default is - 1, which separates all.

Here, it is divided twice with a as the delimiter

  So the code is:

import re


def check(n):
    s = list()
    for i in range(0, n):
        s.append(input())
    for i in range(0, n):
        if re.match(r'A*PA+TA*', s[i]):
            # Write regular matches based on inference
            a = re.split(r'[P|T]', s[i])
            # adopt split with PT It will be divided into three parts
            # a paragraph b paragraph c paragraph
            if a[2] == a[0] * len(a[1]):
                print('YES')
            else:
                print('NO')
        else:
            print('NO')


if __name__ == '__main__':
    n = int(input())
    check(n)