PAT class a 1119 pre - and post order Traversals
Suppose that all the keys in a binary tree are distinct positive integers. A unique binary tree can be determined by a given pair of postorder and inorder traversal sequences, or preorder and inorder traversal sequences. However, if only the postorder and preorder traversal sequences are given, the corresponding tree may no longer be unique. Now given a pair of postorder and preorder traversal sequences, you are supposed to output the corresponding inorder traversal sequence of the tree. If the tree is not unique, simply output any one of them. Input Specification: Each input file contains one test case. For each case, the first line gives a positive integer N (≤ 30), the total number of nodes in the binary tree. The second line gives the preorder sequence and the third line gives the postorder sequence. All the numbers in a line are separated by a space. Output Specification: For each test case, first printf in a line Yes if the tree is unique, or No if not. Then print in the next line the inorder traversal sequence of the corresponding binary tree. If the solution is not unique, any answer would do. It is guaranteed that at least one solution exists. All the numbers in a line must be separated by exactly one space, and there must be no extra space at the end of the line. Sample Input 1: 7 1 2 3 4 6 7 5 2 6 7 4 5 3 1 No blank lines at the end Sample Output 1: Yes 2 1 6 4 7 3 5 No blank lines at the end Sample Input 2: 4 1 2 3 4 2 4 3 1 No blank lines at the end Sample Output 2: No 2 1 3 4 No blank lines at the end
First order traversal and second order traversal determine the middle order traversal. The constructed binary tree is not necessarily unique. You can see the following links
https://blog.csdn.net/waple_0820/article/details/81837875
The summary assumes that if a parent node has only one child node, there is no way to determine whether the child node is a left node or a right node (because the first order traversal is about the root, and the second order is left and right roots)
For example, the first order is 1 2 3 4, and the second order is 2 4 3 1. The constructed binary tree has the following two cases:
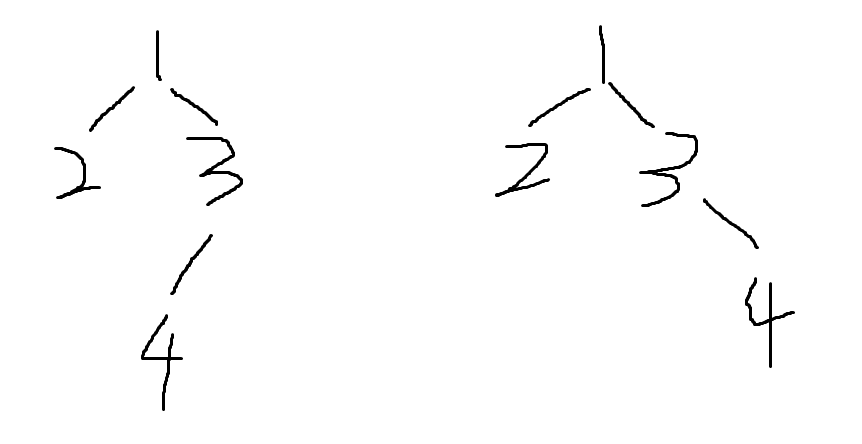
The construction process is as follows: each step needs to distinguish the root node and its left and right subtrees. Use the above example to illustrate:
1. The first number traversed in sequence is the root node 1 of the binary tree
2. Now look for the left and right subtrees of root node 1, that is, find the range of the left and right subtrees in the pre order and post order (the nodes of the left subtree must appear earlier than the nodes of the right subtree. Assuming that the first element to the i-th element in the preamble is the left subtree, then the i + 1 element to the N-1 element is the right subtree; corresponding to the left subtree from the 0-th element to the j-th element in the postsequence, then the j + 1 element to the N-2 element is the right subtree) , in this question, the next element under the root node in the first order is 2, so 2 is the root node of the left subtree. Find the location of 2 in the second order and find that there is no element in front of 2, that is, the root node is 1 and there is only one element in the left subtree (this is because the second order is the left and right roots. If there are other elements in the left subtree except 2, it will certainly appear before 2 in the second order) , the right subtree is 4 3
3. According to the previous step, we determined that 1 is the root node, the left subtree is 2, and the right subtree is 4 3. Therefore, continue to operate the left subtree and the right subtree according to the previous step. The first order of the left subtree is 2, the second order is 2, the first order of the right subtree is 3 4, and the second order is 4 3 (it can be seen here that the root of the right subtree is 3, and there is still a 4. It is impossible to determine whether it is the left node or the right node of 3, so this is a binary tree that cannot be unique.)
The following is an example of the title:
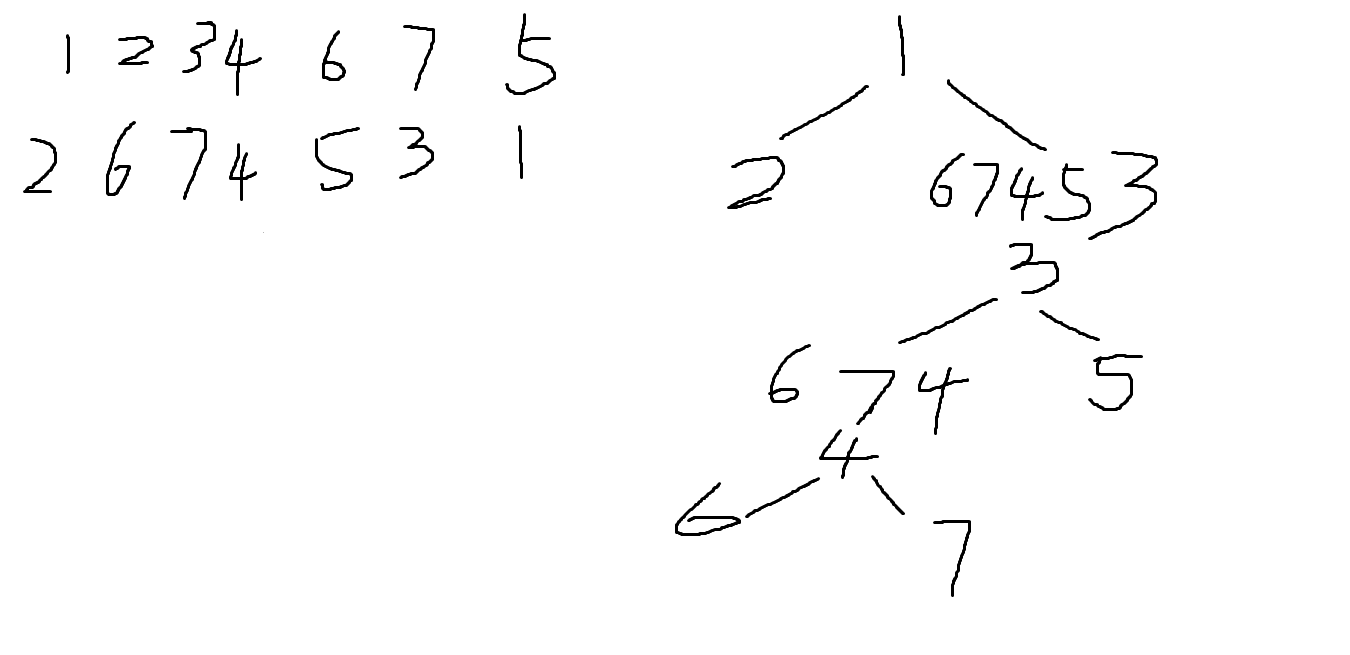
Recursive rules:
*1. The root node is the first element of the current sequence and the last element of the subsequent sequence
2. The next element of the first element in the first sequence is the root node of the left subtree. The range from the corresponding position of the element in the subsequent sequence to the first element in the subsequent sequence is the left subtree node; the range from the next element in the position of the subsequent sequence to the previous element of the end element is the right subtree node.
(1) If the left or right subtree has an even number of nodes, the tree is not unique; otherwise, it is unique
(2) If the start point of the left or right subtree is greater than the end point, it means that there is no left or right subtree in the root node
(3) If the start point of the left or right subtree is equal to the end point, it means that the left or right subtree is a leaf node
**
Here is my code:
#include <iostream>
#include <vector>
using namespace std;
struct node {
int data;
node* lchild;
node* rchild;
}tree[50];
vector<int> pre;
vector<int> post;
int n;
int loc = 0;
node* creat() {
tree[loc].lchild = tree[loc].rchild = nullptr;
return &tree[loc++];
}
bool flag = true;
node* build(int s1, int e1, int s2, int e2) {
if (s1 > e1 || s2 > e2) {
return nullptr;
}
node* root = creat();
root->data = pre[s1];
if (s1== e1) {
return root;
}
else {
int temp = pre[s1 + 1];
int left_root;
for (int i = s2; i <= e2; ++i) {
if (temp == post[i]) {
left_root = i;
break;
}
}
if ((left_root - s2 + 1) % 2 == 0 || (e2 - 1 - left_root) % 2 == 0) {
flag = false;
}
root->lchild = build(s1 + 1, s1 + left_root - s2 + 1, s2, left_root);
root->rchild = build(s1 + left_root - s2 + 2, e1, left_root + 1, e2 - 1);
return root;
}
}
bool out_flag = false;
void inorder(node* root) {
if (root->lchild != nullptr) {
inorder(root->lchild);
}
if (out_flag == false) {
cout << root->data;
out_flag = true;
}
else {
cout << ' ' << root->data;
}
if (root->rchild != nullptr) {
inorder(root->rchild);
}
}
int main() {
cin >> n;
pre.resize(n);
post.resize(n);
for (int i = 0; i < n; ++i) {
cin >> pre[i];
}
for (int i = 0; i < n; ++i) {
cin >> post[i];
}
node* root = build(0, n - 1, 0, n - 1);
if (flag == true) {
cout << "Yes" << endl;
}
else {
cout << "No" << endl;
}
inorder(root);
cout << endl;
return 0;
}
The following code does not need to build a binary tree, but traverses in sequence in the process of traversing pre order and post order:
In fact, this process is the same as the above process of building a binary tree, except that the steps of building a tree are missing. Note that in addition to the operation of adding elements to the array in the middle of recursion in the template of medium order traversal, the elements should also be added to the array when s1 == e1, because the elements are leaf nodes at this time, which need to be added according to the code process
#include <iostream>
#include <vector>
using namespace std;
vector<int> pre;
vector<int> post;
vector<int> in;
int n;
bool unique = true;
void getin(int s1,int e1,int s2,int e2){
if(s1 > e1||s2 > e2){
return;
}
if(s1 == e1){
in.push_back(pre[s1]);
return;
}
int left_root = pre[s1 + 1];
int rootidx;
for(int i = s2;i <= e2;++i){
if(post[i] == pre[s1 + 1]){
rootidx = i;
break;
}
}
if((rootidx - s2 + 1) % 2 == 0||(e2 - rootidx - 1) % 2 == 0){
unique = false;
}
getin(s1 + 1,rootidx - s2 + s1 + 1,s2,rootidx);
in.push_back(pre[s1]);
getin(rootidx - s2 + s1 + 2,e1,rootidx + 1,e2 - 1);
return;
}
int main(){
cin >> n;
pre.resize(n);
post.resize(n);
for(int i = 0;i < n;++i){
cin >> pre[i];
}
for(int i = 0;i < n;++i){
cin >> post[i];
}
getin(0,n - 1,0,n - 1);
if(unique == false){
cout << "No" << endl;
}
else{
cout << "Yes" << endl;
}
for(int i = 0;i < n;++i){
if(i != 0){
cout << ' ';
}
cout << in[i];
}
cout << endl;
return 0;
}
It should also be noted that if the format of the test point is wrong, you can see if there is no line feed at the end of the output, and there is an extra space after the last element of medium order traversal