P3203 [HNOI2010] Missile Flying Sheep

Title Description

See: P3203 [HNOI2010] Missile Flying Sheep

solution

This is a naked question of LCT.

But I don't want to solve this problem with LCT (In fact is not LCT~QAQ)

So we began to divide it up vigorously.

Considering dividing the bouncing device into blocks, we need to know how many times we need to jump in a block and which node to reach after jumping out of this block, so as to ensure that the information of each block will not affect the information of other blocks, and we can use DP in.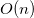The above information is preprocessed in time.

Each time the query jumps to a later block, the answer is counted along the way.

Because of the independence between blocks, direct violent modification of a piece of information that needs to be modified can be done.

Time complexity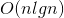

Code

#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+50;
int a[MAXN],color[MAXN],n,Size;
struct fnode{int x,y; } f[MAXN];
inline int read()
{
	int f=1,x=0; char c=getchar();
	while (c<'0'||c>'9') { if (c=='-') f=-1; c=getchar(); }
	while (c>='0'&&c<='9') { x=(x<<3)+(x<<1)+(c^48); c=getchar(); }
	return x*f;
}
void change(int i)                                                          //Find the information of i position
{
	if (i+a[i]<=n)
	{
		if (color[i]==color[i+a[i]]) f[i]=(fnode){f[i+a[i]].x,f[i+a[i]].y+1};
		else f[i]=(fnode){i+a[i],1};
	}
	else f[i]=(fnode){-1,1};
}
int main()
{
	n=read(),Size=trunc(sqrt(n));
	for (int i=1;i<=n;i++) a[i]=read(),color[i]=(i-1)/Size+1;
	for (int i=n;i>=1;i--) change(i);                                       //Preprocessing 
	//for (int i=1;i<=n;i++) cout<<i<<":"<<f[i].x<<" "<<f[i].y<<endl;
	
	int Case=read();
	while (Case--)
	{
		int opt=read(),x=read()+1;                                          //The label starts at 0. 
		if (opt==1)
		{
			int ans=0;
			while (x!=-1) ans+=f[x].y,x=f[x].x;                             //Statistical answers 
			printf("%d\n",ans);
		}
		else
		{
			int y=read(); a[x]=y;
			for (int i=color[x]*Size;i>=(color[x]-1)*Size+1;i--) change(i); //Violent modification in the same way as pre-processing 
			//for (int i=1;i<=n;i++) cout<<i<<":"<<f[i].x<<" "<<f[i].y<<endl;
		}
	}
	return 0;
}