subject

P2057 [showi2007] vote in good faith

analysis

The modeling of network flow is so ingenious.

We regard the agreed opinion as the source point \ (s \), and the disagreed opinion as the sink point \ (t \).

Then we \ (s \) connect to all the people who agree and \ (t \) connect to all the people who disagree. The traffic volume is 1, which indicates the cost of direct conflict with the original scheme. The traffic volume is 1, which indicates the cost of changing the opinion. After the person changes his opinion, he or she will change from agree to disagree with the original scheme A friend with conflicting opinions does not have conflicting opinions with him, so the cost is 1.

We want everyone to agree that there is no difference between the source point and the sink point, that is, there is no connection, so we need to find the minimum cut, according to the minimum cut maximum flow theorem, that is, to find the maximum flow.

That's the way it's done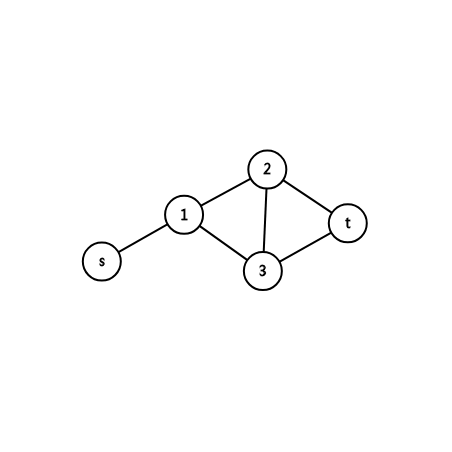

Code

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
const int INF = 0x3f3f3f3f;
int n, m, s, t, num = 1;
int head[N], cur[N], dep[N];
class node {
    public :
        int v, nx, w;
} e[N];

template<class T>inline void read(T &x) {
    x = 0; int f = 0; char ch = getchar();
    while (!isdigit(ch)) f |= (ch == '-'), ch = getchar();
    while (isdigit(ch)) x = x * 10 + ch - '0', ch = getchar();
    x = f ? -x : x;
    return ;
}

inline void add(int u, int v, int w) {
    e[++num].nx = head[u], e[num].v = v, e[num].w = w, head[u] = num;
    e[++num].nx = head[v], e[num].v = u, e[num].w = 0, head[v] = num;
}

queue<int>q;
bool bfs() {
    memset(dep, 0, sizeof dep);
    memcpy(cur, head, sizeof cur);
    dep[s] = 1;
    q.push(s);
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        for (int i = head[u]; ~i; i = e[i].nx) {
            int v = e[i].v;
            if (e[i].w && !dep[v]) dep[v] = dep[u] + 1, q.push(v);
        }
    }
    return dep[t];
}

int dfs(int u, int flow) {
    if (u == t) return flow;
    int use = 0;
    for (int &i = cur[u]; ~i; i = e[i].nx) {
        int v = e[i].v;
        if (e[i].w && dep[v] == dep[u] + 1) {
            int di = dfs(v, min(flow, e[i].w));
            e[i].w -= di, e[i ^ 1].w += di;
            use += di, flow -= di;
            if (flow <= 0) break;
        }
    }
    return use;
}

int dinic() {
    int ans = 0;
    while (bfs()) ans += dfs(s, INF);
    return ans;
}

int main() {
    memset(head, -1, sizeof head);
    read(n), read(m);
    s = n + 1, t = s + 1;
    for (int i = 1, x; i <= n; ++i) {
        read(x);
        if (x) add(s, i, 1);
        else add(i, t, 1);
    }
    for (int i = 1, x, y; i <= m; ++i) {
        read(x), read(y);
        add(x, y, 1);
        add(y, x, 1);
    }
    printf("%d\n", dinic());
}