Title Description:
Problem solving ideas:
According to the meaning of the question, this question is to select several points on a tree to maximize the point weight, in which the selected points meet two conditions:
- If the parent node is selected, the child node cannot be selected
- If a child node is selected, the parent node cannot be selected
Obviously, the top priority of the problem is how to store a tree or a graph in the program. At this time, the popular adjacency matrix has spatial defects, so we need to use the chain forward star.
Chain forward Star:
Chained forward star is a flexible storage structure. We need to use the structure to implement it in the program.
There is a graph. The relationship between points and edges is:
1 3
2 3
6 4
7 4
4 5
3 5
The actual figure above is:
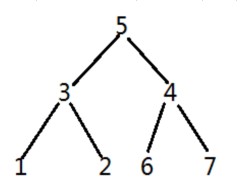
Set structure array
e
e
e represents the relationship between the midpoint and the edge of the point in the diagram, including
h
e
a
d
,
x
,
y
,
n
e
x
t
head,x,y,next
head,x,y,next, then
e
.
x
e.x
e.x represents the starting point,
e
.
y
e.y
e.y represents the target point,
e
.
n
e
x
t
e.next
e.next means and
e
.
x
e.x
e.x is the sequence number of the next side of the same starting point,
e
.
h
e
a
d
e.head
e.head representation
e
.
x
e.x
e. The sequence number of the first side of X.
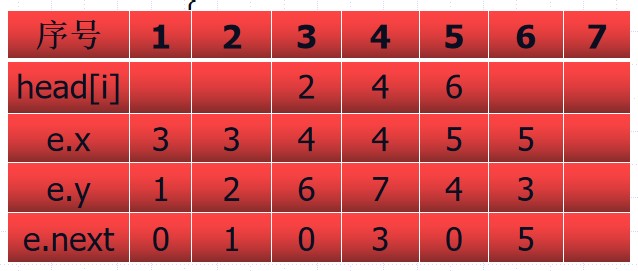
As shown in the figure, it is the state when a linked forward star stores a diagram.
We find the starting point No. 4 according to the header
e
4
.
h
e
a
d
=
4
e_4.head=4
e4. head=4
4
4
The first edge with 4 points as the starting point is numbered
4
4
4, the target point of this edge is
e
4
.
y
=
7
e_4.y=7
e4. y=7, i.e. No
7
7
7 points.
Then observe to
4
4
4 as the next edge of the starting point, the number of the edge is
e
4
.
n
e
x
t
=
3
e_4.next=3
e4. next=3, so the number is
3
3
The side of 3 is
4
4
The second side of 4, the target point is
e
3
.
y
=
6
e_3.y=6
e3.y=6.
If we look at the next side, we find that
e
3
.
n
e
x
t
=
0
e_3.next=0
e3. next=0, that is, there is no next edge, that is, the end pair
4
4
Traversal of 4 points.
Thus, by traversing all the edges of the root node, we can get the child nodes. By repeating this, we can store and traverse a graph.
struct note
{
int x,y,next;
} e[6010];
int head[6010]={0},tot=0; //tot represents the number of edges
void add(int x,int y) //Creates a directed edge between X and Y
{
tot++;
e[tot].x=x;
e[tot].y=y;
e[tot].next=head[x];
head[x]=tot;
}
Tree DP:
After solving the problem of storing graphs, we will consider DP on this tree.
set up
f
i
,
1
/
0
f_{i,1/0}
fi,1/0 , indicates when considering the second
i
i
When i points are selected
/
/
/When not selected, the
i
i
i is the maximum point weight sum of the subtree of the root.
When the parent node is selected, its child nodes cannot be selected; When the parent node is not selected, its child nodes can also be selected or not selected.
The state transition equation is not difficult to give:
f
i
=
{
∑
j
f
j
,
0
choose
The first
i
individual
spot
,
j
by
i
of
son
son
∑
j
m
a
x
(
f
j
,
0
,
f
j
,
1
)
no
choose
The first
i
individual
spot
,
j
by
i
of
son
son
f_ i=\begin{cases} \sum_ {j}f_ {J, 0} & select the ith point, where j is the son of I \ \ \ \ sum_ {j} Max (f {J, 0}, f {J, 1}) & do not select the ith point, j is the son of I \ end{cases}
fi = {∑ J} fj,0 ∑ J} max(fj,0, fj,1) select the ith point, j is the son of i, not the ith point, j is the son of i
Because the tree itself has the nature of recursion, we find a root node, start from the root node, traverse its subtree through the chain forward star, and perform DP recursively.
CODE:
#include <iostream>
#include <cstring>
using namespace std;
struct note
{
int x,y,next;
} e[6010];
int head[6010]={0},tot=0;
void add(int x,int y) //Chain forward star
{
tot++;
e[tot].x=x;
e[tot].y=y;
e[tot].next=head[x];
head[x]=tot;
}
int n,ri[6010]={0},f[6010][2]={0};
bool vis[6010]={false};
void dp(int s) //s is the root node of the current tree
{
f[s][1]=ri[s];
int i=head[s]; //i is the number of the first side of s
while(i)
{
dp(e[i].y); //Handle the target point of this edge and recurse the subtree
f[s][1]=f[e[i].y][0]+f[s][1];
f[s][0]=max(f[e[i].y][1],f[e[i].y][0])+f[s][0];
i=e[i].next; //Next edge
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>ri[i];
int a,b;
for(int i=1;i<n;i++)
{
cin>>a>>b;
add(b,a);
vis[a]=true;
}
for(int i=1;i<=n;i++)
{
if(vis[i]) continue; //Find the root node, that is, the point with penetration of 0
dp(i);
cout<<max(f[i][1],f[i][0]);
break;
}
return 0;
}