Title Description

Xiao T, a quality supervisor, recently checked the quality of a batch of minerals.There are n minerals in this batch, numbered one by one from 1 to n, each of which has its own weight wi and value vi.The process for inspecting minerals is:

1. Given m intervals [Li,Ri];

2. Select a parameter W;

3. For an interval [Li,Ri], the test value Yi of the ore in this interval is calculated:

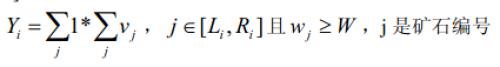
The result Y of this batch of minerals is the sum of the test values for each interval.That is: Y1+Y2...+Ym

If the results of this batch of minerals differ too much from the standard value S given, another batch of minerals needs to be examined.Small T

He didn't want to spend time examining another batch of minerals, so he wanted to keep the results as close as possible by adjusting the value of parameter W.

Standard value S, even if the absolute value of S-Y is the smallest.Please help find this minimum.

Input and Output Formats

Input format:

Enter the file qc.in.

The first row contains three integers, n, m, S, representing the number of ore, the number of intervals, and the standard value.

The next n rows, two integers i n each row, are separated by spaces, and row i+1 represents the weight wi and value vi of the ore No. I.

The next m rows represent intervals, two integers per row separated by a space, and the first i+n+1 row represents the two endpoints Li and Ri of the interval [Li,Ri].Note: Different intervals may overlap or overlap each other.

Output format:

The output file name is qc.out.

The output has only one line and contains an integer representing the minimum value requested.

Input and Output Samples

5 3 15 
1 5 
2 5 
3 5 
4 5 
5 5 
1 5 
2 4 
3 3 

10

Explain

[Sample description of input and output]

When W is selected 4, the test values in the three intervals are 20, 5 and 0, respectively. The test results for this batch of minerals are 25.

The minimum difference between time and standard value S is 10.

[Data Range]

For 10% of the data, 1 < n, m < 10;

For 30% of the data, 1 < n, m < 500;

For 50% of the data, 1 < n, m < 5,000;

For 70% of the data, 1 < n, m < 10,000;

For 100% of the data, 1 < n, m < 200,000, 0 < wi, VI < 10^6, 0 < S < 10^12, 1 < Li < Ri < n.

Write a Moose team at the beginning.We found that Moquoi can only pass the example.

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<cmath>
 5 #include<queue>
 6 #include<algorithm>
 7 #define lli long long int 
 8 using namespace std;
 9 const lli MAXN=200001;
10 void read(lli &n)
11 {
12     char c='+';lli x=0;bool flag=0;
13     while(c<'0'||c>'9')
14     {c=getchar();if(c=='-')flag=1;}
15     while(c>='0'&&c<='9')
16     {x=x*10+(c-48);c=getchar();}
17     flag==1?n=-x:n=x;
18 }
19 struct node
20 {
21     lli w,v;
22 }kuang[MAXN];
23 struct xw
24 {
25     lli l,r,id;
26 }q[MAXN];
27 lli n,m,s;
28 lli ans=0x7ffffff;
29 lli pos[MAXN];
30 lli base;
31 lli num,va;
32 lli comp(const xw &a,const xw &b)
33 {
34     if(pos[a.l]==pos[b.l])
35     return a.r<b.r;
36     else 
37     return pos[a.l]<pos[b.l];
38 }
39 void add(lli p,lli need)
40 {
41     if(kuang[p].w>=need)
42     {
43         num++;
44         va+=kuang[p].v;
45     }
46 }
47 void dele(lli p,lli need)
48 {
49     if(kuang[p].w>=need)
50     {
51         num--;
52         va-=kuang[p].v;
53     }
54 }
55 lli pd(lli need)
56 {
57     lli ll=1,rr=0;
58     lli now=0;
59     num=0;va=0;
60     for(lli i=1;i<=m;i++)
61     {
62         for(;ll<q[i].l;ll++)
63             add(ll-1,need);
64         for(;ll>q[i].l;ll--)
65             dele(ll,need);
66         for(;rr>q[i].r;rr--)
67             dele(rr,need);
68         for(;rr<q[i].r;rr++)
69             add(rr+1,need);    
70         now+=num*va;
71     }
72     if(now-s<ans&&now-s>0)
73     {
74         ans=now-s;
75         return 1;
76     }
77     else return 0;
78 }
79 int main()
80 {
81     read(n);read(m);read(s);
82     base=sqrt(n);
83     for(lli i=1;i<=n;i++)
84         pos[i]=(i-1)/base+1;
85     for(lli i=1;i<=n;i++)
86     {read(kuang[i].w);read(kuang[i].v);}
87     for(lli i=1;i<=m;i++)
88     {
89     read(q[i].l);read(q[i].r);
90     }
91     sort(q+1,q+m+1,comp);
92     
93     lli ll=0,rr=5;
94     for(lli i=-500;i<=500;i++)
95         pd(i);
96     printf("%lld",ans);
97     return 0;
98 }