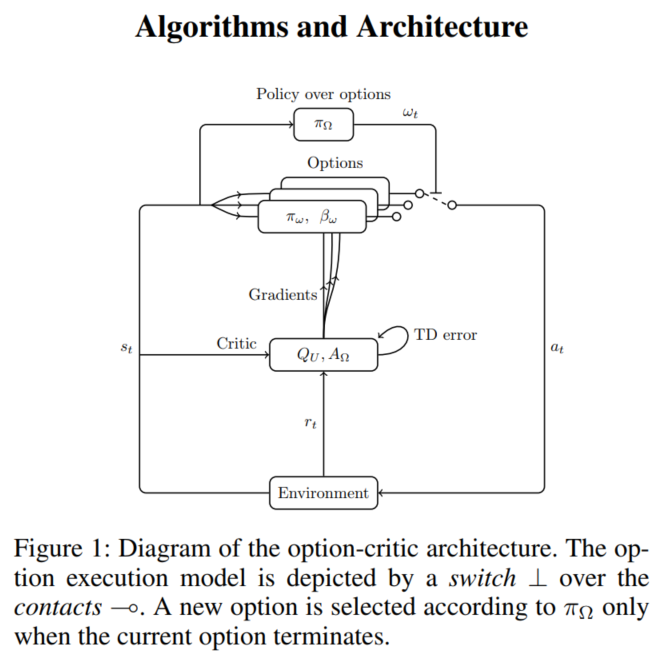
Option critical code analysis

1.option-critic_network.py analysis

a. State Network

• state_ The model performs three-layer convolution on the input, compresses it into a one-dimensional vector, and inputs it to the full connection layer to obtain flatted * weights4 + bias1.
• My understanding: this process is to extract the features in the image and take them as observable state quantities for further processing.
• q_model calculates matmul(input, q_weights1) + q_bias. q_ The input of model is state_ Output of model.
• In this process, the variable network_params includes parameters of three filter s, weights4 and bias1; Q_params includes q_weights1，q_bias1.
  Why do we convolute the image?

Through the mathematical operation of the original image and convolution kernel, some specified features of the image can be extracted.

What is two-dimensional convolution?

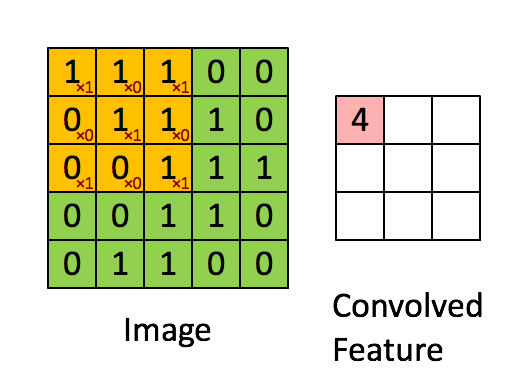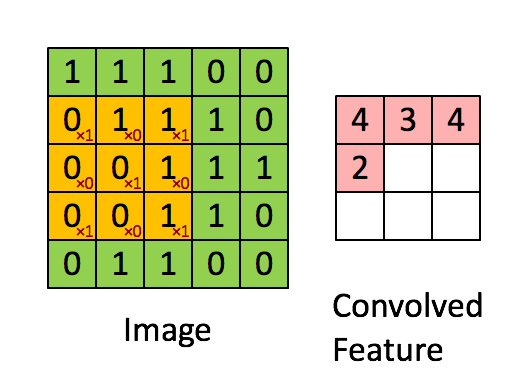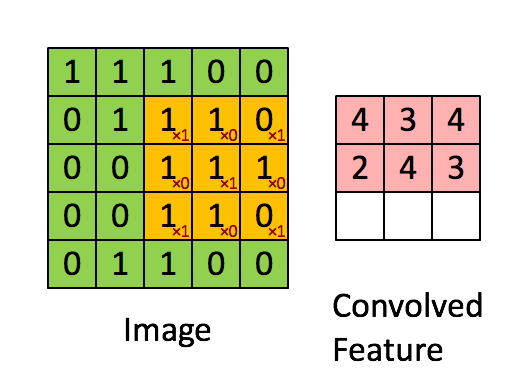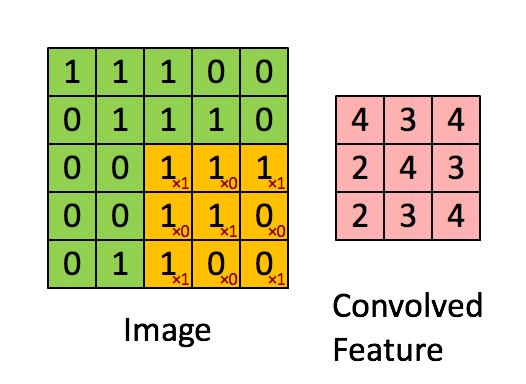
In the picture, the green 5x5 box can be regarded as the local pixel matrix of a gray image, the moving yellow 3x3 box is called the kernel, and the pink box is the result of convolution processing.

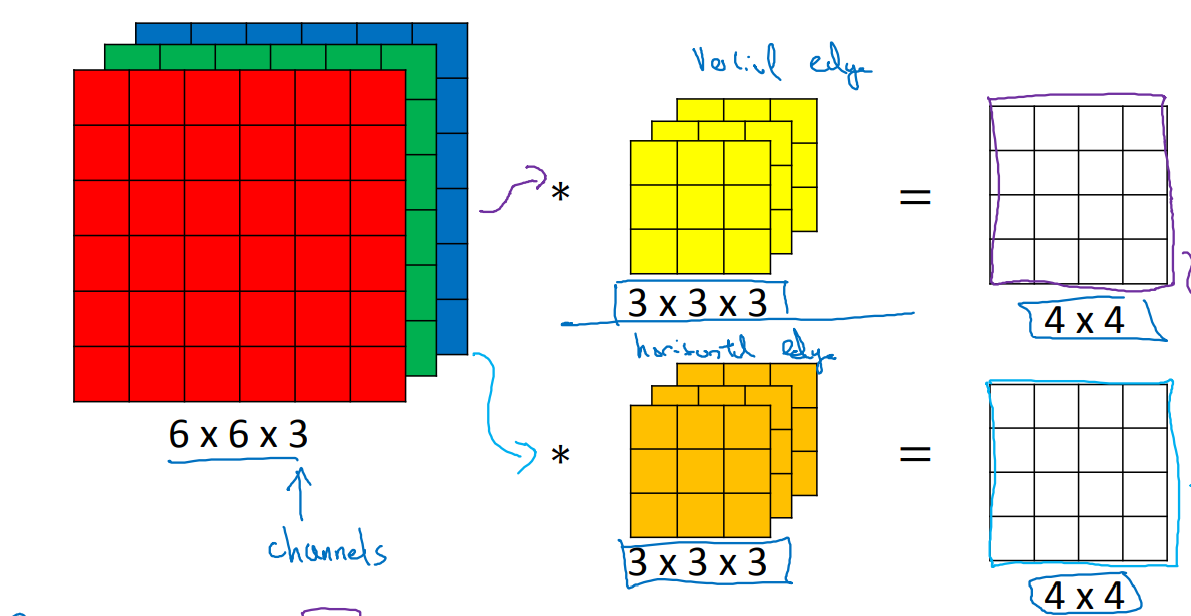
The concepts of filter and kernel in neural networks
Kernel: the kernel is a two-dimensional matrix, long × Wide;
Filter: the filter is a three-dimensional cube, long × Wide × Depth, where depth is the number of cores; it can be said that the kernel is the basic element of the filter, and multiple cores form a filter.
The concept of channels in neural networks
During CNN processing, there are input channels and output channels; where, the number of input channels = the depth of input data; the number of output channels = the depth of output data.

Recommend Li Hongyi's convolution neural network course: https://www.bilibili.com/video/BV1F4411y7o7?p=7&spm_id_from=pageDriver

Convolution processing function in tensorflow

tf.nn.conv2d
conv2d(
    input,
    filter,
    strides,
    padding,
    use_cudnn_on_gpu=True,
    data_format='NHWC',
    name=None)
Args:
	• input: Entered tensor，The convoluted image, conv2d requirement input It must be four-dimensional. The four dimensions are[batch, in_height, in_width, in_channels]，
    Namely batch size，Enter the height and width of the image and the number of channels for a single image.
	• filter: Convolution kernel is also required to be four-dimensional,[filter_height, filter_width, in_channels, out_channels]The four dimensions represent the height and width of the convolution kernel, the number of channels of the input image and the number of convolution output channels respectively.
	• strides: Step size, that is, the distance that the convolution kernel moves each time in the process of convolution with the image, is generally defined as[1，stride_h,stride_w,1]，stride_h And stride_w Represents the moving step in the high direction and the wide direction respectively, and the first 1 represents the moving step in the batch The last 1 represents the step moved in the channel dimension, while the current tensorflow regulations: strides[0] = strides[3] = 1，That is, skipping is not allowed bacth And channels, in the previous dynamic diagram stride_h And stride_w All 1
	• padding: Edge processing method, value is“ SAME" And“ VALID".
    Because the convolution kernel has size, when the convolution kernel moves to the edge, some elements in the convolution kernel do not have corresponding pixel values to match it.
    Select at this time“ SAME"Mode, fill zero at the corresponding position and continue to complete the convolution operation strides by[1,1,1,1]If the image size remains unchanged before and after convolution, it is“ SAME". 
    If selected“ VALID"Mode, no convolution operation is performed at the edge, and the size of the image will become smaller after operation. 
Returns:
A Tensor. 4 Dimensional tensor

        self.inputs = tf.p0laceholder(
            shape=[None, 84, 84, 4], dtype=tf.uint8, name="inputs")
        scaled_image = tf.to_float(self.inputs) / 255.0

create_state_network

def state_model(self, input, kernel_shapes, weight_shapes):
        # kernel_shapes=[[8, 8, 4, 32], [4, 4, 32, 64], [3, 3, 64, 64]]
        # [filter_height, filter_width, in_channels, out_channels]
        #  weight_shapes=[[3136, 512]]
        
        weights1 = tf.get_variable(
            "weights1", kernel_shapes[0],
            initializer=tf.contrib.layers.xavier_initializer())
        weights2 = tf.get_variable(
            "weights2", kernel_shapes[1],
            initializer=tf.contrib.layers.xavier_initializer())
        weights3 = tf.get_variable(
            "weights3", kernel_shapes[2],
            initializer=tf.contrib.layers.xavier_initializer())
        weights4 = tf.get_variable(
            "weights5", weight_shapes[0],
            initializer=tf.contrib.layers.xavier_initializer())
        bias1 = tf.get_variable(
            "q_bias1", weight_shapes[0][1],
            initializer=tf.constant_initializer())
        # Convolve
        conv1 = tf.nn.relu(tf.nn.conv2d(
            input, weights1, strides=[1, 4, 4, 1], padding='VALID'))
        conv2 = tf.nn.relu(tf.nn.conv2d(
            conv1, weights2, strides=[1, 2, 2, 1], padding='VALID'))
        conv3 = tf.nn.relu(tf.nn.conv2d(
            conv2, weights3, strides=[1, 1, 1, 1], padding='VALID'))
        # Flatten and Feedforward
        flattened = tf.contrib.layers.flatten(conv3)
        net = tf.nn.relu(tf.nn.xw_plus_b(flattened, weights4, bias1))

        return net

q_model

    def q_model(self, input, weight_shape):
        weights1 = tf.get_variable(
            "q_weights1", weight_shape,
            initializer=tf.contrib.layers.xavier_initializer())
        # This initializer is used to make the variance of the output of each layer as equal as possible.

        bias1 = tf.get_variable(
            "q_bias1", weight_shape[1],
            initializer=tf.constant_initializer())
        # Initializes a variable to a given constant and initializes all provided values.
        return tf.nn.xw_plus_b(input, weights1, bias1)
    # Calculate matmul(input, q_weights1) + q_bias.

b. Prime Network

• Prime Network is the main network that needs to be updated at any time. It is mainly composed of create_state_network and target_q_model.
• The process of create_state_network is similar to the state_network above. The image is convoluted in three layers, and then the observed state value is obtained through a full connection layer. Among them, the shape of filtersinput is the same for both networks. That is, the parameters of the two networks are the same and corresponding. In other words, create_state_network copies the state_network.
• target_q_model implements target_Q_out = input * weights1 + bias1, and obtains the action value function Q π ( s , a ) Q_\pi(s,a) Qπ​(s,a).
• target_network_params includes the parameters in create_state_network. target_Q_params includes weights1 and bias1.
• Update the parameters in the target network (Prime_Network) with the current network (State_Network). tau=0.001.

        self.update_target_network_params = \
            [self.target_network_params[i].assign(
                tf.multiply(self.network_params[i], self.tau) +
                tf.multiply(self.target_network_params[i], 1. - self.tau))
             for i in range(len(self.target_network_params))]

create_state_network

    def create_state_network(self, scaledImage):
        # Convolve
        # kernel_size refers to the size of convolution kernel; stripe step size; padding edge processing method: 'VALID' convolution calculation is not performed at the edge
        # Out_height = round ((in_height - floor (filter_height / 2) * 2) / strips_height) floor means rounding down, and round means rounding
        # num_outputs is the number of output channels, equal to the number of filters
        # filters:Integer, the dimensionality of the output space (i.e. the number of filters in the convolution).
        conv1 = slim.conv2d(
            inputs=scaledImage, num_outputs=32, kernel_size=[8, 8], stride=[4, 4],
            padding='VALID', biases_initializer=None)
        conv2 = slim.conv2d(
            inputs=conv1, num_outputs=64, kernel_size=[4, 4], stride=[2, 2],
            padding='VALID', biases_initializer=None)
        conv3 = slim.conv2d(
            inputs=conv2, num_outputs=64, kernel_size=[3, 3], stride=[1, 1],
            padding='VALID', biases_initializer=None)
        # Flatten and Feedforward
        flattened = tf.contrib.layers.flatten(conv3)
        net = tf.contrib.layers.fully_connected(
            inputs=flattened,
            num_outputs=self.h_size,
            activation_fn=tf.nn.relu)

        return net

target_q_model

    def target_q_model(self, input, weight_shape):
        weights1 = tf.get_variable(
            "target_q_weights1", weight_shape,
            initializer=tf.contrib.layers.xavier_initializer())
        bias1 = tf.get_variable(
            "target_q_bias1", weight_shape[1],
            initializer=tf.constant_initializer())
        return tf.nn.xw_plus_b(input, weights1, bias1)

c. Action Network

• Get the policy value function action_probs: π ω , θ ( a ∣ s ) \pi_{\omega,\theta}{(a|s)} πω,θ​(a∣s)

• After state_model three-layer convolution and one full connection layer, the image outputs 4x4x64 neurons to represent the observable state quantity of the image.

• With a full connection layer π ω , θ ( a ∣ s ) \pi_{\omega,\theta}{(a|s)} π ω,θ (a ∣ s) function approval. action_params includes the parameters of the full connection layer.

• state_out is the output of state_mode, shape=[4,4,64]; action_dim=6; option_dim=8; h_size=512

tensor operation

Arithmetic operation	describe
tf.add(x,y)	Add x and y element by element
tf.subtract(x,y)	Subtract x and y element by element
tf.multiply(x,y)	Multiply x and y element by element
f.divide(x,y)	Divide x and y element by element
tf.math.mod(x,y)	Remainder x element by element

        self.action_input = tf.concat(
            [self.state_out, self.state_out, self.state_out, self.state_out,
             self.state_out, self.state_out, self.state_out, self.state_out], 1)
        self.action_input = tf.reshape(
            self.action_input, shape=[-1, self.o_dim, 1, self.h_size])
        oh = tf.reshape(self.options_onehot, shape=[-1, self.o_dim, 1])
        self.action_input = tf.reshape(
            tf.reduce_sum(
                tf.squeeze(
                    self.action_input, [2]) * oh, [1]),#Line summation
            shape=[-1, 1, self.h_size])
        # tf.reduce_sum this function calculates the sum of elements in each dimension of a tensor

        self.action_probs = tf.contrib.layers.fully_connected(
            inputs=self.action_input,
            num_outputs=self.a_dim,
            activation_fn=tf.nn.softmax)
        self.action_probs = tf.squeeze(self.action_probs, [1])
        self.action_params = tf.trainable_variables()[
            len(self.network_params) + len(self.target_network_params) +
            len(self.Q_params) + len(self.target_Q_params):]

d. Termination Network

• termination_model uses the full connection layer tf.nn.sigmoid(tf.nn.xw_plus_b(input, weights1, bias1)) to terminate the function option_term_prob β ω , ϑ ( s ) \beta_{\omega,\vartheta}(s) βω,ϑ (s) function approval.
• The parameters of the neural network are included in the termination_params. Note that both termination_params and action_params belong to the parameters of the option policy.
• next_option_term_prob indicates β ω , ϑ ( s ′ ) \beta_{\omega,\vartheta}(s^{'}) βω,ϑ​(s′)

        with tf.variable_scope("termination_probs") as term_scope:
            self.termination_probs = self.apply_termination_model(
                tf.stop_gradient(self.state_out))# Truncate the gradient of the transfer.
            term_scope.reuse_variables()
            self.next_termination_probs = self.apply_termination_model(
                tf.stop_gradient(self.next_state_out))

        self.termination_params = tf.trainable_variables()[-2:]

        self.option_term_prob = tf.reduce_sum(
            self.termination_probs * self.options_onehot, [1])
        self.next_option_term_prob = tf.reduce_sum(
            self.next_termination_probs * self.options_onehot, [1])

        self.reward = tf.placeholder(tf.float32, [None, 1], name="reward")
        self.done = tf.placeholder(tf.float32, [None, 1], name="done")
        # self.disc_option_term_prob = tf.placeholder(tf.float32, [None, 1])

        disc_option_term_prob = tf.stop_gradient(self.next_option_term_prob)

termination_model

    def termination_model(self, input, weight_shape):
        weights1 = tf.get_variable(
            "term_weights1", weight_shape,
            initializer=tf.contrib.layers.xavier_initializer())
        bias1 = tf.get_variable(
            "term_bias1", weight_shape[1],
            initializer=tf.constant_initializer())
        return tf.nn.sigmoid(tf.nn.xw_plus_b(input, weights1, bias1))

e. Update of actor and critical networks

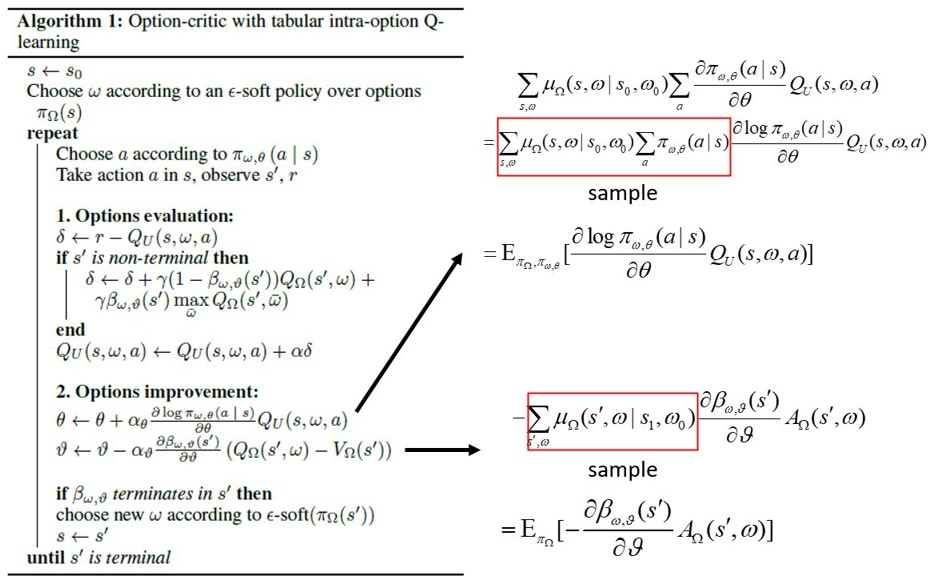
• The update of Actor network is divided into two parts: term_gradient represents the optimization target expectation involving termination function, and policy_gradient represents the optimization target expectation involving policy function. For details, please refer to the figure below.
  

• However, the optimization objective function of the option policy function is not completely consistent with that in the algorithm. The entropy of action_probs is added to the optimization function in the code, and the exploration rate of entropy is set to 0.01.

 # actor updates
        self.value = tf.stop_gradient(
            tf.reduce_max(self.Q_out, reduction_indices=[1]))

        self.disc_q = tf.stop_gradient(tf.reduce_sum(
            self.Q_out * self.options_onehot, [1]))
        self.picked_action_prob = tf.reduce_sum(
            self.action_probs * self.actions_onehot, [1])
        actor_params = self.termination_params + self.action_params
        # entropy is used. Is SAC algorithm referenced?
        entropy = - tf.reduce_sum(self.action_probs *
                                  tf.log(self.action_probs))
        # picked_action_prob is the option policy function
        policy_gradient = - tf.reduce_sum(tf.log(self.picked_action_prob) * y) - \
            entropy_reg * entropy
        # option_term_prob is the termination function
        self.term_gradient = tf.reduce_sum(
            self.option_term_prob * (self.disc_q - self.value))
        self.loss = self.term_gradient + policy_gradient
        grads = tf.gradients(self.loss, actor_params)
        self.actor_updates = tf.train.AdamOptimizer().apply_gradients(zip(grads, actor_params))

• Critic al network update part: use the time difference algorithm to evaluate the option action value of the current network Q U ( s , ω ) Q_{U}(s,\omega) QU​(s, ω) [when an option is selected in a certain state, the total revenue generated after taking an action option_Q_out] is updated.
• Target network option state value target_Q_out represents the total revenue generated after selecting an option in a certain state Q Ω ( s , ω ) Q_{\Omega}(s,\omega) QΩ​(s,ω)

        '''Time difference algorithm:
        disc_option_term_prob:Termination function beta
        tf.reduce_sum(self.target_Q_out * self.options_onehot, [1]): option Value function
        tf.reduce_max(self.target_Q_out, reduction_indices=[1]):calculation option Optimal value
        self.done:judge s'Whether to terminate, the termination is 1.
        '''
        y = tf.squeeze(self.reward, [1]) + \
            tf.squeeze((1 - self.done), [1]) * \
            gamma * (
                (1 - disc_option_term_prob) *
                tf.reduce_sum(self.target_Q_out * self.options_onehot, [1]) +
                disc_option_term_prob *
                tf.reduce_max(self.target_Q_out, reduction_indices=[1]))# Calculate the maximum value of elements in each dimension of a tensor

        y = tf.stop_gradient(y)

        option_Q_out = tf.reduce_sum(self.Q_out * self.options_onehot, [1])# target_Q_out indicates the state of s'
        td_errors = y - option_Q_out
        # self.td_errors = tf.squared_difference(self.y, self.option_Q_out)
        '''take td_cost It is divided into quadratic part and linear part, but in the code clip_delta=0，The linear part is ignored'''
        if clip_delta > 0:
            quadratic_part = tf.minimum(abs(td_errors), clip_delta)
            linear_part = abs(td_errors) - quadratic_part
            td_cost = 0.5 * quadratic_part ** 2 + clip_delta * linear_part
        else:
            td_cost = 0.5 * td_errors ** 2

        # critic updates
        '''critic_cost->td_cost-> td_errors->Q_out-> network_params+Q_params
        self.network_params = tf.trainable_variables()[:-2]
        #  Three layer convolution and full connection layer processing, a total of 3 convolution kernel parameters + full connection 1 weight + full connection 1 deviation
        self.Q_params = tf.trainable_variables()[-2:]
        # q_weights1 ,q_bias. '''
        self.critic_cost = tf.reduce_sum(td_cost)
        critic_params = self.network_params + self.Q_params
        grads = tf.gradients(self.critic_cost, critic_params)
        self.critic_updates = tf.train.AdamOptimizer().apply_gradients(zip(grads, critic_params))
        # apply_gradients uses the calculated gradient to update the corresponding variable
        # self.critic_updates = tf.train.RMSPropOptimizer(
        #     self.learning_rate, decay=0.95, epsilon=0.01).apply_gradients(zip(grads, critic_params))