Operating system experiment - disk scheduling algorithm (FIFS SSTF SCAN)

1, Purpose of the experiment

1. Understand the strategy and principle of disk scheduling;
2. Understand and master the disk scheduling algorithms: FCFS, SSTF and SCAN.

2, Experiment content

1. First come, first served (FCFS), Shortest Seek Time First (SSTF) and SCAN are simulated;
2. The three algorithms are compared and analyzed.
3. The input is a set of request access track sequence, and the output is the track of head movement and the total track number of each scheduling algorithm.

3, Experimental principle

1. First come first served algorithm (FCFS):

Service in first come, last come order, not optimized. The simplest scheduling algorithm is the "first come first serve" scheduling algorithm. In fact, this algorithm does not consider the physical location of visitors' requests, but only considers the order of visitors' requests. When the first come first serve algorithm is used to decide the order of waiting for visitors to perform input and output operations, the mobile arm moves back and forth. The first come first serve algorithm takes a long time to find, so the total time to perform input and output operations is also long.

2. Shortest seek time first algorithm (SSTF):

The shortest search time first scheduling algorithm always selects the shortest seeking time request from the waiting visitors to execute first, regardless of the order of visitors' arrival. Compared with the first come first serve and algorithm, it greatly reduces the search time, thus shortens the average time of requesting services for each visitor, and improves the system efficiency. But the shortest search time first (SSTF) scheduling, FCFS will cause the read-write head to move in a large range on the disk, SSTF find the request with the shortest distance from the head (that is, the shortest search time) as the next service object. The SSTF lookup pattern tends to be highly localized, delaying some requested services and even causing infinite delay (also known as starvation).

3. SCAN algorithm:

SCAN algorithm is also called elevator scheduling algorithm. SCAN algorithm is the shortest search time priority algorithm in the forward direction of the head. It eliminates the back and forth movement of the head in the local position of the disk. SCAN algorithm to a large extent eliminates the unfairness of SSTF algorithm, but it is still conducive to the request of the intermediate track. The "elevator scheduling" algorithm is to select the column visitor closest to the current mobile arm from the current position of the mobile arm along the moving direction of the arm. If there is no request for access along the moving direction of the arm, change the moving direction of the arm and select again. However, when the "elevator scheduling" algorithm is implemented, it must not only remember the current position of the read-write head, but also remember the current direction of the mobile arm.

4, The system call function used in the experiment

  The experiment only simulates the implementation of disk scheduling function, and does not need system call function.

5, Experimental requirements

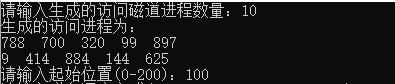
1, The input is a set of request access track sequence, which is randomly generated with the selected track number, and the output is the track of each scheduling algorithm and the total track number;

srand((int)time(NULL));
	cout << "Please enter the number of access track processes generated:";
	int n, m, p=0;
	int flag ;
	string direction;
	cin >> n;
	int a[100];
	for (int i = 0; i < n; i++)
	{
		a[i] = rand() % 1000;
	}cout << "The generated access process is:";
	for (int i = 0; i < n; i++)
	{
		if (i % 5 == 0)
		{
			cout << endl;
		}
		cout << a[i] << "  ";

	}

2. Input the track range 0-1000, input the number of selected tracks 0-1000;

3. Draw the main program flow chart;

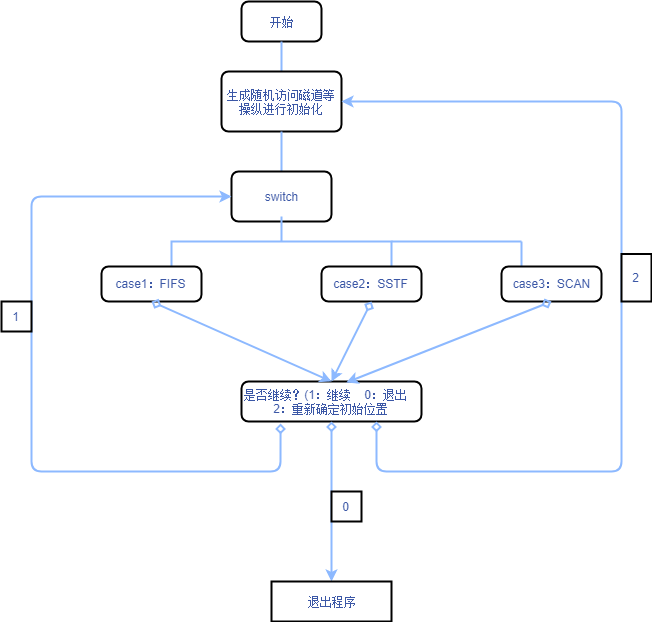
Source code:

include <iostream>
#include<cstdlib>
#include <time.h>

using namespace std;
class DISK
{
private:
	int Movedistance;//Moving distance	
	int Lable[100];//Label pointer
	string Movedirection;//Direction of movement
public:
	int  Calculate_Diference(int a, int b)//Calculate travel distance (absolute value of difference)
	{
		return (a - b > 0 ? a - b : b - a);
	}
	void ShowPath(int a[], int x, int len)//Scheduling process time complexity O(n)
	{
		cout << "from" << x << "Track number one" << endl;
		for (int i = 1; i < len + 1; i++)
		{
			cout << "Track number for next access:" << a[i] << "\t Distance to move:" << Calculate_Diference(a[i], a[i - 1]) << endl;
		}
	}
	void CalculateMoveDistance(int a[], int x, int len)//Time complexity of calculating average seek length O(n)
	{
		double count = 0;;
		double average = 0;
		for (int i = 1; i < len + 1; i++)
		{
			count += Calculate_Diference(a[i], a[i - 1]);
		}
		average = count / len;
		cout << "The average seek length is:" << average << endl;
	}
	void FIFS(int a[], int x, int len)//First come first serve algorithm  
	{
		Lable[0] = x;//The first number in the array is the current track position
		for (int i = 0; i < len; i++)
		{
			Lable[i + 1] = a[i];
		}
		ShowPath(Lable, x, len);
		CalculateMoveDistance(Lable, x, len);
	}
	void SSTF(int a[], int x, int len)//Shortest seek time first
	{
		Lable[0] = x;//The first number in the array is the current track position
		int m = 0;
		int temp = 0;
		for (int i = 0; i < len; i++)//In order to find out the access order, Lalbe [];
		{
			m = i;
			for (int j = i; j < len; j++)//Traverse array a [] to find the track closest to the current head.
			{
				if (Calculate_Diference(a[j + 1], Lable[i]) < Calculate_Diference(a[m], Lable[i]))
				{
					m = j + 1;
					temp = a[j + 1];
				}
				else temp = a[m];
			}
			Lable[i + 1] = temp;
			int temp2 = a[m];//After the track is found, the data found will be replaced to the front of the array, so as to skip the next traverse;
			a[m] = a[i];
			a[i] = temp2;
		}
		ShowPath(Lable, x, len);
		CalculateMoveDistance(Lable, x, len);
	}

	void insertsort(int a[], int len)//Insert sort
	{
		int temp;
		for (int i = 1; i < len; i++)
		{
			temp = a[i];
			int j = i - 1;
			while (j >= 0 && a[j] > temp)
			{
				a[j + 1] = a[j];
				j--;
			}
			a[j + 1] = temp;
		}
	}

	void SCAN(int a[], int x, int len,string  Movedirection)//Scanning algorithm
	{
		Lable[0] = x;//The first number in the array is the current track position
		int m = 0, r = 0, l = 0, r2 = 0, l2 = 0;
		int temp = 0;
		int right[100];
		int rightelse[100];
		int left[100];
		int leftelse[100];
		for (int i = 0; i < len; i++)//When the head moves to the increasing direction of the track, the large tracks are made up of an array, and the other tracks are made up of an array
		{
			if (Lable[0] < a[i])
			{
				right[r] = a[i];
				r++;
			}
			else rightelse[r2] = a[i], r2++;
		}
		for (int i = 0; i < len; i++)//When the head moves in the direction of track reduction, the small tracks are grouped into an array, and the other tracks are grouped into an array
		{
			if (Lable[0] > a[i])
			{
				left[l] = a[i];
				l++;
			}
			else leftelse[l2] = a[i], l2++;
		}
		if (Movedirection == "right")
		{
			insertsort(right, r);//Sort the big ones
			for (int j = 0; j < r; j++)
			{
				Lable[j + 1] = right[j];
			}
			for (int i = 0; i < r2; i++)//Find the rest
			{
				m = i;
				for (int j = i; j < r2; j++)//Traverse array a [] to find the track closest to the current head.
				{
					if (Calculate_Diference(rightelse[j + 1], Lable[i]) < Calculate_Diference(rightelse[m], Lable[i]))
					{
						m = j + 1;
						temp = rightelse[j + 1];
					}
					else temp = rightelse[m];
				}
				Lable[i +r+ 1] = temp;
				int temp2 = rightelse[m];//After the track is found, the data found will be replaced to the front of the array, so as to skip the next traverse;
				rightelse[m] = rightelse[i];
				rightelse[i] = temp2;
			}
			
		}
		if (Movedirection == "left")
		{
			int c = 1;
			insertsort(left, l);//Sort the small ones
			for (int j = l - 1; j >= 0; j--)
			{
				Lable[c] = left[j];
				c++;
			}
			for (int i = 0; i < l2; i++)//Find the rest
			{
				m = i;
				for (int j = i; j < l2; j++)//Traverse array a [] to find the track closest to the current head.
				{
					if (Calculate_Diference(leftelse[j + 1], Lable[i]) < Calculate_Diference(leftelse[m], Lable[i]))
					{
						m = j + 1;
						temp = leftelse[j + 1];
					}
					else temp = leftelse[m];
				}
				Lable[i + l + 1] = temp;
				int temp2 = leftelse[m];//After the track is found, the data found will be replaced to the front of the array, so as to skip the next traverse;
				leftelse[m] = leftelse[i];
				leftelse[i] = temp2;
			}
		}
		ShowPath(Lable, x, len);
		CalculateMoveDistance(Lable, x, len);
	}
};
int main()
{
	DISK disk;
	srand((int)time(NULL));
	cout << "Please enter the number of access track processes generated:";
	int n, m, p=0;
	int flag ;
	string direction;
	cin >> n;
	int a[100];
	for (int i = 0; i < n; i++)
	{
		a[i] = rand() % 1000;
	}
	cout << "The generated access process is:";
	for (int i = 0; i < n; i++)
	{
		if (i % 5 == 0)
		{
			cout << endl;
		}
		cout << a[i] << "  ";

	}
	cycle1:cout << "\n Please enter the starting location(0-200): ";
	cin >> m;
	cycle2:cout << "Please enter the disk scheduling method(1:FIFS   2:SSTF   3:SCAN)" << endl;
	cin >> flag;
	switch (flag)
	{
	case 1:
		cout << "implement FIFS algorithm" << endl; disk.FIFS(a, m, n); cout << "\n\n"; break;
	case 2:
		cout << "implement SSTF algorithm" << endl; disk.SSTF(a, m, n); cout << "\n\n"; break;
	case 3:
		cout << "implement SCAN" << endl;
		cout << "Please determine the scanning direction (scan outwards:'right',Scan inward'left')";   
		cin >> direction;
		disk.SCAN(a, m, n, direction); cout << "\n\n"; break;
	}
	cout << "\n Do you want to continue?(1: continue    0: exit    2: Reset initial position";
	cin >> p;
	if (p == 1)
		goto cycle2;
	else if (p == 2)
	{
		goto cycle1;
	}
	else return 0;
}

4. Screenshot output experiment results

The following results are the experimental results when scanning from the 100 track number:

FIFO algorithm, time complexity O(n) seek length 515.9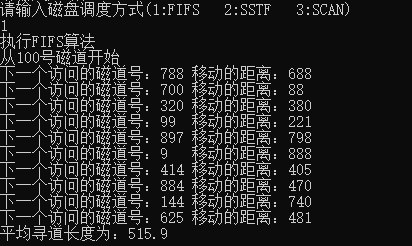

SSTF algorithm: time complexity O(n^2) average seek length 106.9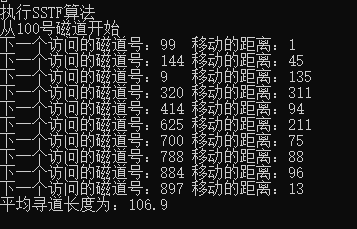

SCAN algorithm (SCAN out): time complexity O(n^2), average seek length: 168.5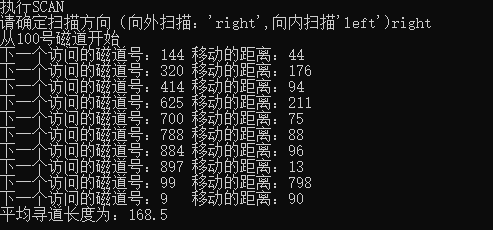

SCAN algorithm (inward scanning): time complexity O(n^2), average seek length: 97.9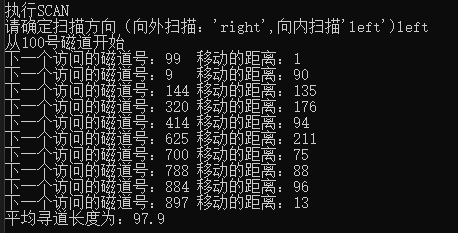

The following results are the experimental results when scanning from the 500 track number:

FIFS algorithm: time complexity is; O(n) average seek length is 515.9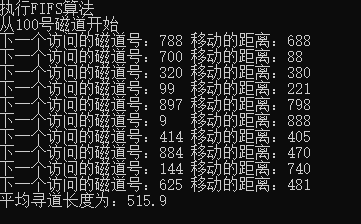

SSFT algorithm: time complexity is; O(n^2) average seek length is 106.9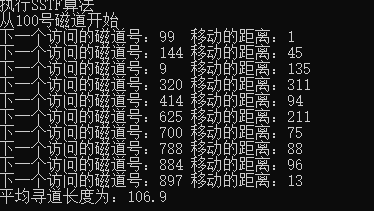

SCAN algorithm (outward): time complexity is; O(n^2) average seek length is 168.5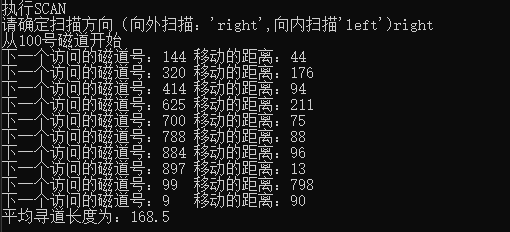

SCAN algorithm (inward): time complexity is; O(n^2) average seek length is 97.9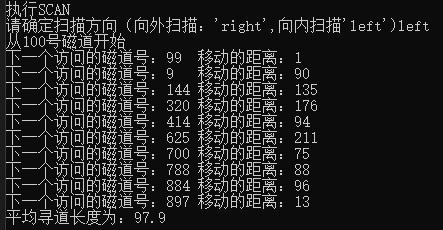

5. According to the experimental results and the principle of the theory class, the experimental analysis is carried out.

From the screenshot of the experimental results,
(1) For FIFS algorithm: the average seek length of FIFS algorithm is the longest when the initial position of track is in the position where the overall data is too small or too large. It can be seen that although the time complexity of FIFS algorithm is small, the average seek length is significantly higher than the other two algorithms, and the consumption of disk moving arm is more.
When the track initial position is in the middle of the whole data, the average seek length of FIFS algorithm is short. Because of the minimum time complexity and the relatively small consumption of disk moving arm, the algorithm can be used
(2) For SSTF algorithm: no matter where the track initial position is in the overall data, the average seek length changes relatively little and is relatively stable. For this data, it is stable at 106-137
(3) For SCAN algorithm,
1: When the initial position of the track is at the (larger / smaller) position of the overall data, the difference between the average seek length of SCAN algorithm and SCAN algorithm is large when they are accessed (outward / inward),
When it is in a small position, the average training length of outward access of the mobile arm is 168.5 (with 100 as the initial) and inward access is 97.9.
It can be seen that the result is opposite to that in the smaller position.
2: When the initial position of the track is in the middle of the whole data, the difference between the average seek length of the SCan algorithm and that of the SCan algorithm is small and relatively stable.

6, Thinking questions

1. By analyzing and comparing the time complexity of each algorithm, what is the efficiency of each algorithm?

According to the analysis of the above experimental results,
(1) The time complexity of FIFS is O(n) the lowest when the track initial position is larger or smaller than the overall access track data. The other two algorithms have O(n^2) time complexity, but the average seek length of FIFS is significantly higher than the other two algorithms, so they are abandoned.
When it is in a small position, the SCAN algorithm and SSTF algorithm can be used. In this case, the time complexity of the two algorithms is the same, and the average seek length is also close.
In the larger position, the opposite is true.
(2) When the initial position of the track is in the middle of the overall access track data, the FIFS algorithm has the least time complexity, and the average seek length is not much different from the other two algorithms, so the FIFS algorithm can be used
For the stability of the three algorithms:
FIFS>SCAN>SSTF

2. If all hard disks are designed as electronic hard disks, which disk scheduling algorithm is most suitable?

Because the speed of reading electronic hard disk is very fast and does not involve the problem of disk scheduling arm, the FIFS algorithm with the lowest time complexity should be used. The time complexity of the algorithm is: O(n);