target

In this chapter, we will recognize the handwritten dataset again, but use SVM instead of kNN.

Recognize handwritten numbers

In kNN, we directly use pixel intensity as feature vector. This time we will use the directional gradient histogram (HOG) as the feature vector.

Here, we use the second-order moment to correct the skew of the image before finding the HOG. Therefore, we first define a function deskew (), which takes a digital image and corrects it. Here is the deskew() function:

def deskew(img):
    m = cv.moments(img)
    if abs(m['mu02']) < 1e-2:
        return img.copy()
    skew = m['mu11']/m['mu02']
    M = np.float32([[1, skew, -0.5*SZ*skew], [0, 1, 0]])
    img = cv.warpAffine(img,M,(SZ, SZ),flags=affine_flags)
    return img

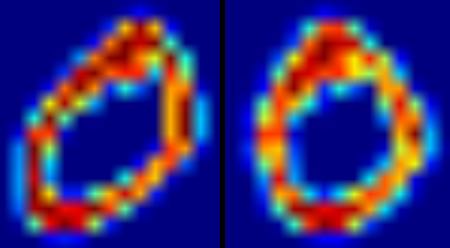
The following figure shows the up offset correction function applied to a zero image. The left image is the original image, and the right image is the offset corrected image.

Next, we have to find the HOG descriptor for each cell. For this reason, we find the Sobel derivatives of each element in the X and Y directions. Then find their size and gradient direction at each pixel. The gradient is quantized to 16 integer values. Divide the image into four sub squares. For each sub square, the histogram (16 bin) of weight size direction is calculated. So each sub square gives you a vector of 16 values. Four such vectors (of four sub squares) together provide us with a feature vector containing 64 values. This is the eigenvector we use to train the data.

def hog(img):
    gx = cv.Sobel(img, cv.CV_32F, 1, 0)
    gy = cv.Sobel(img, cv.CV_32F, 0, 1)
    mag, ang = cv.cartToPolar(gx, gy)
    bins = np.int32(bin_n*ang/(2*np.pi))    # quantizing binvalues in (0...16)
    bin_cells = bins[:10,:10], bins[10:,:10], bins[:10,10:], bins[10:,10:]
    mag_cells = mag[:10,:10], mag[10:,:10], mag[:10,10:], mag[10:,10:]
    hists = [np.bincount(b.ravel(), m.ravel(), bin_n) for b, m in zip(bin_cells, mag_cells)]
    hist = np.hstack(hists)     # hist is a 64 bit vector
    return hist

Finally, as before, we first split the big data set into individual cells. For each number, 250 units are reserved for training data and the remaining 250 are reserved for testing. The complete code is as follows, you can also download it from here:

#!/usr/bin/env python
import cv2 as cv
import numpy as np
SZ=20
bin_n = 16 # Number of bins
affine_flags = cv.WARP_INVERSE_MAP|cv.INTER_LINEAR
def deskew(img):
    m = cv.moments(img)
    if abs(m['mu02']) < 1e-2:
        return img.copy()
    skew = m['mu11']/m['mu02']
    M = np.float32([[1, skew, -0.5*SZ*skew], [0, 1, 0]])
    img = cv.warpAffine(img,M,(SZ, SZ),flags=affine_flags)
    return img
def hog(img):
    gx = cv.Sobel(img, cv.CV_32F, 1, 0)
    gy = cv.Sobel(img, cv.CV_32F, 0, 1)
    mag, ang = cv.cartToPolar(gx, gy)
    bins = np.int32(bin_n*ang/(2*np.pi))    # quantizing binvalues in (0...16)
    bin_cells = bins[:10,:10], bins[10:,:10], bins[:10,10:], bins[10:,10:]
    mag_cells = mag[:10,:10], mag[10:,:10], mag[:10,10:], mag[10:,10:]
    hists = [np.bincount(b.ravel(), m.ravel(), bin_n) for b, m in zip(bin_cells, mag_cells)]
    hist = np.hstack(hists)     # hist is a 64 bit vector
    return hist
img = cv.imread('digits.png',0)
if img is None:
    raise Exception("we need the digits.png image from samples/data here !")
cells = [np.hsplit(row,100) for row in np.vsplit(img,50)]
# First half is trainData, remaining is testData
train_cells = [ i[:50] for i in cells ]
test_cells = [ i[50:] for i in cells]
deskewed = [list(map(deskew,row)) for row in train_cells]
hogdata = [list(map(hog,row)) for row in deskewed]
trainData = np.float32(hogdata).reshape(-1,64)
responses = np.repeat(np.arange(10),250)[:,np.newaxis]
svm = cv.ml.SVM_create()
svm.setKernel(cv.ml.SVM_LINEAR)
svm.setType(cv.ml.SVM_C_SVC)
svm.setC(2.67)
svm.setGamma(5.383)
svm.train(trainData, cv.ml.ROW_SAMPLE, responses)
svm.save('svm_data.dat')
deskewed = [list(map(deskew,row)) for row in test_cells]
hogdata = [list(map(hog,row)) for row in deskewed]
testData = np.float32(hogdata).reshape(-1,bin_n*4)
result = svm.predict(testData)[1]
mask = result==responses
correct = np.count_nonzero(mask)
print(correct*100.0/result.size)

This special method gives us nearly 94% accuracy. You can try different values for various parameters of SVM to check whether higher precision can be achieved. Or, you can read technical papers about the field and try to implement them.

Additional resources

1. Histograms of Oriented Gradients Video: https://www.youtube.com/watch?v=0Zib1YEE4LU

Practice

1. The OpenCV example includes digits.py, which makes some improvements to the above methods to get improved results. It also contains references. Check and understand it.

Welcome to pioneer AI blog: http://panchuang.net/

OpenCV official document in Chinese: http://woshicver.com/

Welcome to pioneer blog Resource Hub: http://docs.panchuang.net/