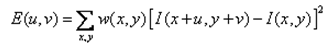(1) First, let's look at three pictures to understand what corner is:

We take a window as the center of a pixel in a picture. When the window moves in all directions, the change of its internal gray value is not obvious, then the point is in the flat area (such as the left image); when the change of its internal gray value is obvious only in several fixed directions, then the point is in the edge area (such as the middle part); when the window moves in all directions, the change is all. Obviously, the point is the corner (see right).

Of course, whether the changes mentioned above are obvious or not is compared with the threshold we set beforehand.

(2)moravec algorithm diagonal definition:

When the window moves in all directions, the gray value in the window will change greatly. But in the actual program, there are only eight directions in all directions. That is, the shape of the meter is 0, 45, 90, 135, 180, 225, 270 and 315 degrees.

For example:

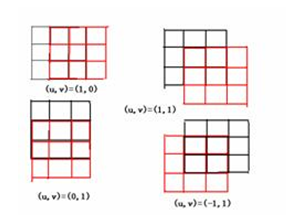
For the sake of simplicity, we only take four directions (0, 45, 90, 135 degrees). We take a square window of w*w (e.g. 5x5) to calculate the sum of squares of gray-scale differences in four directions: 0, 45, 90 and 135 degrees, and take the minimum value as the interest value of the pixel (as shown below).

Formula:  

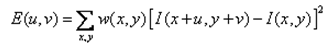
(3)moravec corner detection:

Steps:

<1> For each pixel, we calculate E(u,v). In our algorithm, (u,v) is ((1, 0), (1, 1), (0, 1), (-1, 1), (-1), where only four directions are taken.

minValue = min{E(u,v)} for each location corresponding to the minimum value calculated <2>.

Whether the minValue of each location is greater than the set threshold is determined by <3> and another process is to determine whether it is a local maximum to prevent duplication of corners?

Code:

1. #include <iostream>  
2. #include "cv.h"  
3. #include "highgui.h"  
4. #include "cxcore.h"  
5.   
6. using namespace std;  
7.   
8. int getMoravec(IplImage *src, CvSeq *corners, float threshold)  
9. {  
10.     int winSize = 5;  
11.     int y, x;  
12.     int halfwin = winSize/2;  
13.     int win;  
14.     IplImage *diffDst = cvCreateImage(cvGetSize(src), 32, 1);  //Keep the smallest variable value  
15.     int cornersCount = 0;   //Number of corners saved  
16.     for(y = halfwin; y < src->height - halfwin; y++)  
17.     {  
18.         for(x = halfwin; x < src->width - halfwin; x++)  
19.         {  
20.             float cornersResult[4];  
21.             cornersResult[0] = 0;  
22.             cornersResult[1] = 0;  
23.             cornersResult[2] = 0;  
24.             cornersResult[3] = 0;  
25.             float minValue;  
26.             for(win = -halfwin; win < halfwin; win++)  
27.             {  
28.                 cornersResult[0] += pow(cvGetReal2D(src, y, x+win) - cvGetReal2D(src, y, x+win+1), 2);  
29.                 cornersResult[1] += pow(cvGetReal2D(src, y+win, x+win) - cvGetReal2D(src, y+win+1, x+win+1), 2);  
30.                 cornersResult[2] += pow(cvGetReal2D(src, y+win, x) - cvGetReal2D(src, y+win+1, x), 2);  
31.                 cornersResult[3] += pow(cvGetReal2D(src, y+win, x-win) - cvGetReal2D(src, y+win+1, x-win-1),2);  
32.             }  
33.             minValue = cornersResult[0];  
34.             minValue = minValue < cornersResult[1] ? minValue : cornersResult[1];  
35.             minValue = minValue < cornersResult[2] ? minValue : cornersResult[2];  
36.             minValue = minValue < cornersResult[3] ? minValue : cornersResult[3];  
37.             cvSetReal2D(diffDst, y, x, minValue);  
38.         }  
39.     }  
40.     int yywin, xxwin, maxValue;  
41.     CvPoint resultLoc;  
42.     for(y = halfwin; y < src->height - halfwin; )  
43.     {  
44.         for(x = halfwin; x < src->width - halfwin;)  
45.         {     
46.             resultLoc.x = -1;  
47.             resultLoc.y = -1;  
48.             maxValue = 0;  
49.             for(yywin = -halfwin; yywin <= halfwin; yywin++)  
50.             {  
51.                 for(xxwin = -halfwin; xxwin < halfwin; xxwin++)  
52.                 {  
53.                     if(cvGetReal2D(diffDst, y+yywin, x+xxwin) > maxValue)  
54.                     {  
55.                         maxValue = cvGetReal2D(diffDst, y+yywin, x+xxwin);  
56.                         resultLoc.y = y+yywin;  
57.                         resultLoc.x = x+xxwin;   
58.                     }  
59.                 }  
60.             }  
61.             if(maxValue > threshold)  
62.             {  
63.                 cvSeqPush(corners, &resultLoc);    //Add corners. This function needs to remember *********  
64.                 cornersCount ++;  
65.             }  
66.             x += winSize;       //++ Multiple corners may occur  
67.         }  
68.         y += winSize;  
69.           
70.     }  
71.     cvReleaseImage(&diffDst);  
72.     return cornersCount;  
73. }  
74. int main()  
75. {  
76.     IplImage *src = cvLoadImage("E:\\study_opencv_video\\lesson17_1\\1.bmp", 0);  
77.     if(!src)  
78.     {  
79.         cout << "No Image loading..." << endl;  
80.         return 0;  
81.     }  
82.     CvSeq *corners;  
83.     CvMemStorage *mem = cvCreateMemStorage(0);  //Create a memory sequence. Space to save the final corner  
84.     corners = cvCreateSeq(0, sizeof(CvSeq), sizeof(CvPoint), mem);  //corners point to the memory sequence. corners will be saved in a CvSeq  
85.     float threshold =30000;  
86.     //Call functions to calculate corners  
87.     int cornersCount = getMoravec(src, corners, threshold);  
88.   
89.         //Extraction of Display Angle by Image show  
90.     IplImage* show= cvCreateImage(cvGetSize(src),8,3);  
91.     cvCvtColor(src,show,CV_GRAY2BGR);  
92.   
93.   
94.     //Get the coordinates of each corner point  
95.     for(int i = 0; i < cornersCount; i++)  
96.     {  
97.         //Draw a circle of half a kilogram and five centered on corner coordinates  
98.         CvPoint *pt = (CvPoint *)cvGetSeqElem(corners, i);  //And remember *********  
99.         cvCircle(show, *pt, 5, cvScalar(0,0,255));  
100.     }  
101.     cvNamedWindow("show");  
102.     cvShowImage("show", show);  
103.     cvWaitKey(0);  
104.     cvReleaseImage(&src);  
105.     cvReleaseImage(&show);  
106.     cvReleaseMemStorage(&mem);    //And remember this too ***  
107.     cvDestroyWindow("show");  
108.     return 0;  
109.   
110.   
111.   
112. }  

Added: Simply explain the cvSeq and cvMemStorage in the code. I am not too familiar with them. I took notes of them.

1. CvMemStorage *mem = cvCreateMemStorage(0);  //Create memory sequences  
2. CvSeq*corners = cvCreateSeq(0, sizeof(CvSeq), sizeof(CvPoint), mem);  //corners point to memory sequences  
3. cvSeqPush(corners, &resultLoc);    //Adding points to memory sequences  
4. CvPoint *pt = (CvPoint *)cvGetSeqElem(corners, i);  //Get the first element in seq  
5. cvReleaseMemStorage(&mem);   //Release memory sequence space  

1. cvSeqRemove(corners,i);  //Remove point i  

1. cvSeqSort(corners,cmpFunc,0);//Sort the points in the memory sequence  

1. //Comparison function for seq sorting  
2. static int cmpFunc(const void* _cur , const void* _next , void* userdata)  
3. {  
4.     PHARRISPOINT cur = (PHARRISPOINT)_cur;  
5.     PHARRISPOINT next = (PHARRISPOINT)_next;  
6.   
7.     return cur->cornerness < next->cornerness ? 1 : -1;  
8. }  

(4) Disadvantage of Moravec corner detection

moravec corner detection has two main shortcomings:

1. No rotation invariance

2. Strong response to edge points

Author: Villager from: http://blog.csdn.net/lu597203933 Reprint or share are welcome, but be sure to state the source of the article. (Sina Weibo: small village leader zack, welcome to exchange!)