edge detection
1, Understanding of edge detection
Edge generally refers to the region where the intensity of an image changes sharply in a certain part. There are generally two situations of strength change:
Step change:
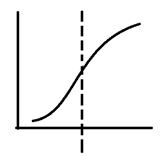
The image value changes from low to high, and the image changes from dark to bright
Peak change:
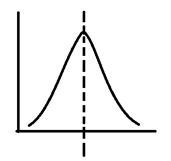
From dark to light and then to dark, both sides are dark and the center is prominent.
Edge detection is actually to find a set of two intensity changes.
Since the edge is the position with the most drastic gray change, the most intuitive idea is to calculate the difference (the difference between adjacent pixels).
The difference method for edge detection must make the direction of difference perpendicular to the direction of edge, which requires differential operation in different directions of image, which increases the amount of operation. Generally, the edge can be divided into horizontal edge, vertical edge and diagonal edge.
For the first case, the peak of the first-order difference is the edge point, and the zero of the second-order difference is the edge point.
For the second case, the zero of the first-order difference is the edge point, and the peak of the second-order difference is the edge point.
2, Common edge detection operators
1. Normal gradient operator:
The ordinary gradient operator is also called orthogonal gradient operator, which calculates the gradient between the top of the pixel and the pixel and the gradient between the left of the pixel and the pixel respectively.
D x ( m , n ) = f ( m , n ) − f ( m − 1 , n ) Dx\left(m,n\right)=f\left(m,n\right)-f\left(m-1,n\right) Dx(m,n)=f(m,n)−f(m−1,n)
D y ( m , n ) = f ( m , n ) − f ( m , n − 1 ) Dy\left(m,n\right)=f\left(m,n\right)-f\left(m,n-1\right) Dy(m,n)=f(m,n)−f(m,n−1)
D ( m , n ) = ( D x 2 + D y 2 ) D\left(m,n\right)=\sqrt{\left(Dx^2+Dy^2\right)} D(m,n)=(Dx2+Dy2)
Left operator:
[
0
0
−
1
1
]
\left[\begin{matrix}\\0&0\\-1&1\\\end{matrix}\right]
[0−101]
Upper operator:
[ 0 − 1 0 1 ] \left[\begin{matrix}\\0&-1\\0&1\\\end{matrix}\right] [00−11]
2. Roberts operator:
The Roberts operator is similar to the ordinary gradient operator, taking the first-order difference as the gradient. The difference lies in the position of the value:
D x ( m , n ) = f ( m , n ) − f ( m − 1 , n − 1 ) Dx\left(m,n\right)=f\left(m,n\right)-f\left(m-1,n-1\right) Dx(m,n)=f(m,n)−f(m−1,n−1)
D y ( m , n ) = f ( m − 1 , n ) − f ( m , n − 1 ) Dy\left(m,n\right)=f\left(m-1,n\right)-f\left(m,n-1\right) Dy(m,n)=f(m−1,n)−f(m,n−1)
D
(
m
,
n
)
=
(
D
x
2
+
D
y
2
)
D\left(m,n\right)=\sqrt{\left(Dx^2+Dy^2\right)}
D(m,n)=(Dx2+Dy2)
Positive diagonal operator:
[
−
1
0
0
1
]
\left[\begin{matrix}\\-1&0\\0&1\\\end{matrix}\right]
[−1001]
Diagonal operator:
[
0
1
−
1
0
]
\left[\begin{matrix}\\0&1\\-1&0\\\end{matrix}\right]
[0−110]
3. Prewitt operator:
Prewitt combines the idea of difference and neighborhood average, and its convolution kernel is as follows
Horizontal convolution kernel:
1
3
∗
[
−
1
0
1
−
1
0
1
−
1
0
1
]
\frac{1}{3}*\left[\begin{matrix}-1&0&1\\-1&0&1\\-1&0&1\\\end{matrix}\right]
31∗⎣⎡−1−1−1000111⎦⎤
Vertical convolution kernel:
1 3 ∗ [ − 1 − 1 − 1 0 0 0 1 1 1 ] \frac{1}{3}*\left[\begin{matrix}-1&-1&-1\\ 0&0&0\\1&1&1\\\end{matrix}\right] 31∗⎣⎡−101−101−101⎦⎤
4. Sobel operator:
Sobel operator adds the idea of weight on the basis of Prewitt operator. The closer to the pixel, the higher the weight.
Horizontal convolution kernel:
1
5
∗
[
−
1
0
1
−
2
0
2
−
1
0
1
]
\frac{1}{5}*\left[\begin{matrix}-1&0&1\\ -2&0&2\\-1&0&1\\\end{matrix}\right]
51∗⎣⎡−1−2−1000121⎦⎤
Vertical convolution kernel:
1 5 ∗ [ − 1 − 2 − 1 0 0 0 1 2 1 ] \frac{1}{5}*\left[\begin{matrix}-1&-2&-1\\ 0&0&0\\1&2&1\\\end{matrix}\right] 51∗⎣⎡−101−202−101⎦⎤
5. Laplacian:
(a little lazy, using the previous blog (- -))
Laplace transform is an integral transform commonly used in engineering mathematics;
Laplace operator is a second-order differential operator in n-dimensional Euclidean space;
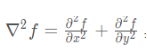
With isotropy, the first derivative of digital image is:
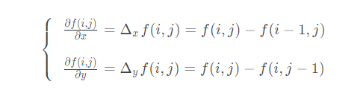
The second derivative is:
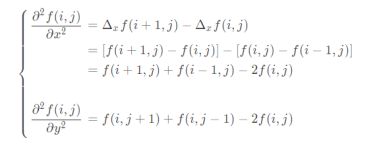
So the Laplace operator is:
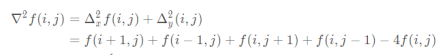
The four neighborhood template of Laplace operator is as follows:
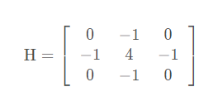
Eight neighborhoods:
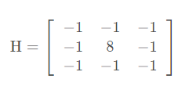
Illustration of convolution:
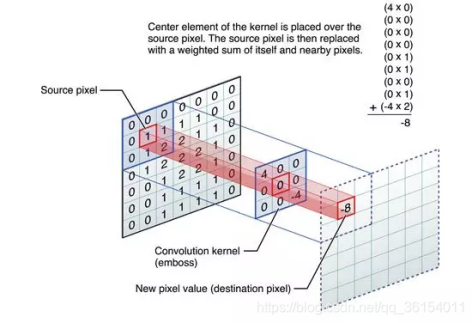
Then, by sliding the convolution kernel, the convolution result of the whole picture can be obtained.
6. LoG Operator:
The full name is Laplacian of Gaussian, which is the Gaussian Laplacian operator. The principle is the second-order differentiation of the Gaussian distribution formula
The Gaussian function is:
G
σ
(
x
,
y
)
=
1
2
π
σ
2
exp
(
−
x
2
+
y
2
2
σ
2
)
G_{\sigma}(x, y)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp \left(-\frac{x^{2}+y^{2}}{2 \sigma^{2}}\right)
Gσ(x,y)=2πσ2
1exp(−2σ2x2+y2)
The quadratic partial derivative is obtained:
L
o
G
≜
Δ
G
σ
(
x
,
y
)
=
∂
2
∂
x
2
G
σ
(
x
,
y
)
+
∂
2
∂
y
2
G
σ
(
x
,
y
)
=
x
2
+
y
2
−
2
σ
2
σ
4
e
−
(
x
2
+
y
2
)
/
2
σ
2
L o G \triangleq \Delta G_{\sigma}(x, y)=\frac{\partial^{2}}{\partial x^{2}} G_{\sigma}(x, y)+\frac{\partial^{2}}{\partial y^{2}} G_{\sigma}(x, y)=\frac{x^{2}+y^{2}-2 \sigma^{2}}{\sigma^{4}} e^{-\left(x^{2}+y^{2}\right) / 2 \sigma^{2}}
LoG≜ΔGσ(x,y)=∂x2∂2Gσ(x,y)+∂y2∂2Gσ(x,y)=σ4x2+y2−2σ2e−(x2+y2)/2σ2
The direct construction of convolution template has large amount of calculation and low efficiency,
Therefore, the approximate method is generally adopted, and the approximate 5x5 LOG operator is commonly used:
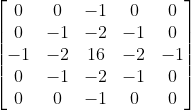
7. Canny operator:
Canny operator is divided into four steps: image denoising, calculating image gradient, non maximum suppression and threshold screening
1. Image noise reduction
Gradient operator is essentially an operator describing the prominent value of image gray, so it is greatly affected by noise. Because the noise is represented as prominent abnormal data points, noise reduction is required in the first step, generally using Gaussian filter;
2. Calculate image gradient
Calculating the image gradient can get the edge of the image, because the gradient is where the gray change is obvious, and the edge is also where the gray change is obvious. Of course, this step can only get the possible edge. Because where the gray level changes may or may not be the edge. In this step, there is a set of all possible edges.
Sobel operator is used as gradient operator by default in OpenCV.
3. Non maximum suppression
Generally, the gray changes are concentrated in the gradient direction in the local range,
The largest gray change is retained, and the others are not retained, which can eliminate most of the points.
Turn an edge with multiple pixels wide into a single pixel wide edge.
The main purpose of this step is thin edge, which needs to be judged by combining gradient direction and gradient value;
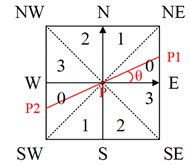
The gradient is divided into 8 directions, namely E, NE, N, NW, W, SW, S and Se (which are actually pixels),
Where 0 represents 0 to 45 degrees, 1 represents 45 to 90 degrees, 2 represents - 90 to - 45 degrees, and 3 represents - 45 to 0 degrees.
The gradient direction of pixel P is θ \theta θ, Then the gradient linear interpolation of pixel points P1 and P2 is:
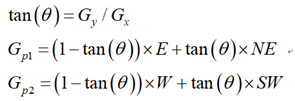
Then the pseudo code of non maximum suppression is:
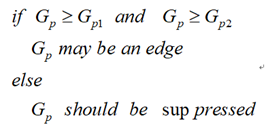
4. Threshold filtering
After non maximum suppression, there are still many possible edge points,
Further, a double threshold is set, that is, low threshold and high threshold.
If the gray change is greater than high, it is set as strong edge pixels. If it is lower than low, it is eliminated.
The between low and high is set to weak edge.
It is further judged that if there are strong edge pixels in its field, it shall be retained, and if not, it shall be eliminated.
OpenCV has two functions:
The first is to input two different mutually orthogonal gradient maps:
CV_EXPORTS_W void Canny( InputArray dx, InputArray dy,
OutputArray edges,
double threshold1, double threshold2,
bool L2gradient = false );
InputArray dx: gradient operator in x direction, such as x operator of sobel operator;
InputArray dx: gradient operator in Y direction, such as y operator of sobel operator;
double threshold1, the minimum threshold. If it is less than this threshold, it is not an edge;
double threshold2, the maximum threshold. If it is greater than this threshold, it is a strong edge;
The second input is an 8-bit grayscale image
CV_EXPORTS_W void Canny( InputArray image, OutputArray edges,
double threshold1, double threshold2,
int apertureSize = 3, bool L2gradient = false );
The default gradient operator is Sobel operator
apertureSize is the size of Sobel operator
3, Results
Ordinary gradient operator (not obvious):

roberts operator:

prewiit operator:

sobel operator:

Laplacian:

LoG Operator:

Canny operator (simple suppression of non maxima):

Canny operator in OpenCV (interpolation suppression):

4, Code
#include <opencv.hpp>
using namespace std;
using namespace cv;
void Grad(Mat src_gradient,Mat& dst);
void Roberts(Mat src_roberts, Mat& dst);
void Prewiit(Mat src_Prewiit, Mat& dst);
void Sobel(Mat src_sobel, Mat& dst);
void Laplacian(Mat src_lap, Mat& dst);
void LapofGaussi(Mat src_log, Mat& dst, int size,double sigma);
void Canny(Mat src_canny, Mat& dst, int value_low, int value_high);
void main()
{
Mat src = imread("test.jpg");
//Seven common edge detection algorithms
Mat gray,gradient, roberts, prewiit, sobel, laplacian, LoG, canny,cv_canny;
Grad(src, gradient);
Roberts(src, roberts);
Prewiit(src, prewiit);
Sobel(src, sobel);
Laplacian(src, laplacian);
LapofGaussi(src, LoG,5,1.0);
Canny(src, canny, 10,100);
cvtColor(src, gray, COLOR_BGR2GRAY);
cv::Canny(gray, cv_canny, 10, 100);
imshow("src", src);
imshow("gradient", gradient);
imshow("prewiit", prewiit);
imshow("roberts", roberts);
imshow("sobel", sobel);
imshow("laplacian", laplacian);
imshow("canny", canny);
imshow("cv_canny", cv_canny);
imshow("LoG", LoG);
waitKey(0);
}
//General gradient method
void Grad(Mat src_gradient, Mat& dst)
{
Mat gauss,gray;
GaussianBlur(src_gradient, gauss, Size(3, 3), 0.8, 0.8);
cvtColor(gauss, gray, COLOR_BGR2GRAY);
Mat dst_x, dst_y;
Mat out(Size(gray.size()), gray.type());
dst = out;
Mat kernel_x = (Mat_<double>(2, 2) << 0, 0, -1, 1);
Mat kernel_y = (Mat_<double>(2, 2) << 0, -1, 0, 1);
filter2D(gray, dst_x, -1, kernel_x);
filter2D(gray, dst_y, -1, kernel_y);
double s = 0.0;
int n = gray.cols*gray.rows;
for (int i = 0 ;i<src_gradient.rows;i++)
{
uchar* ptr_x = dst_x.ptr<uchar>(i);
uchar* ptr_y = dst_y.ptr<uchar>(i);
uchar* ptr_dst = dst.ptr<uchar>(i);
for (int j = 0; j < src_gradient.cols; j++)
{
ptr_dst[j] = sqrt(ptr_x[j]* ptr_x[j] + ptr_y[j]* ptr_y[j]);
s += ptr_dst[j];
}
}
s = s / n;
// for (int i = 0; i < src_gradient.rows; i++)
// {
// for (int j = 0; j < src_gradient.cols; j++)
// {
// if (dst.at<uchar>(i, j) >= s)
// {
// dst.at<uchar>(i, j) = 255;
// }
//
// }
//
// }
}
void Roberts(Mat src_roberts, Mat & dst)
{
Mat gauss, gray;
GaussianBlur(src_roberts, gauss, Size(3, 3), 0.8, 0.8);
cvtColor(src_roberts, gray, COLOR_BGR2GRAY);
Mat dst_x, dst_y;
Mat out(Size(gray.size()), gray.type());
dst = out;
Mat kernel_x = (Mat_<double>(2, 2) << -1, 0, 0, 1);
Mat kernel_y = (Mat_<double>(2, 2) << 0, -1, 1, 0);
filter2D(gray, dst_x, -1, kernel_x);
filter2D(gray, dst_y, -1, kernel_y);
double s = 0.0;
int n = src_roberts.cols*src_roberts.rows;
for (int i = 0; i < src_roberts.rows; i++)
{
uchar* ptr_x = dst_x.ptr<uchar>(i);
uchar* ptr_y = dst_y.ptr<uchar>(i);
uchar* ptr_dst = dst.ptr<uchar>(i);
for (int j = 0; j < src_roberts.cols; j++)
{
ptr_dst[j] = sqrt(ptr_x[j] * ptr_x[j] + ptr_y[j] * ptr_y[j]);
s += ptr_dst[j];
}
}
s = s / n;
// for (int i = 0; i < src_roberts.rows; i++)
// {
// for (int j = 0; j < src_roberts.cols; j++)
// {
// if (dst.at<uchar>(i,j)>=s)
// {
// dst.at<uchar>(i, j) = 255;
// }
//
// }
//
// }
}
void Prewiit(Mat src_Prewiit, Mat & dst)
{
Mat gauss, gray;
GaussianBlur(src_Prewiit, gauss, Size(3, 3), 0.8, 0.8);
cvtColor(gauss, gray, COLOR_BGR2GRAY);
Mat dst_x, dst_y;
Mat out(Size(gray.size()), gray.type());
dst = out;
Mat kernel_x = (Mat_<double>(3, 3) << 1.0/3, 0, -1.0/3, 1.0 / 3, 0, -1.0 / 3, 1.0 / 3, 0, -1.0 / 3);
Mat kernel_y = (Mat_<double>(3, 3) << 1.0 / 3, 1.0/3, 1.0 / 3,0,0,0, -1.0 / 3, -1.0 / 3, -1.0 / 3);
filter2D(gray, dst_x, -1, kernel_x);
filter2D(gray, dst_y, -1, kernel_y);
double s = 0.0;
int n = gray.cols*gray.rows;
for (int i = 0; i < src_Prewiit.rows; i++)
{
uchar* ptr_x = dst_x.ptr<uchar>(i);
uchar* ptr_y = dst_y.ptr<uchar>(i);
uchar* ptr_dst = dst.ptr<uchar>(i);
for (int j = 0; j < src_Prewiit.cols; j++)
{
ptr_dst[j] = sqrt(ptr_x[j] * ptr_x[j] + ptr_y[j] * ptr_y[j]);
s += ptr_dst[j];
}
}
s = s / n;
// for (int i = 0; i < src_Prewiit.rows; i++)
// {
// for (int j = 0; j < src_Prewiit.cols; j++)
// {
// if (dst.at<uchar>(i, j) >= s)
// {
// dst.at<uchar>(i, j) = 255;
// }
//
// }
//
// }
}
void Sobel(Mat src_sobel, Mat & dst)
{
Mat gauss, gray;
GaussianBlur(src_sobel, gauss, Size(3, 3), 0.8, 0.8);
cvtColor(gauss, gray, COLOR_BGR2GRAY);
Mat dst_x, dst_y;
Mat out(Size(gray.size()), gray.type());
dst = out;
Mat kernel_x = (Mat_<double>(3, 3) << 1.0 / 5, 0, -1.0 / 3, 2.0 / 5, 0, -2.0 / 5, 1.0 / 3, 0, -1.0 / 3);
Mat kernel_y = (Mat_<double>(3, 3) << 1.0 / 5, 2.0 / 5, 1.0 / 5, 0, 0, 0, -1.0 / 5, -2.0 / 5, -1.0 / 5);
filter2D(gray, dst_x, -1, kernel_x);
filter2D(gray, dst_y, -1, kernel_y);
double s = 0.0;
int n = gray.cols*gray.rows;
for (int i = 0; i < src_sobel.rows; i++)
{
uchar* ptr_x = dst_x.ptr<uchar>(i);
uchar* ptr_y = dst_y.ptr<uchar>(i);
uchar* ptr_dst = dst.ptr<uchar>(i);
for (int j = 0; j < src_sobel.cols; j++)
{
ptr_dst[j] = sqrt(ptr_x[j] * ptr_x[j] + ptr_y[j] * ptr_y[j]);
s += ptr_dst[j];
}
}
s = s / n;
// for (int i = 0; i < src_sobel.rows; i++)
// {
// for (int j = 0; j < src_sobel.cols; j++)
// {
// if (dst.at<uchar>(i, j) >= s)
// {
// dst.at<uchar>(i, j) = 255;
// }
//
// }
//
// }
}
void Laplacian(Mat src_lap, Mat & dst)
{
Mat gauss, gray;
GaussianBlur(src_lap, gauss, Size(3, 3), 0.8, 0.8);
cvtColor(gauss, gray, COLOR_BGR2GRAY);
Mat kernel = (Mat_<double>(3, 3) << 0, -1.0, 0, -1.0, 4, -1.0,0, -1.0, 0);
filter2D(gray, dst, -1, kernel);
double s = 0.0;
double n = gray.cols*gray.rows/4;
for (int i = 0; i < src_lap.rows; i++)
{
uchar* ptr_dst = dst.ptr<uchar>(i);
for (int j = 0; j < src_lap.cols; j++)
{
s += ptr_dst[j];
}
}
s = s / n;
for (int i = 0; i < src_lap.rows; i++)
{
for (int j = 0; j < src_lap.cols; j++)
{
if (dst.at<uchar>(i, j) >= s)
{
dst.at<uchar>(i, j) = 255;
}
}
}
}
void LapofGaussi(Mat src_log, Mat & dst,int size, double sigma)
{
Mat gauss, gray;
GaussianBlur(src_log, gauss, Size(3, 3), 0.8, 0.8);
cvtColor(gauss, gray, COLOR_BGR2GRAY);
double N = (size - 1) / 2;
double C = -1.0 / (CV_PI*pow(sigma,4));
Mat kernel = (Mat_<double>(5, 5) << -2, -4, -4, -4, -2,
-4, 0, 8, 0, -4,
-4, 8, 24, 8, -4,
-4, 0, 8, 0, -4,
-2, -4, -4, -4, -2);
// double theta = 0.0;
// for (int y = 0;y<size;y++)
// {
// double* ptr = kernel.ptr<double>(y);
//
// for (int x = 0; x < size; x++)
// {
//
// ptr[x] = C*(1.0- (pow((double)x - N, 2) + pow((double)y - N, 2)) / 2.0*sigma*sigma)*exp(-(pow((double)x - N, 2) + pow((double)y - N, 2))/2.0*sigma*sigma);
// theta += ptr[x];
//
//
// }
//
//
// }
// for (int y = 0; y < size; y++)
// {
// double* ptr = kernel.ptr<double>(y);
//
// for (int x = 0; x < size; x++)
// {
//
// ptr[x] /= theta;
//
//
//
// }
//
//
// }
filter2D(gray, dst, -1, kernel);
}
void Canny(Mat src_canny, Mat & dst_canny,int value_low,int value_high)
{
Mat gauss, gray,dst;
//Step 1 noise processing
GaussianBlur(src_canny, gauss, Size(3, 3), 1, 1);
cvtColor(gauss, gray, COLOR_BGR2GRAY);
Mat dst_x(src_canny.rows,src_canny.cols,CV_32FC1), dst_y(src_canny.rows, src_canny.cols, CV_32FC1);
Mat out(Size(gray.size()), gray.type());
dst = out;
dst_canny = cv::Mat::zeros(src_canny.rows,src_canny.cols,CV_8UC1);
//The second step is Sobel operator to detect the edge
Mat kernel_x = (Mat_<double>(3, 3) << 1.0 / 5, 0, -1.0 / 3, 2.0 / 5, 0, -2.0 / 5, 1.0 / 3, 0, -1.0 / 3);
Mat kernel_y = (Mat_<double>(3, 3) << 1.0 / 5, 2.0 / 5, 1.0 / 5, 0, 0, 0, -1.0 / 5, -2.0 / 5, -1.0 / 5);
filter2D(gray, dst_x, -1, kernel_x);
filter2D(gray, dst_y, -1, kernel_y);
for (int i = 0; i < src_canny.rows; i++)
{
uchar* ptr_x = dst_x.ptr<uchar>(i);
uchar* ptr_y = dst_y.ptr<uchar>(i);
uchar* ptr_dst = dst.ptr<uchar>(i);
for (int j = 0; j < src_canny.cols; j++)
{
ptr_dst[j] = sqrt(ptr_x[j] * ptr_x[j] + ptr_y[j] * ptr_y[j]);
}
}
dst_x.convertTo(dst_x, CV_32FC1, 1.0 / 255);
dst_y.convertTo(dst_y, CV_32FC1, 1.0 / 255);
Mat mag, angle;
//Calculate gradient amplitude and gradient direction
//The polar coordinate function can calculate r and theta
cartToPolar(dst_x, dst_y, mag, angle, 1);
for (int i = 0; i < src_canny.rows; i++)
{
for (int j = 0; j < src_canny.cols; j++)
{
double value = angle.at<float>(i, j);
if ((value <= 22.5 && value> -22.5) || (value >= 157.5 && value < -157.5))
{
angle.at<float>(i, j) = 0;//0 degrees
}
if ((value <= 67.5 && value > 22.5) || (value < -112.5 && value >= -157.5))
{
angle.at<float>(i, j) = 45;//45 degrees
}
if ((value > 67.5 && value <= 112.5) || (value < -67.5 && value >= -112.5))
{
angle.at<float>(i, j) = 90;//90 degrees
}
if ((value > 112.5 && value < 157.5) || (value < -112.5 && value >= -157.5))
{
angle.at<float>(i, j) = 135;//135 degrees
}
}
}
//The non maximum suppression of four gradient directions is briefly discussed
for (int i = 1; i < src_canny.rows-1; i++)
{
for (int j = 1; j < src_canny.cols-1; j++)
{
uchar t = dst.at<uchar>(i, j);
uchar a = dst.at<uchar>(i-1, j);
uchar b = dst.at<uchar>(i+1, j);
uchar c = dst.at<uchar>(i, j-1);
uchar d = dst.at<uchar>(i, j+1);
uchar e = dst.at<uchar>(i + 1, j+1);
uchar f = dst.at<uchar>(i - 1, j - 1);
uchar g = dst.at<uchar>(i - 1, j + 1);
uchar h = dst.at<uchar>(i + 1, j - 1);
double value = angle.at<float>(i, j);
if (dst.at<uchar>(i, j) <= value_low)
{
dst_canny.at<uchar>(i, j) = 0;
}
// if (dst.at<uchar>(i, j) >= value_low )
// {
// If (DST. At < uchar > (I, J) < = value_high) / / weak edge
// {
if (value == 135 && t == std::max(std::max(t, g), h))//The gradient direction is 135 degrees
{
dst_canny.at<uchar>(i,j) = t;
}
if (value == 90 && t == std::max(std::max(t, a), b))//The gradient direction is 90 degrees
{
dst_canny.at<uchar>(i, j) = t;
}
if (value == 45 && t == std::max(std::max(t, e), f))//The gradient direction is 45 degrees
{
dst_canny.at<uchar>(i, j) = t;
}
if (value == 0 && t == std::max(std::max(t, c), d))//The gradient direction is 0 degrees
{
dst_canny.at<uchar>(i, j) = t;
}
/*}*/
/*}*/
}
}
//There is a problem with double threshold processing
for (int i = 0 ; i< src_canny.rows;i++)
{
for (int j = 0; j < src_canny.cols; j++)
{
uchar t = dst.at<uchar>(i, j);
if (dst_canny.at<uchar>(i, j) >= value_low)
{
dst_canny.at<uchar>(i, j) = 255;
// If (dst_canny. At < uchar > (I, J) > = value_high) / / strong edge
// {
//
// for (int n = 3 ;n > 0 ;n--)
// {
// for (int m = 3; m > 0; m--)
// {
// if ((i > 0 && j > 0) && (i <src_canny.rows-1 && j<src_canny.cols-1))
// {
//
// uchar k = dst_canny.at<uchar>(i - n + 2, j - m + 2);
// if (k >= 0 && k < value_high)
// {
// dst_canny.at<uchar>(i - n + 2, j - m + 2) = 255;
// }
// }
// }
//
// }
//
// }
// // If (dst_canny. At < uchar > (I, J) < = value_high) / / weak edge
// // {
// // dst_canny.at<uchar>(i, j) = 127;
// //
// // }
}
else
{
dst_canny.at<uchar>(i, j) = 0;
}
}
}
}