Source: http://blog.csdn.net/songzitea/article/details/13614977
Background introduction
The main content of this section comes from the introduction of Trajkovic operator by Miroslav Trajkovic and Mark Hedley[1] in 1998. FastCorner
Detection . Trajkovic Operator
(4-Neighbours) [3] (Note: The pictures in this section are mainly from here). The value of Trajkovic operator corner extraction method is that it is better than other corner extraction methods in the same period (such as Moravec corner, Harris corner). At the same time, it is much faster than other corner extraction methods in the same period.
fundamental theory
The definition of the author's diagonal point is the same as that of Moravec's and Harris's: the point where the gray value of the image varies greatly in all directions is regarded as the corner point. The definition of corner quantity is similar to Moravec, that is, the minimum value of gray level change in each direction (when the change of gray level is the smallest in a certain direction and the minimum value is larger than a certain threshold, then this point is considered as a corner point). And Moravec Trajkovic performs better than harris, because Trajkovic uses pixel interpolation to compare the degree of gray value change in each direction, while moravec only compares in a limited direction. Compared with harris, both have the same effect, but Trajkovic is much faster than haris.
Trajkovic's performance in speed determines that it can be used in systems with high real-time requirements. But Trajkovic also has the disadvantage that it does not have rotation invariance, is sensitive to noise, and has a large response value to diagonal points. There will be corresponding methods for these shortcomings, but these shortcomings can not be completely solved. Trajkovic operator calculates the angular points in a small circular window, and considers all the straight lines passing through the center of the circle, that is, calculates the degree of gray value change in each possible direction. Assuming that the center of a circle is represented by C, any straight line passing through the center of the circle will intersect the circle at two points, as shown in Figure 1.

Figure 1: Notation for Trajkovic Operator
So, the definition of Trajkovic's diagonal quantity is
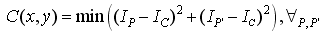
C(x,y) denotes the amount of corners at any point (x,y) on image I. This formula can tell whether it is a corner or not. There are four cases in which point (x,y) is located at the destination of the image. As shown in the following figure:
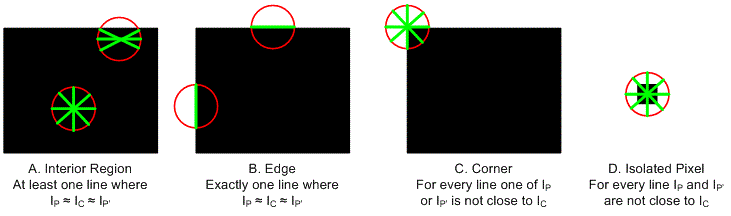
The first case: point (x,y) in the internal area: at this time, the circular window through the center of point (x,y) is completely in a relatively flat area, or most of the circular windows are in this flat area (as shown in figure A above). In this case, at least one large straight line passing through the center point C makes the Ic equal to Ip and Ic equal to Ip'. According to the formula for calculating corners, the calculated C(x,y) must be a very small value, so that the point (x,y) can be excluded from the corners. Moreover, in most cases, there will be more than one such point P memory, making noise tolerance to a certain extent.
Second case: point (x,y) on the edge: at this time, the center point (x,y) of the circular window just falls on the edge (as shown in figure B above). There is only one point to P,P'makes Ic approximately equal to Ip and Ic approximately equal to Ip'. Under ideal conditions, the angular quantity C(x,y) calculated from the formula of angular quantity is relatively small. But because there is only one straight line like this, it is easy to be disturbed by noise.
Third case: point (x,y) at the corner: when the center of the circular window (x,y) is at the corner (as shown in figure C above). The gray value of at least one point in any point (x,y) intersecting with a circle P, P', P'differs greatly from that of the central point. So the calculated corners are larger (larger than the set threshold, so they will be considered corners).
Fourth case: point (x,y) at an isolated point: if at an isolated point (as shown in figure D above), for each line Ip, Ip', the difference between the score and the value of Ic is large, then the calculated corners are also large. This point is noisy at this point, but because of the large amount of corners, it will be considered as corners. In order to eliminate the influence of this kind of noise, we can first use Gauss smoothing to denoise.
According to the above analysis, Trajkovic is greatly affected by noise, so it is possible to realize Gauss smoothing denoising before corner detection using Trajkovic operator.
Calculating Method of Corner Quantity
At present, there is no specific introduction about how to calculate the corner quantity of Trajkovic. Firstly, as shown in Figure 2 below, the horizontal gray value variation rA and the vertical gray value variation rB are easy to calculate.
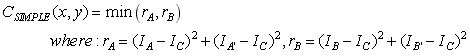
How to calculate the change degree of gray value in any direction? First of all, we can take the minimum value of the corners:
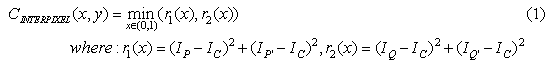
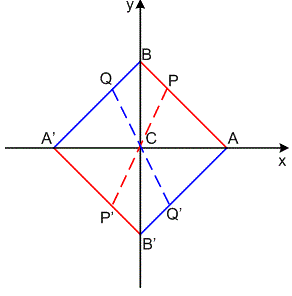
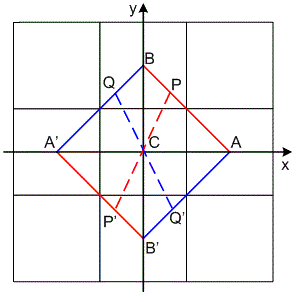
Figure 2: Interpixel positions Figure3: Interpixel approximation for a 3x3 window using 4-neighbours
Now, we can convert the problem into that any line passing through point C intersects with a circle at P, P', Q':

Substitute Formula (2) into Formula (1):
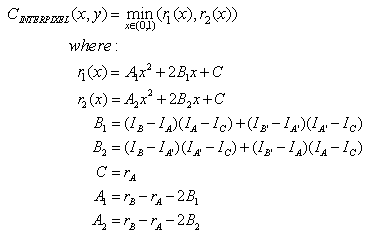
Well, The minimum is the conclusion that
The minimum is the conclusion that
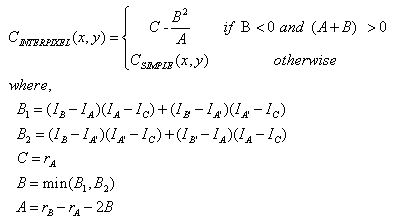
Multigrid Algorithm
Corners can be divided into two categories: geometric corners and texture corners. Geometric corners are intersected by the edges of objects in the image. The texture corners are generated by the texture of the object surface (such as grass, clothing texture, etc.). Usually, the number of geometric corners in an image is much less than that of texture corners. The aim of multi-lattice algorithm is to detect more geometric corners and less texture points. Trajkovic believes that geometric corners are more stable than texture corners. Therefore, from the point of view of practical use, it is reasonable to reduce texture corners.
After observation, it is found that the texture corners are generally very dense, and the gray value changes in a very small area. Therefore, the transformation of gray value in the region can be eliminated by reducing the original image and then extracting the corners. The method of image reduction is not interpolation, but averaging. As shown in the following figure:
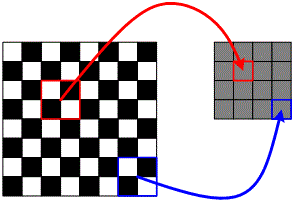
In Trajkovic corner detection, firstly, the original image is reduced by using multi-grid method, which not only reduces the number of texture corner points detected, but also speeds up the speed of Trajkovic corner detection. In the reduced version of Trajkovic corner detection image, a simple corner calculation formula is used to preliminarily determine whether the candidate corner points are or not. If so, it is further determined on the original image.

Figure 4: Corner points detected at different image resolutions
As shown in Figure 4, the original size is 256*256. There is a grassland in the image, and the corners on the grassland are meaningless for us to match corners. When the image was reduced to 128*128, the corners on the grassland were eliminated. Of course, the image can not be reduced too much, otherwise, the geometric corners will disappear, when reduced to 64*64, part of the geometric corners will disappear.
Algorithm flow



Code:
English Links: http://kiwi.cs.dal.ca/~dparks/CornerDetection/trajkovic.htm