Next one.

Look at the function

The first parameter and the second parameter are similar to the previous one, but the last one is about multiple sets of points in multiple graphs. The type is double vector. Here is a set of points in a pair of graphs, the type is single vector.

vector<Point3f> calcBoardCornerPositions(int gridW, int gridH, float squareSize)
{
    vector<Point3f> objectPoints;
        for (int i = 0; i < gridH; i++)
            for (int j = 0; j < gridW; j++)
                objectPoints.push_back(Point3f(float(j*squareSize), float(i*squareSize), 0));
    return objectPoints;
}
            vector<Point3f> objectPoints = calcBoardCornerPositions(grids.width, grids.height);

Second parameter

        vector<Point2f> corners;
        bool found = findChessboardCorners(images, grids, corners, CALIB_CB_ADAPTIVE_THRESH + CALIB_CB_NORMALIZE_IMAGE + CALIB_CB_FAST_CHECK);

The third and fourth parameters are the results of the previous part.

The last two parameters are the results we want to get, which can be brought in after declaration.

The default of other parameters is fine.

So how to get the space attitude of the chessboard after rvecs and tvecs, and what is the attitude coordinate system?

rvecs are rotating vectors, which are transformed into rotating matrices using Rodrigues. The principle of Baidu can be found.

Now that the rotation matrix and translation matrix are obtained, the world coordinates can be obtained according to the calibration formula.
Next, the three-axis rotation angle is solved. The principle is as follows: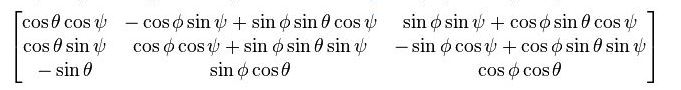

This matrix corresponds to the rotation matrix, from which the Euler angle can be inversely solved.

Ultimately: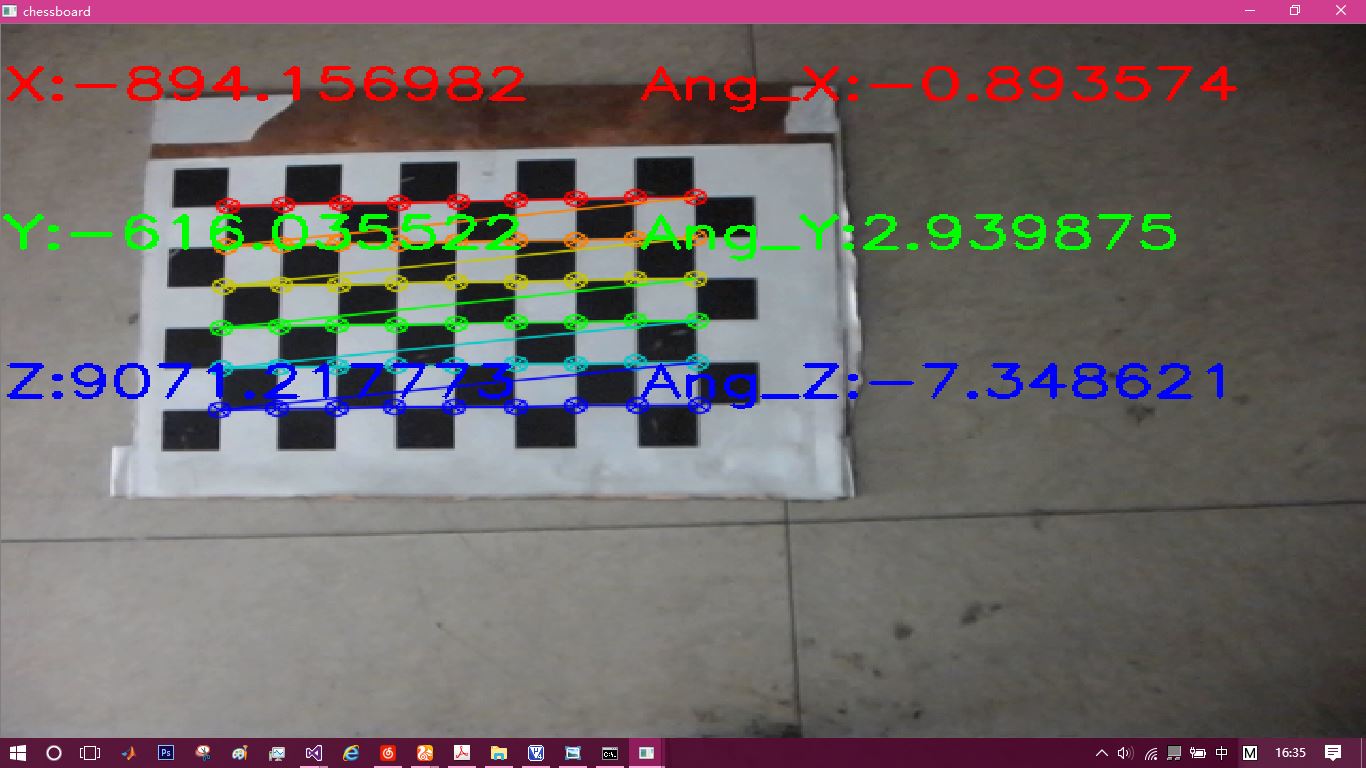

X,Y,Z are the world coordinate units of 0.1mm, ang_X, Y and Z with the lens as the origin. They are the rotation angles of the chessboard along the three axes and the unit degrees.

The code runs in real time with a speed of over 20FPS and a precision of less than 1cm.

Complete code:

#include <cv.h>
#include <highgui.h>
#include <iostream>
#include <math.h>
#define pi 3.14159265358979323846
using namespace std;
using namespace cv;
vector<Point3f> calcBoardCornerPositions(int gridW, int gridH, float squareSize)
{
    vector<Point3f> objectPoints;
        for (int i = 0; i < gridH; i++)
            for (int j = 0; j < gridW; j++)
                objectPoints.push_back(Point3f(float(j*squareSize), float(i*squareSize), 0));
    return objectPoints;
}
vector<Point3f> calcBoardCornerPositions(int gridW, int gridH)
{
    vector<Point3f> objectPoints;
    for (int i = 0; i < gridH; i++)
        for (int j = 0; j < gridW; j++)
            objectPoints.push_back(Point3f(float(j * 89), float(i * 83), 0));
    return objectPoints;
}
int main()
{
    VideoCapture cap(1);
    if (!cap.isOpened()) return -1;
    //cap.set(CV_CAP_PROP_FRAME_WIDTH, 1920);
    //cap.set(CV_CAP_PROP_FRAME_HEIGHT, 1080);
    Mat images, gray;
    Size grids(9, 6);
    int Grids_Size = 260;
    float Ang_X, Ang_Y, Ang_Z;
    float X, Y, Z;
    char key; int i = 0;
    //float A[][3] = { { 644.8137843176841, 0, 302.6526363184274 },{0, 649.3562275395091, 286.5283609342574 },{0, 0, 1 }};
    //float B[] = { 0.01655500980525433, 0.1901812353222618, 0.003461616464410258, 0.002455084197033077, -1.444734184159016 };
    float A[][3] = { { 988.74755, 0, 309.709197 }, { 0, 988.2410178, 239.85705 }, { 0, 0, 1 } };
    float B[] = { -0.41287433, 1.80600373, 0.00250586, 0.0013610796, -7.6232044988 };
    Mat rvecs(3, 1, CV_32F), tvecs(3, 1, CV_32F), cameraMatrix(3, 3, CV_32F), distCoeffs(1, 5, CV_32F), R(3, 3, CV_32FC1);

    for (int i = 0; i < 3; i++)
        for (int j = 0; j < 3; j++)
        {
        cameraMatrix.at<float>(i, j) = A[i][j];
        R.at<float>(i, j) = 0;
        }
    for (int i = 0; i < 5;i++)
    distCoeffs.at<float>(0, i) = B[i];
    namedWindow("chessboard", 0);
    namedWindow("qqq", 0);
    cap >> images;
    while (1)
    {
        cap >> images;
        imshow("qqq", images);
        vector<Point2f> corners;
        bool found = findChessboardCorners(images, grids, corners, CALIB_CB_ADAPTIVE_THRESH + CALIB_CB_NORMALIZE_IMAGE + CALIB_CB_FAST_CHECK);
        if (found) 
        {
            cvtColor(images, gray, CV_BGR2GRAY);
            cornerSubPix(gray, corners, Size(11, 11), Size(-1, -1),
                TermCriteria(CV_TERMCRIT_EPS + CV_TERMCRIT_ITER, 30, 0.1));//0.1 for precision
            drawChessboardCorners(images, grids, corners, found);
            vector<Point3f> objectPoints = calcBoardCornerPositions(grids.width, grids.height, Grids_Size);
            //vector<Point3f> objectPoints = calcBoardCornerPositions(grids.width, grids.height);
            solvePnP(objectPoints, corners, cameraMatrix, distCoeffs, rvecs, tvecs);
            Rodrigues(rvecs, R);

            Ang_X = asin(R.at<double>(1, 0) / cos(asin(-R.at<double>(2, 0)))) / pi * 180;
            Ang_Y = asin(-R.at<double>(2, 0)) / pi * 180;
            Ang_Z = asin(R.at<double>(2, 1) / cos(asin(-R.at<double>(2, 0)))) / pi * 180;

            X = R.at<double>(0, 0) *objectPoints[22].x + R.at<double>(0, 1)  * objectPoints[22].y + R.at<double>(0,2)  * objectPoints[22].z + tvecs.at<double>(0,0);
            Y = R.at<double>(1, 0) *objectPoints[22].x + R.at<double>(1, 1)  * objectPoints[22].y + R.at<double>(1, 2)  * objectPoints[22].z + tvecs.at<double>(1, 0);
            Z = R.at<double>(2, 0) *objectPoints[22].x + R.at<double>(2, 1)  * objectPoints[22].y + R.at<double>(2, 2)  * objectPoints[22].z + tvecs.at<double>(2, 0);
            putText(images, "X:"+to_string(X), { 1, 50 }, 0, 1.0f, CV_RGB(255, 0, 0), 2);
            putText(images, "Y:"+to_string(Y), { 1, 150 }, 0, 1.0f, CV_RGB(0, 255, 0), 2);
            putText(images, "Z:"+to_string(Z), { 1, 250 }, 0, 1.0f, CV_RGB(0, 0, 255), 2);
            putText(images, "Ang_X:" + to_string(Ang_X), { 300, 50 }, 0, 1.0f, CV_RGB(255, 0, 0), 2);
            putText(images, "Ang_Y:" + to_string(Ang_Y), { 300, 150 }, 0, 1.0f, CV_RGB(0, 255, 0), 2);
            putText(images, "Ang_Z:" + to_string(Ang_Z), { 300, 250 }, 0, 1.0f, CV_RGB(0, 0, 255), 2);
            imshow("chessboard", images);
        }
        key=waitKey(20);
        if (key == ' ')
            break;
    }
    return 0;
}

Note that objectPoints[22] in the code is used to calculate the coordinates of the points in the middle of the chessboard. If 0 is used to calculate the coordinates of the first point on the chessboard, this is not important.

Finished.

Next, if you have time, write down the double-purpose. There is also a single target can also use the MATLAB toolbox, the results are similar.